परिधि का त्रिज्या से संबंध

जुई दधीच

पाई का सबसे पहला परिचय वृत्त का क्षेत्रफल निकालने के सूत्र में होता है। यह पाई आया कहां से और उसका मान कैसे निर्धारित किया गया?

सातवीं, आठवीं कक्षा में गणित में वृत्त का क्षेत्रफल ज्ञात करने का सूत्र πx (त्रिज्या)2 सिखाया गया था। यह भी सिखाया गया था कि 7 का मान 3.14 या 22/7 होता है। यहां तक तो ठीक था और ये दोनों बातें दिमाग में फिट हो गईं। किंतु π एक स्थिरांक है ऐसा उस समय शिक्षक ने बताया भी होगा तो भी स्थिरांक का चक्कर तो सिर के ऊपर से ही निकल गया होगा।

मुझे नहीं लगता कि स्थिरांक की अवधारणा आठवीं-नवीं कक्षा के स्तर पर समझाना कोई कठिन काम है, किंतु मेरा अनुमान है कि इसके लिए पर्याप्त समय नहीं दिया जाता। सातवीं, आठवीं तक मेरा दिमाग इतना भोथरा हो गया था कि 'इस की खोज किसने की होगी?', 'किन लोगों के दिमाग में यह कल्पना उभरी होगी?' ‘इसे 7 चिन्ह ही क्यों दिया गया?" ऐसे प्रश्न मेरे मन में उभरे ही नहीं। ऐसा याद नहीं पड़ता कि शिक्षकों से या घर पर कभी इसके बारे में पूछा हो।
वृत्त का क्षेत्रफल = पाई x (त्रिज्या)2 और 1 = 22/7, ये दो बातें पता चल जाने पर वृत्त का क्षेत्रफल ज्ञात करना बहुत ही आसान है, ऐसा उस समय जरूर लगा होगा। किंतु अब गणित पढ़ाना शुरू करने पर 'पाई' के उद्गम के बारे में प्रश्न मन में उठने लगे। अतः इस विषय पर कुछ पढ़ा और उसी का सारांश इस लेख में प्रस्तुत करने का प्रयास कर रही हूं।

पाई का सफरनामा
गणित और विज्ञान के सूत्रों में हमेशा उपयोग में लाए जाने वाले π का इतिहास उतना ही रोचक है जितना मानव का इतिहास। इस इतिहास में एक तरफ आर्किमिडीज़ ने गणितीय अवधारणाओं के आधार पर निकाले π के मान की कहानी है, तो वर्तमान समय में संगणक यानी कम्प्यूटर की सहायता से पाई का शुद्ध मान कैसे ज्ञात किया जाए इसकी समस्या है। इस इतिहास में ईसा पूर्व तीसरी सदी में मिस्र की अलेक्ज़ांड्रिया विद्यापीठ में मानव द्वारा खोजी गई गणित और विज्ञान की मूलभूत अवधारणाओं की गाथा है, तो स्थापित व्यवस्था के खिलाफ उस समय के अनुसंधानकर्ताओं को अपनी बात प्रमाणित करने के लिए किस तरह लड़ाई लड़नी पड़ी, इसकी व्यथा भी है।

हम इस लेख में इतिहास के बिल्कुल शुरुआती दौर से कुछ अधिक पहचान करने वाले हैं। इसके दो कारण हैं। पहला कारण है कि आगे चलकर π का मान ज्ञात करने की विधि का गणित जटिल होता जाता है और दूसरा कि पाठक इस तथ्य से परिचित हो जाएं कि साधारण-सा दिखने वाला π कितनी मुसीबतों से गुज़रा है। इस विषय में अधिक रुचि रखने वालों को और बहुत-सी पठन सामग्री उपलब्ध हो सकती है।
ईसा-पूर्व 2000 तक मनुष्य ने अपने अवलोकनों को सिद्धांत के साथ जोड़कर समानुपात की अवधारणा को स्पष्ट कर लिया था। दो संख्याओं में समान अनुपात होने का अर्थ है कि एक संख्या को दुगनी, तिगुनी, चौगुनी या आधी करने पर दूसरी संख्या भी दुगनी, तिगुनी, चौगुनी या आधी हो जाती है। दो समानुपाती संख्याओं का मान इस तरह कितना ही बढ़ाया जाए, उनके मानों का अनुपात स्थिर रहता है। इस अनुपात को आज हम भाग की क्रिया के द्वारा आसानी से ज्ञात कर लेते हैं, किंतु विशेषज्ञों का मानना है कि पुराने समय में इसे ज्यामिति की सहायता से ज्ञात किया जाता था।

ईसा पूर्व 550 में 'ओल्ड टेस्टामेंट' (बाइबल) में भी आ के अनुपात का उल्लेख है। हिब्रू भाषा की ऊपर लिखी पंक्तियों के अनुसार 'जिसकी परिधि की लंबाई तीन हाथ होती है उसका व्यास एक हाथ लंबा होता है।'

ऐसा प्रतीत होता है कि π की यात्रा समानुपात की अवधारणा से प्रारंभ हुई। वृत्त की परिधि और व्यास में एक निश्चित संबंध होता है, यह गणितज्ञों को पता चल गया था। यह भी स्पष्ट हो गया था कि छोटे से छोटे और बड़े से बड़े वृत्तों की परिधि और व्यास का अनुपात एक ही होता है। फिर यह गणितीय सूत्र बनाया गया। परिधि/व्यास = स्थिरांक। किंतु इस स्थिरांक को π का नाम तो सन् 1800 के बाद ही दिया गया।* पता चला है। कि मिस्र और बेबिलोन के वैज्ञानिकों को इस स्थिरांक, जिसे हम आज π कहते हैं, की जानकारी थी और उन्होंने उसका मान भी पता कर लिया था। बेबिलोन के लोग पाई का मान 31/( 8 ) और मिस्र के लोग 4 x (8/9)2 मानते थे। इस बारे में ठोस जानकारी उपलब्ध नहीं है कि ये मान कैसे प्राप्त किए गए, पर इस संबंध में कुछ अनुमान लगाया जा सकता है।

पाई का मान निकालना
कल्पना कीजिए कि आप गणित में रुचि रखने वाले, ईसा पूर्व 2000 के मिस्र के नागरिक हैं। आजकल प्रयोग की जा रही मापन पद्धति और मापन के साधन आपके पास नहीं हैं। इसलिए कम्पास, कागज़, पेंसिल, आदि के इस्तेमाल का सवाल ही नहीं उठता। आपके पास हैं - केवल रस्सी, लकड़ी की खूटियां और जमीन। अब इस सामग्री के आधार पर पाई का मान पता करेंगे।
सबसे पहले आपने नील नदी के किनारे रेत की एक समतल और सूखी पट्टी ढूंढी। एक स्थान पर लकड़ी की खूटी गाड़ दी और उससे रस्सी बांध कर रस्सी के दूसरे सिरे पर लकड़ी की छोटी, नुकीली खुटी बांध दी। अब आपने रस्सी को कस कर पकड़ा और नुकीली खूटी की सहायता से रेत में

*पाई ग्रीक वर्णमाला का एक अक्षर है। गणित में विभिन्न सूत्रों या राशियों के लिए अलग -अलग ग्रीक अक्षरों को इस्तेमाल करने की प्रथा है। इसी तारतम्य में वृत्त की परिधि और व्यास के अनुपात के लिए पाई का प्रयोग किया जाता है।

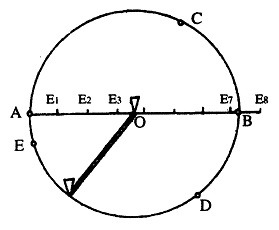पाई का मानः रस्सी और सुंटी की मदद से एक वृत्त खींच लीजिए। उसके बाद एक रस्सी को परिधि पर किसी बिंदु A पर इस तरह रखते हैं कि वह केन्द्र से गुजरती हुई वृत्त की परिधि को B पर छुए। रस्सी का यह टुकड़ा AB काट लेते हैं और फिर इससे परिधि को नापते हैं। रस्सी का टुकड़ा A पर रखने पर पहली बार C तक पहुंचता है, दूसरी बार D तक और तीसरी बार E तक। इस तरह परिधि पर A C D E निशान लगाते जाते हैं। वृत्त की परिधि, वृत्त के व्यास से तीन गुने से कितनी ज्यादा है यह पता करने के लिए हिस्से EA को रस्मी से नापकर उससे AB रेखा पर समान दूरी पर E, Ea, ... निशान लगाते जाइए। चित्र से स्पष्ट है कि इस हिस्से यानी EA रेखा का मान वृत्त के व्यास के 1/7 व 1/8 वें हिस्से के बीच में है। यानी इस विधि से पाई का मान 3(1/7) और 3(1/8)ओके बीच आता है।
एक वृत्त बनाया। वृत्त के केन्द्र पर ठुकी खूटी उखाड़ कर उस छेद को O नाम दिया।
अब रेत पर कुरेदे हुए वृत्त की परिधि पर एक बिंदु A लिया। रस्सी का एक लंबा टुकड़ा लेकर उसके एक सिरे को A पर रखा। रस्सी को इस प्रकार खींचकर रखा कि वह O बिंदु से गुज़रती हुई वृत्त की परिधि पर स्थित अन्य बिंदु B को स्पर्श करे। रस्सी पर AB की लंबाई का निशान कोयले से बना लिया और नुकीले पत्थर से रस्सी को इस निशान तक काट लिया। आज की भाषा में हम इसे वृत्त का व्यास कहते हैं।

अब आपने रस्सी को वृत्त की परिधि पर इस प्रकार रखा कि उसका एक सिरा A पर रहे। जहां रस्सी खत्म हो गई उस स्थान को C नाम दे दिया। दूसरे शब्दों में, वृत्त का व्यास, वृत्त की परिधि के AC भाग पर रखा। अब आपने इसी प्रक्रिया को आगे बढ़ाते हुए रस्सी को C से 2 तक की परिधि के हिस्से पर रखा और तीसरी बार D से E तक के हिस्से पर रखा। वृत्त की परिधि यानी π को तीन बार इस प्रकार नापने पर भी EA भाग बच गया। यानी पाई का मान 3 से कुछ अधिक होगा।

अब इस बचे हुए भाग EA पर विचार करते हैं। पहले आपने इसे रस्सी से नापा। इस नाप EA को व्यास AB पर रखने पर पता चला कि EA, AB के 1/7 वें और 1/8 वें हिस्से के बीच है। आपके इस प्रयोग के अनुसार [ का मान 33 और 34 के बीच होना चाहिए, यानीः
3 (1/8) <π< ( 3 (17)
तो यह था उस π के मान 22/7 का इतिहास जिसे हम स्कूल में शायद ही पढ़ते हैं।
 
उन्नत संस्कृतियां और गणितज्ञ
जहां की भौगोलिक परिस्थिति और वातावरण खेती के अनुकूल थे, वहां लोग बसते गए और संस्कृतियां विकसित होती गईं। सिंधु घाटी और मेसोपोटेमिया (वर्तमान इराक) में भी यही सिलसिला चला। 1936 में मेसोपोटेमिया के प्राचीन शहर बेबीलोन से 200 मील की दूरी पर खुदाई में एक ठीकरा (मिट्टी के बर्तन का टुकड़ा) मिला जिस पर कुछ खुदा हुआ था। पुरातत्व-वेत्ताओं ने अनुमान लगाया कि इसका संबंध ज्यामिति से है।
1950 में भाषाविदों और गणितज्ञों ने मिलकर इसे पढ़ने में सफलता प्राप्त की। इस पर एक सूत्र था। जिसके अनुसार TT का मान 3.125 प्राप्त होता है, जो मिस्र की विधि से प्राप्त किए गए मान से मिलता-जुलता है।
ईसा पूर्व 287 में सायराक्यूज़ (इटली का एक प्राचीन नगर) में जन्मा आर्किमिडीज़ बड़ा ही विलक्षण व्यक्ति था। उसके बारे में अनेक रोचक कहानियां प्रचलित हैं। यह एक अलग मुद्दा है कि उनमें सत्यता का कितना पुट है, किंतु इसमें कोई संदेह नहीं कि आर्किमिडीज़ एक असाधारण प्रतिभा वाला वैज्ञानिक था। π का शुद्ध मान ज्ञात करने का कीड़ा आर्किमिडीज़ के दिमाग में भी घूम रहा था। इसके लिए आर्किमिडीज ने समबाहु बहुभुज आकृतियों के अंतःवृत्त और परिवृत्त का उपयोग किया। ‘मेजरमेन्ट ऑफ ए सर्कल' में आर्किमिडीज़ ने कहा है कि समषद्भुज के स्थान पर समदशभुजा से शुरू करके 6 बार दुगना करके आने वाली संख्या के बराबर भुजाओं वाले समबहुभुज बना कर अंत:वृत्त और परिवृत्त नापने पर 7 का मान 31आता है।
 
सोलहवीं शताब्दी में हॉलैंड के गणितज्ञ लुडॉस्फ हॅन सिलेन ने 7 का शुद्ध मान ज्ञात करने के लिए अपने कार्यकाल का काफी समय खर्च किया और जीवन के अंतिम दिनों में 7 का मान 32 अंकों तक निकाला। उन्होंने भी आर्किमिडीज की विधियों को अपनाया और 2 की 38वीं घात वाले भुजाओं के समबहुभुज के अंत:वृत्त और परिवृत्त की परिधि नापी।
नील और सिंधु नदियों की घाटियों में संस्कृति का विकास लगभग समकालीन था। यही कारण है कि गणित में शोध के क्षेत्र में मिस्र और भारत के निवासियों ने लगभग एक सी उन्नति की। सन् 380 के मिस्र के एक सूत्र में E का मान 3.1416 यानी 3 सही 177/250 दिया गया है। आर्यभट्ट के द्वारा लिखे गए आर्यभटीय में 7 के संदर्भ में उल्लेख हैः ‘सौ में चार जोड़ कर उसे 8 गुना करके उसमें 62000 जोड़ने पर प्राप्त होने वाली राशि 20000 व्यास वाले

कविता से पाई का मान याद रखना

पाई का मूल्य दशमलव के 22वें स्थान तक याद रखना काफी मुश्किल है। किंतु नीचे दी हुई कविता को याद कर लिया जाए तो इसके हर शब्द के अक्षरों की संख्या की सहायता से इसे । याद किया जा सकता है। जैसे हाऊ यानी 3, आई 1, विश 4 ......।

How I wish I could recapture PI - Eureka! cried the great inventor Christmas pudding, christmas pie - is it the problem's very center

यानी पाई का मान होगाः 3.141592653589793223846
इस तरह पाई का मान याद रखने के लिए ऐसे बहुत से तरीके अपनाए जाते हैं।
वृत्त की परिधि होगी' यानी
पाई = 62832/20000
    = 3.1416

भास्कराचार्य के अनुसार भी 7 का उपर्युक्त मान बिल्कुल सही है। विद्वानों की राय है कि भारतीय गणितज्ञों ने भी आर्किमिडीज़ द्वारा अपनाई गई विधियों का ही प्रयोग किया होगा।
19वीं शताब्दी में कई गणितज्ञों ने π का मान 100 अंकों तक, 205 अंकों तक और 607 अंकों तक ज्ञात किया। किंतु कम्प्यूटर से E का मान निकालना एक चुनौती थी। कम्प्यूटर से काम लेने के लिए उसे कम्प्यूटर भाषा में ही निर्देश देने पड़ते हैं। विभिन्न व्यक्तियों ने ऐसे निर्देश तैयार किए। पाई का मान निकालने के लिए जो समीकरण इस्तेमाल किए गए उनमें सबसे अधिक महत्वपूर्ण माना जाने वाला सूत्र/समीकरण भारतीय गणितज्ञ रामानुजन ने 75 वर्ष पहले अपनी कॉपी में लिख रखा था। 1987 में सुपर कम्प्यूटर की सहायता से π का मान 13,42,17,000 अंकों तक कुछ ही घंटों में निकाला गया।
कहा जाता है कि इंसान अपने इतिहास से कुछ समझदारी सीखता है। गणित के इतिहास का तो एक और इस्तेमाल भी है।
अध्यापन के दौरान गणित की अवधारणाओं को बिना उनका इतिहास बताए, बहुत रूखे-सूखे तरीके से बता दिया जाता है। कोई आश्चर्य नहीं कि विद्यार्थियों को गणित एकदम आसमान से टपका हुआ लगता है।
गणित के विषयांशों का अध्यापन करते समय, जहां भी संभव हो, उस अवधारणा के इतिहास से विद्यार्थियों को परिचित करा देना चाहिए। इससे उनके लिए गणित का अध्ययन रोचक बन सकेगा ऐसी आशा की जा सकती है।

पाई का मान निकालने की विभिन्न विधियां

1936 में मेसोपोटेमिया के प्राचीन शहर बेबीलोन से 200 मील की दूरी पर खुदाई में जो ठीकरा मिला उस पर यह सूत्र थाः
समबाहु षट्भुज की परिमाप /समबाहु षट्भुज के परिवृत्त की परिधि = (57/60) + 36(60)²
उस समय बेबीलोन में दाशमिक प्रणाली के स्थान पर 1 से 6 तक गिनती वाली षष्टमान प्रणाली प्रचलित थी। यदि समबाहु षट्भुज की भुजा को r माना जाए और उसके परिवृत्त यानी बाहरी वृत्त की परिधि को c तो ठीकरे पर दिए समीकरण के अनुसार
 6 r/C = (57/60)+36/(60)²

यानी पाई का मान 3.125 प्राप्त होता है जो मिस्र की विधि से प्राप्त किए गए मान से मिलता-जुलता है।
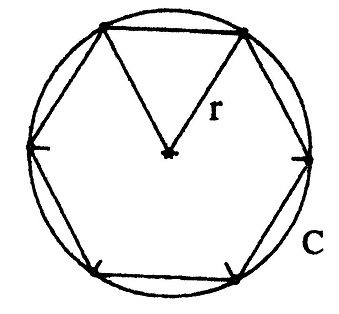
इसके बाद आर्किमिडीज़ ने पाई का मान निकालने के लिए समबाहु बहुभुज आकृतियों के परिवृत्त के साथ-साथ अंत:वृत्त का भी उपयोग किया। जैसा कि साथ दिए गए चित्र से स्पष्ट है। परिवृत्त की परिधि षटभुज के परिमाप से अवश्य अधिक होगी।
अब अगर षट्भुज की प्रत्येक भुजा की लंबाई एक इकाई मान लेते हैं तो ऐसी स्थिति में
परिवृत्त की परिधि > षटभुज का परिमाप
2 π r > C
2 π (1)> 6 या π> 3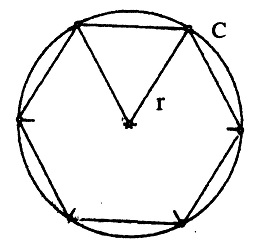

अब अगर षट्भुज के अंदर एक वृत्त अर्थात अंतः वृत्त बना लेते हैं। उसकी परिधि षट्भुज के परिमाप से कम ही होगी। इस अंत:वृत्त की। परिधि पता करने के लिए उसकी त्रिज्या ढूंढनी होगी। अंत:वृत्त की परिधि और षट्भुज की बाहु को छूती हुई समकोण त्रिभुज बनाने पर हम इस वृत्त की त्रिज्या निकाल सकते हैं चूंकि इस समकोण
 
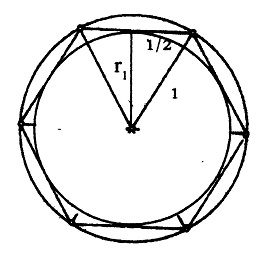त्रिभुज में कर्ण की लंबाई एक है और आधार की लंबाई 1/2 है।
(r₁)² + (1/2)²= 1²
(r₁)² = 1 - (1/4) = 3/4
r₁ = 3/2
इस प्रकार अंत:वृत्त की त्रिज्या का मान 3/2 प्राप्त होता है। अब चूंकि इस अंतः वृत्त की परिधि षट्भुज के परिमाप से कम ही होगी इसलिए
2 πr₁ < c
2 π ( 3/2)< 6
π < 6 / 3
π < 2 3
अब अगर पाई के बारे में परिवृत्त व अंतःवृत्त के आधार पर निकले निष्कर्षों को एक साथ देखें:
तो 3 < π< 2  3
इसके बाद आर्किमिडीज़ ने दुगनी यानी 12 भुजाओं का बहुभुज बनाया। उसके अंत:वृत्त और परिवृत्त की परिमिति नापने पर 3.105 < π< 3.215 मान प्राप्त हुआ। इसी प्रकार चौबीस भुजाओं वाली समबाहु आकृति बनाने पर 3.31 2 < π< 3.1 59 मान प्राप्त हुआ। आर्किमिडीज ने इसी प्रकार 96 समान भुजाओं वाला बहुभुज बनाकर निष्कर्ष निकाला कि 7 का मान 3 सही 10/71 और 3 सही 1/7 के मध्य है और उसका औसत मान 3.14 है। 'मेजरमेन्ट ऑफ ए सर्कल' में आर्किमिडीज ने कहा है कि समषट्भुज के स्थान पर समदशभुजा से शुरू करके 6 बार दुगना करके आने वाली संख्या के बराबर भुजाओं वाले समबहुभुज बना कर अंतःवृत्त और परिवृत्त नापने परπ का मान 3 x (14/16) आता है।

जुई दधीचः सांख्यिकी में पढ़ाई। गणित, शिक्षा और लेखन में रुचि।
अनुवाद: तेजश्री गुप्ते। गणित में स्नातकोत्तर उपाधि, गणित के अध्यापन और लेखन में रुचि।
यह लेख मराठी संदर्भ के अंक-2 ( अक्टूबर-नवंबर 1999) से लिया गया है।