बीजगणित, पायथागोरस और पेपर के टुकड़े

प्रकाश बुरटे

आपने कागज़ से तरह-तरह के गाखिलौने - नाव, हवाई जहाज़, दवात, फूलदान, कौआ आदि बनाने की कभी-न-कभी कोशिश ज़रूर की होगी। इन सब में शुरुआत में जिस भी कागज़ का आयताकार टुकड़ा हो, मोड़ कर उससे वर्ग बनाना होता है। इसके बाद तो आप जो भी बनाना चाह रहे हैं उसके मुताबिक अलग-अलग तरह की आकृतियां बनती जाएंगी।
आयत और वर्ग हमारे आसपास काफी जगहों पर दिखाई देते हैं जैसे - स्कूल या घर की दीवार, छत, कॉपी-किताबें , अखबार-पत्रिकाएं, पोस्टकार्ड, लिफाफे, अलग-अलग आकार के डिब्बों की सतहें ..... यह सूची और बहुत लंबी हो सकती है। हमारी प्रकृति में आयत या वर्ग भले ही बहुतायत में न दिखते हों फिर भी विभिन्न कारणों से इंसान को ये दोनों आकृतियां काफी पसंद हैं।
आयत और वर्ग के चार कोनों में से आमने-सामने वाले दो कोनों को जोड़ने से दो समकोण त्रिभुज प्राप्त होते हैं। आमने-सामने के कोने जोड़ने वाली रेखा यानी आयत और वर्ग और बनने वाले दो त्रिभुजों को कर्ण यानी त्रिभुज भी इंसान द्वारा पसंद किया जाने वाला आकार है ऐसा कहा जा सकता है।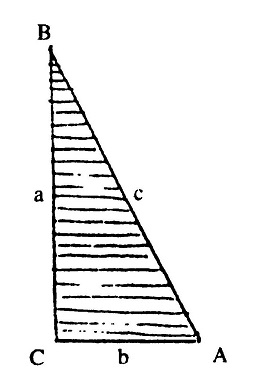
जो भी जानकारी हमें हासिल होती है उससे लगता है कि समकोण त्रिभुज की खासियतों को काफी पहले ही जाना जा चुका था। शुल्बसूत्र में दिए गए उल्लेखों के अनुसार यह कहा जा सकता है कि उत्तर वैदिक काल में ईंटों का उपयोग अनेक प्रकार की यज्ञ वेदियों को बनाने में किया जाता था। वेदियों की रचना में समकोण त्रिभुज की विशिष्टता का उपयोग किया गया होगा ऐसा अनुमान लगाया जा सकता है।
यदि आप समकोण त्रिभुज की विशिष्टता को परखना चाहते हैं तो कागज़, कैंची, स्केल, पेन्सिल व कम्पास बॉक्स लेकर तैयार हो जाइए। कागज़ यदि मोटा हो तो अच्छा अन्यथा गत्ते का उपयोग भी किया जा सकता है। हां, इसे सुगमता से काटने के लिए कैंची या कटर की आवश्यकता होगी। यह एक रोचक खेल है। खेल-खेल में ज्यामिती और बीजगणित के आपसी रिश्ते को भी हम समझ सकते हैं। तो चलिए शुरू करते हैं।
सबसे पहले दो समान आकार के कागज/गत्ते के आयताकार टुकड़े काटिए। आयत के आमने-सामने के दो कोनों को एक सरल रेखा से जोड़ दीजिए। यह रेखा कर्ण कहलाती है। कर्ण के ऊपर से कैंची चलाते हुए आयत को दो टुकड़ों में काटिए। अब आपके पास चार समान आकार के समकोण त्रिभुज उपलब्ध होंगे। इस त्रिभुज को हम ABC त्रिभुज कहेंगे। त्रिभुज की दो भुजाओं की लंबाई क्रमशः a और b होगी तथा कर्ण की लंबाई c होगी,
 
ऐसा हम मान लेते हैं। (चित्र-1)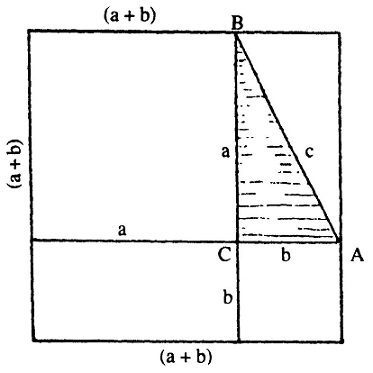
एक अन्य कागज़ पर ABC त्रिभुज को रखकर पेन्सिल से इसकी आकृति बना लीजिए। त्रिभुज की AC व BC भुजाओं को क्रमशः a और b लंबाई के बराबर बढाइए। इन रेखाओं की लंबाई दो दिशाओं में बढ़ा सकते हैं। एक तरह से लंबाई बढ़ाने पर और उसके बाद वर्ग बनाने पर चित्र-2 बनेगा; और दूसरी तरह लंबाई बढ़ाकर काम अंजाम देने पर चित्र-3 मिलेगा।
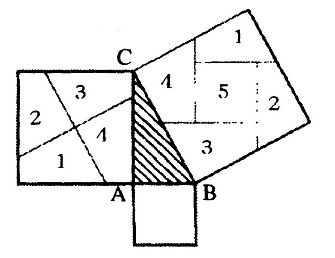
चित्र-2 के आधार पर चित्र4 तैयार कर लीजिए और शुरुआती त्रिभुज की भुजाओं का ख्याल रखकर चित्र-3 को इस्तेमाल करते हुए चित्र-5 बनाना होगा।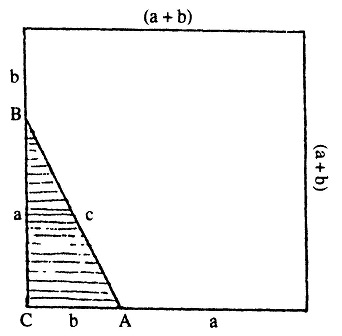
उसके बाद इन दोनों वर्गों को काट लीजिए और एक-दूसरे पर रखकर देखिए कि क्या दोनों वर्ग एक-दूसरे पर एकदम सटीक ढंग से रखे जा सकते हैं। यदि दो आकृतियां एक-दूसरे पर एकदम फिट बैठती हों तो एक बात तो तय हो जाती है कि इन दोनों आकृतियों का क्षेत्रफल समान है। यहां पर इन दोनों वर्गों की भुजाओं की लंबाई a और b के जोड़ के बराबर है इसलिए इनका एक-दूसरे पर सटीक ढंग से रखा जाना अपेक्षा के अनुकूल है।
एक समकोण त्रिभुज की भुजाओं को आगे बढ़ा कर दो वर्ग इस तरह से बनाए कि उनका क्षेत्रफल समान व समकोण त्रिभुज की दोनों भुजाओं के योग के बराबर है। देखिए ऊपर बनाए गए दोनों रेखाचित्र।
 
इन समान क्षेत्रफल के वर्गों में से अलग-अलग तरह से चार समान समकोण त्रिभुज निकाल देने पर हमें पायॉथोगोरस का सूत्र मिल जाता है कि समकोण त्रिभुज के कर्ण पर बने वर्ग का क्षेत्रफल दोनों भुजाओं पर बने वर्गों के योग के बराबर होता है।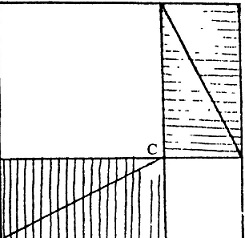

दो वर्ग बराबर तीसरा
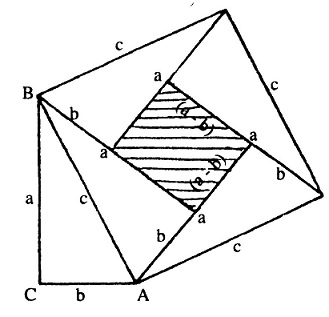
अब इन आकृतियों को ज्यामिति की भाषा में समझने का प्रयास करेंगे। चित्र 4 व 5 में दिखाए वर्गों में एक ही आकार के चार समकोण त्रिभुज समाए हुए हैं (देखें छायांकित त्रिभुज)। यदि चित्र-4 में से छायांकित त्रिभुजों को काटकर अलग किया जाए तो सिर्फ AC और BC इन दो भुजाओं पर दो वर्ग शेष रहते हैं। इनमें से एक वर्ग की भुजा की लंबाई a तथा दूसरे वर्ग की भुजा की लंबाई b है। इसी तरह चित्र-5 से यदि चारों छायांकित त्रिभुज अलग किए जाएं तो कर्ण AC पर एक वर्ग शेष रह जाता है। चूंकि दोनों वर्ग एक समान हैं। इसलिए चित्र 4 व 5 से समान आकार के चार समकोण त्रिभुज हटाने पर दोनों आकृतियों में शेष बचे हिस्सों का क्षेत्रफल समान ही होना चाहिए। अर्थात चित्र-4 में बचे दो वर्गों का कुल क्षेत्रफल चित्र -5 में बचे वर्ग के क्षेत्रफल के बराबर होगा।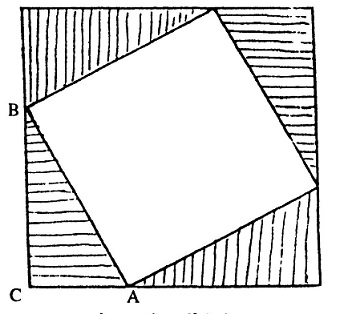
इससे यह अर्थ भी निकाला जा सकता है कि समकोण त्रिभुज की दो भुजाओं पर बने वर्गों के क्षेत्रफलों का योग त्रिभुज के कर्ण पर बने वर्ग के क्षेत्रफल के बराबर होगा। यह पायथॉगोरस का सिद्धांत है जो हम सबने कभी-न- कभी पढ़ा होगा। वैसे मज़े की बात यह है कि समकोण त्रिभुज की दोनों भुजाओं पर बने वर्गों और कर्ण पर बने वर्ग को एक दूसरे पर रखकर इस सिद्धांत की परख नहीं की जा सकती।

अभी तक समकोण त्रिभुज के बारे में जो सूत्र हमने पाया है उसमें हमने त्रिभुज की भुजाओं की लंबाई a और b मानी थी। बीजगणित की भाषा ये कोई भी मूल्य रखने वाले 'चर' (variable) हैं। पायथॉगोरस के सिद्धांत की जांच के लिए युक्लिडीयन ज्यामिति का इस्तेमाल भी किया जा सकता है। अभी तक तो हमने सिर्फ ज्यामितीय आकृतियों को एक-दूसरे पर रखकर उनके आकारों की तुलना और बीजगणित का इस्तेमाल किया है। अब हम ज्यामिति से संबंध न तोड़ते हुए और बीजगणित का थोड़ा ज्यादा उपयोग करते हुए देखते हैं कि हमारे हाथ और क्या-क्या लग सकता है?

ज्यामिति व बीजगणित
आइए शुरुआत चित्र 4 और 5 से करें और देखें कि कि ज्यामितीय आकृतियों के इस खेल में बीजगणित के उपयोग से क्या कोई नया सूत्र हासिल हो सकता है।
-- इन आकृतियों में समकोण त्रिभुज ABC की भुजाओं की लंबाई क्रमशः a और b है।
-- भुजाओं को बढ़ाकर बनाए गए वर्ग की भुजाओं की लंबाई (a + b) है।
-- (a + b) को (a + b) से गुणा करने पर गुणनफल a x a + b x b + a x b + a x b अर्थात a² + b² + 2ab प्राप्त होता है।
-- यहां a² तथा b² क्रमशः भुजा BC तथा AC पर बने वर्गों का क्षेत्रफल दर्शाते हैं।
-- (a x b + a x b) यहां a और b लंबाई की भुजावाले चार समकोण त्रिभुजों का कुल क्षेत्रफल दर्शाता है। - (a+b) x (a+b) भुजाओं को बढ़ाकर बनाए गए बड़े वर्ग का क्षेत्रफल दर्शाता है। बीजगणितीय समीकरण द्वारा इसे निम्नानुसार व्यक्त किया जा सकता
(a+b)² = a²+b²+2ab
a²+b² = (a+b)²- 4(1/2) ab ...... (1)
निष्कर्ष के रूप में हम पाते हैं कि समकोण त्रिभुज की दो भुजाओं a तथा b, पर बने वर्गों के क्षेत्रफलों का योग, (a+b) लंबाई की भुजा वाले वर्ग के क्षेत्रफल में से a व b भुजा वाले चार समकोण त्रिभुजों के क्षेत्रफल को घटाने पर मिलता है। इस बात को हमने चित्र 4 और 5 से बखूबी समझ लिया है।
 
एक और तरीका 
जिस प्रकार बीजगणित में (a+b)² को व्यक्त करने का सूत्र उपलब्ध है। उसी प्रकार (a-b)² को भी सुत्र द्वारा व्यक्त किया जा सकता है: (a-b)² = a² + b² - 2ab या
               a²+b² = (a-b)² + 4(1/2) ab ...... (2)
आइए अब इस समीकरण को ज्यामितीं और कतरन, इन दोनों नज़रियों से देखने की कोशिश करते हैं। इस समीकरण के बाईं ओर का
समकोण त्रिभुज के कर्ण पर बने इस वर्ग में उसी आकार के चार समकोण त्रिभुज हैं और (a-b) भुजा वाला एक छायांकित वर्ग है। बड़े वर्ग का क्षेत्रफल इन हिस्सों के क्षेत्रफल के रूप में लिखने पर हमें समीकरण-2 का दाहिना हिस्सा मिल जाता है।
हिस्सा a²+b² समकोण त्रिभुज की दो भुजाओं पर बने वर्गों के क्षेत्रफलों का योग दर्शाता है। जबकि समीकरण का दाहिनी ओर का हिस्सा a-b लंबाई की भुजा वाले वर्ग तथा चार समकोण त्रिकोणों के क्षेत्रफलों का योग दर्शाता है। समीकरण में '=' का चिन्ह यह दर्शाता है कि समीकरण के दोनों हिस्से बराबर हैं। समीकरण-1 को जिस तरह चित्र 4 और 5 से आसानी से समझाया जा सका, उसी तरह समीकरण-2 को भी कतरनों की ज्यामिति से समझाया जा सकता है।

इसके लिए चित्र-5 से शुरुआत करनी होगी। एक बार फिर कागज़ और कैंची लीजिए और एक अन्य कागज़ पर चित्र-5 बनाइए। इस आकृति के चारों समकोण त्रिभुजों को उनके कर्मों पर से अंदर की ओर मोड़िए - चित्र-6 की तरह। इस आकृति के मध्य में बने छायांकित वर्ग की भुजाओं की लंबाई (a-b) होगी। इस आकृति को ध्यान से देखने पर समीकरण-2 के दाहिने हिस्से के सभी अंग मिल जाएंगे। अर्थात (a-b) भुजा वाला एक वर्ग और a व b भुजाओं वाले चार समकोण त्रिभुज। इस आकृति में स्पष्ट है कि ये चार समकोण व एक छोटा वर्ग मिलकर शुरुआती समकोण त्रिभुज के कर्ण पर वर्ग बना रहे हैं। यानी कि समीकरण-2 का दाहिना हिस्सा इस तरह भी कर्ण पर बनने

वाले वर्ग के बराबर है।
कागज़ की कतरनों के इस खेल से ज्यामिति और बीजगणित में जुड़वां बहन-भाई की तरह के आपसी रिश्ते का बोध होता है। इस गतिविधि को करते हुए यदि किसी के हाथ शुल्बसूत्र से संबंधित कोई किताब लग जाए तो यह बात भी ध्यान में आ जाएगी कि संभवतः यह सिद्धांत तो आर्यों के आगमन से भी पहले का है।

प्रकाश बुरते: आई. आई. टी. मुंबई से पढ़ाई करने के बाद भाभा अनुसंधान केन्द्र में 1998 तक संशोधन कार्य किया और सेवा निवृति ली। शिक्षा में होने वाले नवाचारों के प्रति विशेष रुचि। हाल ही में एकलव्य के साथ जुड़कर महाराष्ट्र की प्राथमिक शालाओं की पाठ्य पुस्तकों की समीक्षा की है।
मूल लेख मराठी में। हिन्दी अनुवादः सुधा हर्डीकरः रसायन विज्ञान की सेवानिवृत प्राध्यापक।