क्रिस्टन हर्बर्ट एवं रेबेक्का एच. ब्राउन [Hindi PDF, 239 kB]
अनुवाद: निदेश सोनी
मैथस्केप: सीइंग एण्ड थिंकिंग मैथेमैटिकली अमेरिका में मिडिल स्कूल गणित के लिए तैयार किया गया एक पाठ्यक्रम था। इसकी देशभर की कक्षाओं में फील्ड-टैस्टिंग हुई। इस पाठ्यक्रम के एक पाठ ‘क्रॉसिंग द रिवर’ में दी गई समस्या का समूहों में बँटे बच्चे हल ढूँढ़ते हुए पैटर्न खोजने की कोशिश करते हैं। यही तो है बीजगणित सोच की शुरुआत।
एक शिक्षक ने अपनी कक्षा छठवीं के बच्चों को ‘patterns in Number and shapes’ (संख्याओं और आकारों में पैटर्न) इकाई के एक पाठ ‘क्रॉसिंग द रिवर’ का बच्चों के साथ परिचय कराने के लिए एक कहानी बनाई।
“तुम और तुम्हारा एक साथी, 8 वयस्कों के साथ एक लम्बी सैर पर पैदल निकले हैं। सब बहुत थक चुके हैं। तुम सब एक चौड़ी नदी के किनारे पहुँचते हो, और घर जाने के लिए तुम सबको उस नदी को पार करना ही होगा। परन्तु तुम्हारे समूह में कोई भी तैरना नहीं जानता। नदी के किनारे एक छोटी नाव है, जिसमें एक बार में केवल 2 बच्चे या 1 वयस्क, या फिर 1 बच्चा ही जा सकता है। तुम्हारे दल के सभी लोगों को नदी पार कराने के लिए नाव के कितने चक्कर लगाने पड़ेंगे?”
कक्षा में इस कहानी पर एक संक्षिप्त चर्चा के बाद विद्यार्थियों के समूहों ने इस समस्या को सुलझाने के लिए कई तरीके अपनाए। कुछ समूहों ने कागज़ पर रेखाचित्र बनाकर शुुरुआत की। कई ने इस पर अभिनय किया। कुछ ने विभिन्न रंगों के घनाकार गुटकों के साथ यह करके देखा कि नदी को पार करने के लिए कितनी बार जाना होगा। उनकी रणनीति जो भी हो परन्तुु हर समूह के बच्चे एक खोजी प्रक्रिया का सहारा ले रहे थे, जो उन्होंने पैटर्न ढूँढ़ने एवं उनके सामान्यीकरण करने के दौरान सीखी थी। और साथ ही वे बीजगणितीय सोच की नींव का निर्माण कर रहे थे।
संख्याओं और आकारों में पैटर्न पर इकाई को राष्ट्रीय विज्ञान संस्थान के अनुदान से निर्मित पाठ्यक्रम मैथस्केप: सीइंग एण्ड थिंकिंग मैथेमैटिकली के अन्तर्गत विकसित किया गया था, और पूरे देश की कक्षाओं में इसकी फील्ड-टैस्टिंग हुई थी। इसके प्रत्येक पाठ में विद्यार्थियों को एक ऐसी समस्या का सामना करना पड़ता है जो सन्दर्भ के साथ दी जाती है। इस समस्या पर काम करने के लिए वे जोड़ियों या छोटे समूहों में काम करते हैं। इस पर बच्चे अभिनय करके, गतिविधि करके या चित्र बनाकर, अथवा वास्तविक चीज़ों के साथ कुशलतापूर्वक जोड़-तोड़ करके पेश की गई स्थिति का खाका बनाकर काम करते हैं। बच्चे समस्या को सुलझाने के लिए खोजी प्रक्रिया को अपनाते हैं:
* वे कहानी में एक पैटर्न को खोजते हैं,
* वे पैटर्न को पहचानकर विभिन्न विधियों के उपयोग से उसका विवरण देते हैं, और
* वे पैटर्न का सामान्यीकरण करते हैं और कहानी से उसका सम्बन्ध जोड़ते हैं।
‘संख्याओं और आकारों में पैटर्न’ की इकाई एवं पाठयक्रम की अन्य बीजगणित केन्द्रित इकाइयाँ यहाँ पर एक नई धारणा देने का प्रयास करती हैं कि बच्चे कैसे बीजगणितीय सोच की दक्षताओं को विकसित कर सकते हैं। विद्यार्थियों को वास्तविक जीवन में बीजगणित के उपयोग और उसके औचित्य को दिखाने के लिए बीज-गणितीय सोच का यह व्यापक दृष्टिकोण लिया गया है। गणितीय चिन्हों एवं साधनों के उपयोग के साथ विभिन्न परिस्थितियों का विश्लेषण कर पाना बीजगणितीय सोच है जिसमें,
* दी गई परिस्थिति से सूचना निकाल पाना, जैसे कि यहाँ प्रस्तुत परिस्थिति है - ‘नदी पार करना’,
* प्राप्त हुई सूचना को शब्दों, रेखाचित्रों, तालिका, ग्राफ और समीकरण में प्रदर्शित करना, और
* उसी स्थिति एवं नई सम्बन्धित स्थिति में प्राप्त गणितीय जानकारी को समझना एवं व्याख्या करना, जैसे कि अज्ञात के लिए हल करना, अनुमान को परखना और कार्यात्मक सम्बन्धों की पहचान करना।
‘संख्याओं और आकारों में पैटर्न’ की इकाई में, उपयोग में आने वाली यह खोजी प्रक्रिया, तीन भागों वाले ढाँचे का एक प्रारम्भिक एवं अनौपचारिक उदाहरण है (चित्र-1)।
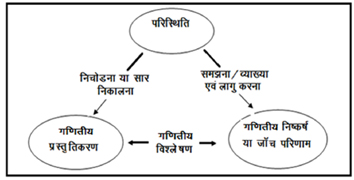
चित्र-1: सन्दर्भ आधारित बीजगणितीय सोच का एक ढाँचा
सन्दर्भ के साथ दी गई समस्या को इस खोजी प्रक्रिया के उपयोग से हल करने पर यह बच्चे को बीजगणित के अनौपचारिक खोज के मौके प्रदान करती है, जिसकी चर्चा ‘स्कूल गणित के पाठयक्रम और मूल्यांकन मानकों’ में की गई है। यह कहता है - “तो कक्षा 5 से 8 तक के विद्यार्थियों के लिए यह आवश्यक है कि वे अनौपचारिक तरीकों से बीजगणितीय अवधारणाओं की खोज करें जिससे वे आने वाली बीजगणित की औपचारिक पढ़ाई के लिए बुनियाद निर्मित कर सकें।” यह इकाई बच्चों के द्वारा सीखी गई बीजगणितीय सोच को उनके अपने शब्दों और अपने संकेतों में बताने पर ज़ोर देती है, न कि बच्चों को औपचारिक सांकेतिक बीजगणित की ओर ढकेल दिया जाए। साथ ही पाँच सप्ताह की यह इकाई विद्यार्थियों को इस बात के लिए सहायता और अवसर देती है कि वे पैटर्न तलाशने की दक्षता और ठोस परिस्थितियों में पैटर्न के सामान्यीकरण करने की क्षमता को विकसित कर सकें। इस पद्धति में यह भी निहित है कि बीजगणित के एक सक्षम विद्यार्थी होने का बच्चों का आत्मविश्वास स्वयं में बढ़े।
समस्याओं के हल के लिए खोजी प्रक्रिया
खोजी प्रक्रिया में मूलत: तीन चरण होते हैं: (1) पैटर्न खोजना, (2) पैटर्न पहचानना, और (3) सामान्यीकरण करना। ये तीन चरण चित्र-1 में दिखाए गए ढाँचे के विशिष्ट घटक हैं; पैटर्न खोजना सूचना या सार निकालना है, पैटर्न की पहचान करना गणितीय विश्लेषण है, और सामान्यीकरण करना मतलब जो सीखा है उसकी व्याख्या करना एवं लागू करना है। बच्चे इस इकाई के सभी 12 पाठों में इस खोजी प्रक्रिया का अनुसरण करते हैं। इस लेख में एक पाठ ‘नदी पार करना’ को उदाहरण के रूप में इस्तेमाल करके बच्चे जिस खोजी प्रक्रिया का अनुसरण करते हैं, उसको चित्रित किया गया है। बच्चे स्टुडेंट-शीट (विद्यार्थियों के लिए छपा पन्ना, चित्र-2) से मार्गदर्शन लेते हैं। शिक्षकों की एक गाइड में समस्या को हल करने में बच्चों की मदद के लिए मेनिप्युलेटिव (गणित सिखाने के लिए कुछ मूर्त चीज़ें एवं तरीके), भौतिक गतिविधि (फिज़िकल एक्टिविटी) और डायाग्राम या रेखाचित्र बनाने के सुझाव बताए गए हैं।
पैटर्न खोजना
‘नदी पार करना’ समस्या के हल की शुरुआत के लिए बच्चे इस परिस्थिति (चित्र-2, चरण-1) का एक मॉडल तैयार करते हैं और पहले कदम के रूप में पैटर्न को तलाशते हैं। जैसा कि शिक्षक गाइड में सुझाव दिया गया है, शिक्षक बच्चों को कुछ कांउटर (गिनती के लिए कुछ चीज़ें) -- जिससे इस समस्या को सुलझाने में मदद मिले -- देंगे; एक जैसे रंग के दो कांउटर बच्चों को प्रदर्शित करते हैं और दूसरे रंग के आठ कांउटर वयस्कों को प्रदर्शित करते हैं (चित्र-3)।
जैसे ही बच्चे नाव को नदी के एक किनारे पर लाकर वापस चलाना प्रारम्भ करते हैं, तो वे टिप्पणियाँ करना शु डिग्री कर देते हैं। जैसे कि - “किसी को तो नाव को वापस लेकर जाना होगा, क्या एक बच्चा यह कर सकता है” और “इन बच्चों के हाथ तो नाव चलाने के बाद सचमुच बहुत थक जाएँगे।”
|
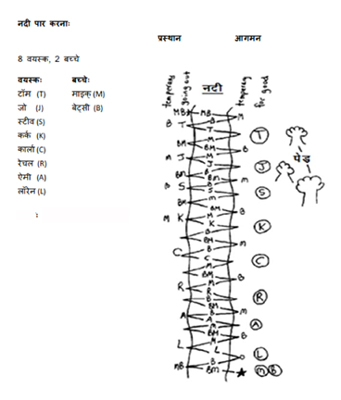
1. एक समूह जिसमें 8 वयस्क और 2 बच्चे हैं, एक नदी को पार करना चाहता है। वहाँ एक नाव है जिसमें एक बार में केवल 1 वयस्क, या 1 बच्चा, या 2 बच्चे जा सकते हैं। सभी नाव को चला सकते हैं। सभी को नदी पार करने के लिए नाव को कितनी बार नदी पार करनी होगी? |
चित्र-2: ‘नदी पार करना’ के लिए विद्यार्थियों का पन्ना
बच्चे इस समस्या पर काम करने के दौरान आँकड़ों को संग्रह एवं दर्ज करते हैं। वे आँकड़ों को दर्ज करने के लिए कई विधियों को विकसित करते हैं। कुछ बच्चे नाव के चक्करों को दर्ज करने के लिए सूची में टेली चिन्हों (खड़े, आड़े या अन्य निशान) का प्रयोग करते हैं, और कुछ बच्चे चित्र या रेखाचित्र बनाकर नदी पार करने के लिए लगने वाले प्रत्येक चक्कर को दिखाते हैं (देखें चित्र-3)। जब बच्चे अपने आँकड़ों को संग्रहित व दर्ज कर रहे थे तो वे बार-बार आने वाले (दोहराव वाले) पैटर्न पर ध्यान देना शु डिग्री करते हैं, कुछ बच्चों को मूर्त वस्तुओं के साथ काम करते समय पैटर्न दिखाई देता है और पैटर्न को जाँचने के लिए वे उनके द्वारा दर्ज किए गए आँकड़ों को देखते हैं।
उदाहरण के लिए, एक कक्षा में दो लड़कियों ने अपनी शिक्षिका से कहा, “हमने पैटर्न ढूँढ़ लिया।” मूर्त सामग्री का उपयोग करके, उन्होंने अपनी शिक्षिका को दिखाया और बताया, “पहले आप दो बच्चों को भेजेंगे, इसके बाद एक बच्चा वापिस आएगा, तब उसके बाद हम एक वयस्क को भेजेंगे, अब दूसरा बच्चा नाव को लेकर वापिस आएगा, इस बात से कोई फर्क नहीं पड़ता है कि हमारे पास कितने वयस्क है, हमें बस दो बच्चे चाहिए होंगे। आप किसी भी संख्या में वयस्कों को ले जा सकते हैं भले ही उन्हें पार करने में पूरा दिन लग जाए।” यह बताने के लिए कि 8 वयस्कों के लिए कितनी पारी लगानी होंगी, ये दोनों लड़कियाँ वापिस करके देखने लगीं। उन्होंने सभी पारियों को दर्ज किया, और इसके बाद सभी यात्राओं को गिना। अन्य बच्चे अपने द्वारा दर्ज किए गए आँकड़ों में पैटर्न को तलाश रहे थे, (2 बच्चे गए, 1 बच्चा वापिस आया, 1 वयस्क गया, दूसरा बच्चा वापिस आया, 2 बच्चे गए, 1 बच्चा वापिस आया और इसी तरह) और उन्होंने पहचाना कि 1 वयस्क के साथ नदी पार करने में चार चक्कर लगाने होंगे।
पैटर्न पहचानना
बच्चों ने अलग-अलग वयस्कों की संख्या के साथ ऐसी कई अन्य समस्याओं को हल करने की कोशिश की (चित्र-2 का चरण-2)। कुछ बच्चों के लिए अतिरिक्त समस्याओं को हल करना उनकी पैटर्न की समझ को जाँचने एवं परिष्कृत करने का एक रास्ता था (देखें चित्र-4)। और अन्य बच्चों के लिए यह पैटर्न पहचानने का एक अतिरिक्त अवसर था (देखें चित्र-5)।
|
जब मैं प्रक्रिया को चरण के अनुसार कर रहा था, मैंने किया, और मैंने पाया कि मैं दोहरा रहा हूँ। इसने मुझे पैटर्न को देखने में मदद की। हर बार चार स्टेप के बाद फिर उसी चीज़ को कर रहा था, लगातार बार-बार, तब मैंने वयस्कों की संख्या को 4 से गुणा किया और अपना उत्तर पा लिया। और इसका सूत्र है, |
इस चरण की अन्तिम समस्या के रूप में बच्चों से यह ढूँढ़ने के लिए कहा गया कि 100 वयस्कों को नदी पार कराने के लिए कितने चक्कर लगाने होंगे। इस बार कुछ बच्चों ने उत्तर पाने के लिए सामग्री का इस्तेमाल नहीं किया, बल्कि इसके स्थान पर उन्होंने अपने पैटर्न की समझ में दूसरी संख्या के स्थान पर 100 को रखकर गणना की और उत्तर निकाला (देखें चित्र-5)।
|
आपको बस इतना करना है कि वयस्कों की संख्या में 4 का गुना करना है, और फिर उस नियम का उपयोग करते हुए 1 जोड़ना है, जिसकी बात हमने स्कूल में की थी। |
हालाँकि कुछ बच्चे मूर्त संसाधनों का प्रयोग करते हुए समस्या को इस बिन्दु तक हल कर रहे थे। एक बच्चे की दुविधा उसी की टिप्पणी में दिखाई देती है, “पेपर में यह कहा गया था कि यदि 100 वयस्क होंगे तो उत्तर क्या होगा। और मैं सोच रहा था कि अब हमें 100 वयस्कों के लिए यह प्रश्न हल करना पड़ेगा। मैं आशा करता हूँ कि हमें यह प्रश्न नहीं करना होगा।” बच्चों से बहुत बड़ी संख्या में वयस्कों को पार करवाने की समस्या को हल करने के लिए कहना उन्हें प्रेरित करता है कि वे समस्या के हल के लिए एक व्यापक विधि की ओर रुख करें जो पैटर्न पर आधारित हो, जिसे उन्होंने हर समस्या में देखा है और उसे बड़ी संख्याओं वाली समस्याओं के साथ भी लागू किया जा सकता है।
बच्चे पैटर्न के सामान्यीकृत कथन की खोज के लिए आँकड़ों को विविध तरीकों से उपयोग व प्रस्तुत करते हैं। अगर बच्चे कहीं फँस जाते हैं तो शिक्षिका उन्हें सलाह दे सकती है कि वे अपने आँकड़ों को तालिका या ग्राफ में प्रदर्शित करें। इस इकाई के शुरुआती पाठों में बच्चों को तालिका एवं ग्राफ से आँकड़े पढ़ना सिखाया जाता है, ऐसा प्रस्तुतिकरण पैटर्न तलाशने में मदद कर सकता है।
व्यापीकरण
समस्या के अन्तिम चरण में (चित्र-2 में चरण-3) बच्चे प्रत्येक सदस्य को नदी पार कराने के लिए कितनी पारी लगानी होंगी के लिए एक सामान्यीकृत विधि विकसित करते हैं, वयस्कों की दी गई किसी भी संख्या के लिए। बच्चे अपने साथी को एक स्पष्ट सामान्यीकृत नियम उस रूप में बताते हैं जिसमें वह सबसे ज़्यादा सहज हो - शब्दों के प्रयोग से, चित्रों से, उनके खुद के द्वारा बनाए चिन्हों से, या समीकरण के ज़रिए - और इसे वे मौलिक परिस्थिति के साथ जोड़ते हुए बताते हैं (चित्र 5 एवं 8)।
बच्चों के लिए इस चरण का सबसे महत्वपूर्ण पहलू यह बताना है कि उनका यह सामान्यीकरण कैसे भौतिक स्थितियों से सम्बद्ध है, आप क्यों वयस्कों की संख्या को 4 से गुणा कर रहे हैं? और अन्तिम चक्कर के लिए 1 क्यों जोड़ रहे हैं? जब बच्चे इन प्रश्नों का उत्तर देने लगते हैं, उन्होंने एक महत्वपूर्ण समझ को पाया है कि कैसे बीजगणितीय सोच को ठोस परिस्थिति के मॉडल के रूप में उपयोग किया जा सकता है।
पैटर्न के सामान्यीकरण से बच्चे बीजगणितीय सोच की ताकत को समझ पाते हैं। जैसे एक बच्चे ने कहा - “वहाँ एक पैटर्न था, प्रत्येक चार चक्करों का समूह एक जैसा था। आप सूत्र के द्वारा यह पता लगा सकते हैं कि कितनी पारियाँ लगेंगी। तेज़ी से पता लगाने के लिए आप सूत्र का प्रयोग कर सकते हैं।” एक अन्य बच्चे ने लिखा, “मैंने सोचा कि हमें सूत्र ढूँढ़ना चाहिए तो समस्या को हल करना ज़्यादा आसान हो जाएगा। सूत्र, समस्या को हल करना आसान बना देता है। यह बहुत मददगार था।” तीसरे बच्चे ने लिखा, “कभी-कभी जब आप यह सोचते हैं कि आपको एक समीकरण मिल गया है, आपने सच में क्या पाया है, वह कदम जिससे आप समस्या को छोटे रास्ते से हल कर सकें।” जब बच्चों के सामने मिलती-जुलती परिस्थितियाँ प्रस्तुत की जाती हैं, तो वे बीजगणितीय सोच की इस ताकत को देखकर प्रेरित होते हैं और इस दिशा में प्रयास करते हैं।
इस पद्धति पर एक पूरी इकाई के लाभ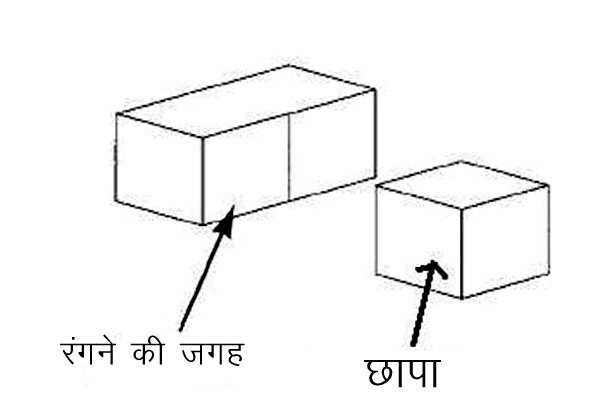
जैसे कि ‘नदी पार करना’ एक उदाहरण है, इसी इकाई में और पाठ भी इसी पद्धति (तरीके) का इस्तेमाल करते हैं। बच्चों को एक सन्दर्भ-आधारित समस्या दी जाती है, जिसे उनको एक खोजी प्रक्रिया के द्वारा हल करना होता है। उदाहरण के लिए, ‘रंगी हुई छड़ें’ में बच्चों से कहा जाता है कि एक कम्पनी विभिन्न लम्बाइयों की रंगी हुई छड़ एक रंग छापने वाली मशीन से बनाती है (देखें चित्र-7)। एक समय में मशीन से एक छड़ पर रंग काएक वर्गाकार छापा लगता है। बच्चों से पूछा जाता है कि, “विभिन्न लम्बाई की छड़ों की सभी सतहों को रंगने के लिए कितनी बार छापे लगाने पड़ेंगे?” खोजी प्रक्रिया का अनुसरण करते हुए बच्चों ने सामग्री का उपयोग किया एवं छड़ों के प्रतिरूप का निर्माण किया। बच्चे एक अकेले वर्गाकार घन को रंग के छापे की तरह प्रयोग करते हैं, जिससे वे 1 से लेकर 10 तक की लम्बाई की छड़ों को भौतिक रूप से जाँच पाएँ या सोच कर दिमागी छवि बना पाएँ। जैसे ही बच्चों ने इन छड़ों की समस्या को हल किया, उन्होंने आँकड़ों को दर्ज किया, उन्हें एक तालिका में व्यवस्थित किया, और वे इस तालिका का प्रयोग संख्याओं में पैटर्न ढूँढ़ने के लिए करने लगे।
अगले काम के रूप में बच्चों ने 12, 25 और 100 इकाई लम्बाई की छड़ों को रंग करने के लिए ज़रूरी छापों की संख्या पता लगाई। 100 लम्बाई की छड़ जैसी बड़ी संख्या की समस्या को हल करने के लिए बच्चे छड़ों की लम्बाई और रंग करने के लिए ज़रूरी छापों की संख्या के सामान्यीकृत सम्बन्ध को खोजने के लिए प्रेरित हुए। बच्चों ने इसके लिए अपनी पसन्द की विधि चुनी - शब्द, रेखाचित्र या उनके खुद के बनाए हुए चिन्ह - जो एक नियम की तरह उनके पैटर्न की सामान्यीकृत समझ को प्रदर्शित कर सके। और अन्तत: बच्चों ने मौलिक परिस्थिति के सन्दर्भ में अपने नियम को प्रस्तुत किया।
|
नियम यह है कि हमेशा 1 वयस्क को पार कराने में 4 एक तरफ की पारियाँ लगेंगी। तो आपको वयस्कों की संख्या में 4 गुणा करके अपने उत्तर में 1 जोड़ना चाहिए। आप 1 जोड़ते हैं क्योंकि बच्चों का उपयोग वयस्क के साथ होता है। अत: 100 वयस्कों के साथ आपको यह करना चाहिए 100 बार 4 और + 1 |
अपनी सोच को बढ़ावा देने के लिए बच्चे सोचने लगते हैं कि दिए गए परिणाम (आउटपुट) को प्राप्त करने के लिए उन्हें क्या करना (इनपुट देना) होगा। उदाहरण के लिए ‘रंगी हुई छड़’ में बच्चों से कहा गया कि वे अपनी पैटर्न की समझ का उपयोग करके इस प्रश्न को खोजें - “यदि छड़ को रंगने में 86 छापे लगते हैं तो छड़ कितनी लम्बी होगी?” एक और तरीका जिससे बच्चे की सोच बढ़ती है, उनसे इसी तरह के परन्तु अधिक कठिन सवाल पूछने का है। उदाहरण के लिए ‘नदी पार करना’ के पूरे होने के बाद बच्चों से उसी तरह की समस्या को अलग-अलग बच्चों की संख्या के साथ करने के लिए कहा गया। “पैटर्न का क्या होगा, यदि हमारे पास बच्चों की संख्या भिन्न हो? (अ) 8 वयस्क और 3 बच्चे (ब) 2 वयस्क और 5 बच्चे?” वैसे ही ‘रंगी हुई छड़ें’ के बाद बच्चों से दुगनी लम्बाई वाली छड़ों की समस्या को हल करने के लिए कहा जा सकता है। साथ ही संख्याओं एवं आकारों में पैटर्न की इकाई का पाठ बच्चों को पैटर्न तलाशने, पैटर्न पहचानने और सामान्यीकृत करने की खोजी प्रक्रिया को सीखने के विविध अवसर प्रदान करता है। बच्चे प्रत्येक पाठ में इस प्रक्रिया से जूझते हैं और फलस्वरूप इस इकाई के पूरे होते-होते वे उन स्थितियों जिनमें पैटर्न उपस्थित हैं, को हल करने की पद्धति को समावेशित (इन्टर्नलाइज़) कर लेते हैं। प्रक्रिया उपयोग करने की रणनीति में प्रत्यक्ष है, तालिका, ग्राफ और मौखिक नियम जिनका उपयोग वे पैटर्न बताने में करते हैं, और सामान्यीकृत नियम जिसे वे स्पष्ट रूप से बताते हैं। अब यदि उनके सामने भविष्य में पैटर्न से जुड़ी कोई समस्या आएगी तो उनके पास उस समस्या को सुलझाने के लिए रणनीति होगी।
इस इकाई का एक और सकारात्मक प्रभाव ठोस परिस्थिति पर एक नियम को सामान्यीकृत करने की बच्चे की अनुभूति की क्षमता पर है, जो है, बीजगणितीय रूप से सोच पाना। जैसे-जैसे बच्चे प्रक्रिया का अनुसरण करते हैं, वे पैटर्न को ढूँढ़ने में सक्षम हो जाते हैं, और उसे एक सामान्यीकृत नियम की तरह व्यक्त करते हैं। एक बच्चा लिखता है - “सूत्र को निकालना रोमांचक है। यह किसी पुरातत्ववेता को पुरावशेष मिलने के समान है।” किसी सूत्र को खोज पाना बच्चों को सफल महसूस कराता है, और इसके परिणाम स्वरूप वे खुद को बीजगणित के एक सक्षम विद्यार्थी की तरह देखते हैं। शिक्षक जिन्होंने इस इकाई को (क्षेत्र परीक्षण में) पढ़ाया था ने बयान किया कि - “बच्चे आत्मविश्वासपूर्ण हैं, उन्हें लगता है वे अच्छा कर रहे हैं।” “उन्हें लगता है कि वे स्मार्ट हैं। वे जानते हैं कि उनके बड़े भाई व बहन बीजगणित करते हैं।” बच्चों की बीजगणितीय सोच में लगे रहने की क्षमता से बढ़ता आत्मविश्वास निश्चित ही बीजगणित के प्रति उनके सकारात्मक नज़रिए को बनाने में योगदान देता है। उनके सकारात्मक नज़रिए का, उनकी खोजी प्रक्रिया के उपयोग और उनकी बीजगणितीय सोच की नई ताकत के साथ संयोजन कक्षा छठवीं के बच्चों को एक मज़बूत आधार देता है, जिस पर वे समस्त माध्यमिक कक्षाओं के दौरान अपनी बीजगणित की औपचारिक समझ का निर्माण कर सकते हैं।
क्रिस्टन हर्बर्ट: पिछले कई वर्षों से एजुकेशन डेवलपमेंट सेंटर (ईडीसी) में पाठयक्रम बनाने का काम कर रही हैं। उनकी खास रुचि बीजगणित एवं बच्चों के आकलन में है।
रेबेक्का एच. ब्राउन: रेबेक्का ब्राउन ईडीसी में एक कक्षा शोधकर्ता हैं। उनकी खास रुचि बीजगणित एवं तकनीक में है। कक्षा में शोध के इस कार्य को जारी रखने की उनकी योजना है।
दोनों ही लेखक उन सभी शिक्षकों एवं बच्चों के बहुत आभारी हैं, जिन्होंने इस इकाई का क्षेत्र परीक्षण किया। वे ईडीसी के अपने सहकर्मियों की भी आभारी हैं जिन्होंने इस इकाई को बनाने में सहयोग दिया, और साथ ही चार्ल्स लोविट की भी जिन्होंने इस इकाई के कई प्रश्नों का प्रारम्भिक स्वरूप तैयार किया।
अँग्रेज़ी से अनुवाद: निदेश सोनी एवं गणित समूह, एकलव्य।
यह लेख ‘Algebrain thinking , Grades K-12:Reading from NCTM's school- based journal and other publication ( Reston,Va: National Council of Teacher of Mathematics,2000)pp 123-28' से लिया गया है।
