सुमित कुमार
भिन्न प्राथमिक कक्षाओं की एक महत्वपूर्ण अवधारणा है। भिन्न, प्राथमिक स्तर में पढ़ रहे छात्र-छात्राओं की संख्याओं की समझ का विस्तार करता है जिससे वे ऐसी मात्रा को संख्या या शब्दों के रूप में निरूपित कर सकें, जो पूर्ण (continuous whole and discrete whole) नहीं हैं। जो लोग बच्चों को पढ़ाने के काम में लगे हैं वे बखूबी जानते हैं कि बच्चों में भिन्न की मात्रात्मक समझ विकसित कर पाना कितना मुश्किल है। इस लेख में कुछ अनुभव साझा कर रहा हूँ जो मैं अपनी कक्षा में, बच्चों के साथ काम करते हुए समझ पाया हूँ।
अज़ीम प्रेमजी फाउंडेशन, उत्तरकाशी में काम करते हुए कई विद्यालयों में जाने का अवसर प्राप्त हुआ। इन विद्यालयों में बच्चों से गणित विषय पर बातचीत करते हुए मैंने अनुभव किया कि भिन्न, गणित की उन अवधारणाओं में से एक है जो बच्चों को बड़ी मुश्किल भरी दुनिया में ले जाती है। इस समस्या के कारणों को समझने के लिए जब मैंने बच्चों की भिन्न की समझ और इस समझ के निर्माण के लिए अपनाए गए तरीकों एवं दिए गए अवसरों को देखा तो पाया कि बच्चों को भिन्न समझाने के लिए जो तरीके अपनाए गए हैं, वे अपूर्ण और समस्या का मुख्य कारण हैं।
मैंने पाया कि बच्चों की भिन्न की समझ इस परिभाषा तक सीमित हो गई है।
दूसरे शब्दों में हम कह सकते हैं कि बच्चों के लिए भिन्न केवल श्याम-पट्ट या कॉपी पर बने कुछ बराबर हिस्सों में बँटे अमूर्त चित्र और उनमें छायांकित भाग को अंकों में लिखने तक सीमित है। कहीं-कहीं पेपर फोल्डिंग का भी उपयोग किया जाता है। मगर ये उपयोग केवल श्यामपट्ट पर बने, कुछ बराबर हिस्सों में बँटे अमूर्त चित्र को सिर्फ मूर्त रूप देता नज़र आता है।
बच्चों को ऐसे अवसर बहुत ही कम मिलते हैं जिनमें वे भिन्न का उपयोग कर ऐसी मात्रा, जो पूर्ण नहीं है, उसे संख्या या शब्दों में व्यक्त कर सकें और पूर्ण के साथ उसके सम्बन्ध को समझ पाएँ। इस परिभाषा से इतर जब आप भिन्न की अवधारणात्मक समझ पर कोई सवाल करते हैं तो बच्चों को मुश्किल में पाते हैं।
उदाहरण के लिए मेरी कक्षा में की गई एक गतिविधि साझा कर रहा हूँ।
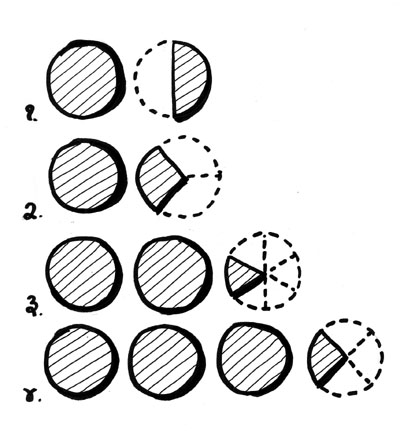
मैंने कक्षा छह और सात के बच्चों को चार समूह में बाँट दिया। पहले समूह को एक पूरा और एक आधा कटा वृत्ताकार कागज़ दिया। दूसरे समूह को एक पूरा और एक, एक-तिहाई कटा वृत्ताकार कागज़। तीसरे समूह को दो पूरे और एक उस वृत्ताकार कागज़ का छठवाँं भाग दिया। इसी प्रकार चौथे समूह को तीन पूरे और एक, एक-चौथाई कटा वृत्ताकार कागज़ दिया।
सभी से बोला गया, “आप बारी-बारी से बिना कागज़ दिखाए पूरी कक्षा को बताएँ कि आपके समूह को कितना वृत्ताकार कागज़ दिया गया है। ताकि बाकी समूह के साथियों को स्पष्ट रूप से पता चल सके कि किस समूह के पास कितनी मात्रा में वृत्ताकार कागज़ है।” मेरे द्वारा किए गए हर अगले सवाल के बाद बदलते उत्तर और उसके लिए बच्चों के द्वारा अपनाई गई प्रक्रियाओं को देखते हुए भिन्न से जुड़े कुछ महत्वपूर्ण बिन्दुओं पर बात करेंगे। चारों समूह का पहला उत्तर इस प्रकार था:
* प्रथम - एक पूरा और एक आधा।
* दूसरा - एक पूरा और एक आधा।
* तीसरा - दो पूरे और एक आधा।
* चौथा - तीन पूरे और एक आधा।
आधा यानी क्या?
इस उत्तर से यह तो स्पष्ट था कि अधिकांश बच्चों को आधे की समझ नहीं थी। उन्हें यह स्पष्ट नहीं था कि आधा, दो में से किसी भी एक ऐसे टुकड़े को कहते हैं, जो लिए गए पूर्ण को दो बराबर हिस्सों में बाँटने पर प्राप्त होता है। यह भी कह सकते हैं कि अधिकांश बच्चों को यह समझ नहीं थी कि दो आधे, लिए गए पूर्ण को पूरी तरह ढँक लेते हैं। जबकि श्यामपट्ट पर बने चित्र को देखकर वे बड़ी आसानी से लिख पा रहे थे। यह भी हो सकता है कि आधे के अलावा अन्य टुकड़ों को व्यक्त करने के लिए उनके पास शब्द ही न हों।
मैंने कहा, “पहले दो समूहों के उत्तर से तो लगता है कि दोनों समूह के पास बराबर वृत्ताकार कागज़ होने चाहिए।” सभी बच्चों ने कहा, “हाँ।” फिर दोनों समूह को कहा गया कि वे अपने वृत्ताकार कागज़ सभी बच्चों को दिखाएँ और बताएँ कि क्या दोनों समूह के पास बराबर वृत्ताकार कागज़ हैं।
लगभग सभी बच्चों ने कहा, “बराबर नहीं हैं।”
दूसरा सवाल -- यह कैसे पता चला कि इन दो समूह के पास बराबर वृत्ताकार कागज़ नहीं हैं? उत्तर आया कि एक तो पूरा वृताकार कागज़ दोनों समूह के पास है और पहले समूह का टुकड़ा दूसरे समूह के टुकड़े से बड़ा है।
एक-दूसरे के ऊपर रखकर देखना
मैंने पूछा, “यह कैसे पता चला कि दूसरे समूह का टुकड़ा छोटा है?”
कुछ देर के बाद आवाज़ आई, “दोनों को एक-दूसरे के ऊपर रखकर देख लो।”
एक और सवाल पहले समूह से पूछा गया, “कैसे पता चला कि यह आधा है और इसी पूर्ण (whole) का आधा है?” पहले समूह के सभी बच्चे कुछ देर तो चुप रहे, फिर एक बच्चे ने कहा, “इस पूर्ण को बीच से मोड़ो तो इस टुकड़े के जैसा दिखाई पड़ता है और एक-दूसरे को पूरी तरह ढँक लेता है।”
यहाँ पर भिन्न से जुड़ी एक महत्वपूर्ण दक्षता (ढँक कर मापने) की सहायता लेते हुए निम्न दो बातों पर ज़ोर दिया जाना चाहिए।
पहली, बच्चों को अवसर दिया जाना चाहिए कि वे एक जैसे बराबर कटे टुकड़े से पूर्ण को ढँक (overlap) कर देखें और इस निष्कर्ष तक ले जाने की कोशिश करनी चाहिए कि अगर एक जैसे दो टुकड़े पूर्ण को ढँक रहे हों तो ये टुकड़े दिए पूर्ण का दूसरा भाग हैं और इन्हें आधा भी कहते हैं। इसी प्रकार अगर एक जैसे तीन टुकड़े पूर्ण को ढँक रहे होंे तो ये टुकड़े दिए पूर्ण के तीसरे भाग हैं और इन्हें एक-तिहाई भी कहते हैं।
दूसरी बात, इस बात पर ज़ोर दिया जाना चाहिए कि ये टुकड़े इस पूर्ण को पूरी तरह ढँक रहे हैं, इसलिए ये इस पूर्ण के आधे या एक-तिहाई हैं, न कि किसी अन्य वृत्ताकार कागज़ के। दो आधे टुकड़े देकर, कुछ अलग-अलग आकार के वृत्त में से पूर्ण ढूँढ़ने की गतिविधि भी की जा सकती है।
मैंने कहा, “पहले समूह ने तो स्पष्ट रूप से बता दिया कि उनके पास एक पूरा वृत्ताकार कागज़ और एक ऐसा टुकड़ा है, जो उस पूरे वृत्ताकार कागज़ को दो बार में पूरा-पूरा ढँक लेता है, जिसे हम आधा भी कहते हैं।” पहले समूह की इस बातचीत के बाद अन्य समूहों ने अपने उत्तर में परिवर्तन करना चाहा।
अब उत्तर इस प्रकार थे।
दूसरा समूह - एक पूरा और एक टुकड़ा।
तीसरा समूह - दो पूरे और एक टुकड़ा जो आधे से छोटा है।
चौथा समूह - तीन पूरे और एक टुकड़ा।
टुकड़ा यानी क्या?
मैंने बच्चों से पूछा, “क्या सिर्फ टुकड़ा कहने से यह स्पष्ट हो रहा है कि किसके पास कितना बड़ा टुकड़ा है या फिर दूसरे समूह के पास आधे से कितना छोटा टुकड़ा है?” बच्चों ने जवाब दिया, “नहीं।” मैंने पूछा, “फिर क्या कर सकते हैं कि आपके कहने मात्र से सबको स्पष्ट रूप से पता चल जाए कि आपके पास कितना बड़ा टुकड़ा है, अगर सबको पूर्ण वृत्ताकार कागज़ के आकार के बारे में जानकारी है?”
कुछ समय और लेने के बाद तीसरे समूह और चौथे समूह ने फिर से अपने उत्तर में परिवर्तन किया। अब उत्तर इस प्रकार थे।
तीसरा समूह - दो पूरे और एक छठवाँ भाग।
चौथा समूह - तीन पूरे और चार टुकड़े।
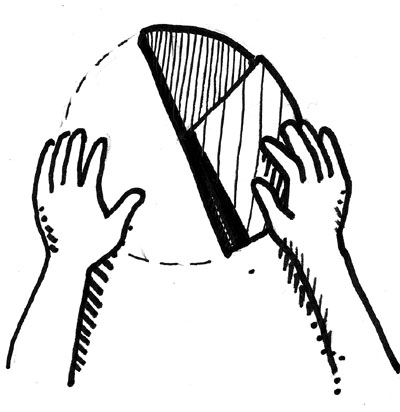मैंने तीसरे समूह से पूछा, “आप उत्तर तक कैसे पहुँचे?” जवाब आया, “हमने इस टुकड़े को पूर्ण के ऊपर रखना शु डिग्री किया और पेंसिल से चिन्ह लगाते गए। अन्त में हमने पाया कि ऐसे छह टुकड़े, दिए गए पूर्ण वृत्ताकार कागज़ को ढँक रहे हैं। इसलिए यह छठवाँ भाग है।”
मैंने कहा, “बिलकुल सही है।”
चौथा समूह अपने उत्तर के करीब था, पर थोड़ी-सी कोई उलझन अभी भी थी। मैंने पूछा, “क्या आपके पास चार टुकड़े हैं?” समूह के सारे बच्चे आपस में फिर कुछ और चर्चा करने लगे। इस बीच दूसरे समूह में भी कुछ बातें चल रही थीं। थोड़ी देर बाद चौथे समूह के एक बच्चे ने कहा, “हमारा टुकड़ा ऐसा है कि अगर ऐसे ही चार टुकड़े हों तो पूर्ण पूरा ढँक जाएगा।” तीसरे समूह में से किसी ने तुरन्त कहा, “चौथा भाग।”
मैंने कहा, “आपके पास तीन पूरे और एक, एक-चौथाई वृत्ताकार कागज़ हैं।” इसी प्रकार बाकी समूहों की मदद से दूसरा समूह भी अपने सही उत्तर तक पहुँच गया था।
हम लोगों ने अक्सर देखा होगा कि बच्चे जिस प्रकार प्राकृतिक संख्या का अपने जीवन में पूर्ण मात्रा (whole quantity) का बोध करने के लिए उपयोग करते नज़र आते हैं, उतनी ही सरलता से भिन्न संख्याओं का उपयोग ऐसी मात्रा, जो पूर्ण नहीं है, का बोध करने के लिए नहीं कर पाते हैं। श्यामपट्ट और कॉपी पर बन रहे चित्र शायद वे अवसर नहीं दे पा रहे हैं कि बच्चे पूर्ण को पूरा ढँकने, और टुकड़े का पूर्ण के साथ सम्बन्ध समझ पाएँ। पूर्ण को पूरा ढँकने का इस्तेमाल केवल पूर्ण के साथ हो सकता है। उदाहरण के लिए आयताकार, वर्गाकार या वृत्ताकार कागज़। जब हमारा पूर्ण कई सम्पूर्ण वस्तुओं का समूह हो, उदाहरण के लिए 12 सेब, 18 पेन इत्यादि, तब बच्चे पूर्ण को टुकड़े से ढँककर तो नहीं देख सकते।
मगर एक बार अवधारणा स्पष्ट हो जाए, तब 3 सेब के समूह के लिए यह कहना कि -- ऐसे चार समूह लिए गए पूर्ण ‘12 सेब के समूह’ के बराबर होंगे, इसलिए 3 सेब लिए गए पूर्ण का चौथा हिस्सा या एक-चौथाई हैं -- बच्चों के लिए बहुत कठिन नहीं होता है।
ये दो अवधारणाएँ, बच्चों में भिन्न की अन्य अवधारणाओं जैसे कि समतुल्य भिन्न और भिन्न की संक्रियाओं की, अवधारणात्मक समझ बनाने में भी बहुत मदद करती हैं।
सुमित कुमार: अज़ीम प्रेमजी फाउण्डेशन, उत्तरकाशी में दो वर्षों से स्कूली शिक्षण में गणित विषय में कार्य कर रहे हैं। गणित शिक्षण में हो रहे नवाचारों को जानने और समझने में रुचि।
सभी चित्र: अंकिता ठाकुर: राष्ट्रीय डिज़ाइन संस्थान, अहमदाबाद से ग्राफिक डिज़ाइन में स्नातकोत्तर की पढ़ाई कर रही हैं। बाल साहित्य और चित्रों में दिलचस्पी रखती हैं।