किसी ने ¼ लिख दिया इससे यह साफ नहीं होता कि भिन्न की उसकी समझ पुख्ता है। बल्कि थोड़ा गहराई में उतरने की कोशिश करें - यह जानने की कोशिश करें कि ऊपर लिखे एक का क्या मतलब है, नीचे लिखा चार क्या बताता है, तो समझ आता है कि लोग कहां फंस जाते हैं।
हाल ही मैंने अपने दो साथियों के साथ एक कार्यशाला में भाग लिया। इसमें भाग लेने वाले लोग होशंगाबाद जिले के केसला ब्लॉक के आसपास के गांवों के थे। आठवीं से दसवीं पास ये युवा अपने गांवों के सरकारी स्कूलों में बतौर पूरक शिक्षक पढ़ा रहे थे।
इस दौरान उनके साथ कई और मुद्दों के अलावा भिन्न की समझ पर भी बातचीत हुई। साथ ही हमने यह भी समझने का प्रयास किया कि भिन्न अवधारणा को कैसे स्पष्ट किया जाए।
गणित के सत्र में जैसे ही हमने ‘भिन्न क्या है, भिन्न से आप क्या समझते हैं?' जैसा सवाल उठाया कि चुप्पी छा गई। जब उनको बहुत कुरेदा तो एक शिक्षक ने जवाब दिया, “भिन्न में दो संख्याएं होती हैं जो एक रेखा के द्वारा एक-दूसरे से अलग होती हैं। इनमें ऊपर वाली संख्या को अंश तथा नीचे वाली संख्या को हर कहते हैं।'' इस शिक्षक के अलावा कहीं और से कोई जवाब नहीं आया। यानी चुनौती हमारे लिए भी थी - भिन्न को कुछ ऐसे तरीके से समझा पाना कि सभी उसे समझ सकें।
आम और बस आम...!
हमारी उनसे जो बातचीत हुई वह कुछ इस प्रकार थी :
“मान लीजिए आपके पास चार आम हैं और आपको इन्हें दो लड़कों में बराबर-बराबर बांटना है, तब आप क्या करेंगे?"
"दोनों को दो-दो आम दे देंगे।''
"यदि दो आमों को दो आदमियों में बांटना है तब प्रत्येक को कितने आम मिलेंगे?"
“प्रत्येक को एक-एक आम।'' - "और यदि एक आम को दो लोगों में बांटना है तब प्रत्येक को कितना हिस्सा मिलेगा?''
“आधा-आधा आम।" -
"यह आधा क्या है? इसे अंकों में ब्लैकबोर्ड पर लिखकर दिखाओ।''
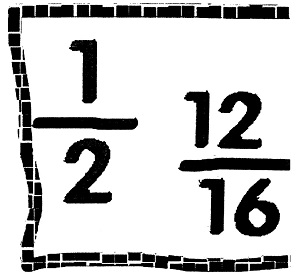
कक्षा में फिर सन्नाटा छाया। बहुत जोर देने पर उनमें से एक ने ब्लैकबोर्ड पर आकर 1/2 लिख दिया। इन्हीं से हमने पूछा, “यह क्या है?"
“आधा है।''
"किसका आधा?''
“एक आम का।'' “एक आम के कितने हिस्से किए?"
"दो हिस्से।'' - ‘दो ही हिस्से क्यों किए?"
"क्योंकि दो लोगों में बांटना है।''
"यानी जितने लोगों में बांटना है उतने हिस्से करने होंगे न?"
“हां।''
"ठीक है। अब बताओ ब्लैकबोर्ड पर दो कहां लिखा है?"
उसने ब्लैकबोर्ड पर लिखे 1/2 के उस हिस्से की ओर इशारा किया जहां 2 लिखा था। हमने कहा ठीक है अब आप इस दो के पास लिखो ‘कुल हिस्से।
फिर हमने पूछा, “प्रत्येक व्यक्ति को कितना हिस्सा मिलेगा।'' उसने कहा, “एक हिस्सा।'' हमने कहा, “अब इस 1 के पास लिखो, जितने हिस्से मिलना हैं।"
अब सूत्र बन गयाः 1
1/2 यानी जितने हिस्से मिलना है।/कुल हिस्से
अब हमने पूछा, “इस सूत्र को देखकर बताओ यदि एक आम आठ लोगों में बांटना है तो प्रत्येक को कितना हिस्सा मिलेगा?"
इस प्रश्न पर फिर सन्नाटा छा गया। हमें लगा कि सीधे पूछने की बजाए बात को शायद इस तरह रखने से काम बने। हमने उनसे पूछा, “अच्छा एक बात बताओ यदि आठ लोगों में बांटना हैं तो कुल कितने हिस्से करने होंगे?"
“आठ हिस्से।"
“तब कुल हिस्से की जगह 8 लिखो।''
एक शिक्षक ने बोर्ड पर एक लाइन खींची और 'हर' के स्थान पर 8 लिख दिया।
“अब चूंकि ये आठ हिस्से आठ लोगों में बांटने हैं तो प्रत्येक को कितना हिस्सा मिलेगा?"
"एक-एक हिस्सा।"
"तब जहां लिखा है ‘जितने हिस्से मिलना है वहां 1 लिख दो।''
तब उसने अंश में 1 लिख दिया।
हमने कहा, “अब इस पूरी संख्या को पढ़ो।"
उन्होंने पढ़ा, “एक बटे आठ।”
हमने कहा, “बिलकुल सही, एक बटे आठ का मतलब होता है कोई चीज जो आठ बराबर भागों में बांटी है उनमें से एक हिस्सा।''
फिर हमने पूछा, “अच्छा अब बताओ एक आम को तीन लोगों को बराबर-बराबर बांटा तो प्रत्येक को कितना हिस्सा मिलेगा?"
उनमें से एक ने ब्लैकबोर्ड पर आकर पहले एक लाइन खींची। फिर हर के स्थान पर 3 लिखा और सूत्र देखा फिर कुछ सोचकर अंश में 1 लिखकर कहा, “एक बटा तीन।"
इसके बाद हमने इसी तरह के और भी उदाहरण देकर उनसे अभ्यास करवाए। हमें लगा बात उनकी समझ में आ रही है। पर एक मजेदार बात देखने में आ रही थी कि अब हम किसी भी भिन्न जैसे 1/2, 13, 1/4 ..... के बारे में पूछते तो वे लोग कहते “एक आम के दो बराबर हिस्सों में से एक", “एक आम के तीन बराबर हिस्सों में से एक"... यानी वे किसी भी भिन्न को बिना आम के समझने की कोशिश ही नहीं कर रहे थे। गोया भिन्न न हुआ आम का बाग हो गया।
जब हमने पूछा, “एक बोरा गेहूं के बीस बराबर हिस्से किए और उसमें से 1/20 भाग रामू को दे दिया तो बताओ 1/20 का मतलब कितना हुआ?"
उन्होंने कहा, “एक आम के बीस बराबर भागों में से एक हिस्सा।'' इस घटना को देखकर हमें समझ आया कि एक ही तरह की चीज़ के उदाहरण देने की प्रवृति से हमें भी बचना चाहिए। इसके बाद हमने अलग-अलग चीजों का उदाहरण लेते हुए उन सभी भिन्नों को फिर से दोहराया।
कुछ और भिन्न
अभी तक तो हमने साधारण भिन्न की ही बात की थी जिसमें अंश की
संख्या 1 थी। अब उन भिन्नों की बात करनी थी जिनके अंश की संख्या 1 से ज्यादा यानी 2, 3, 4... आदि हो। इस बार हमने पहले वाले सूत्र में थोड़ा सुधार करके उसे इस तरह लिखाः
जितने हिस्से मिलना है x 1/कुल हिस्से
उदाहरण के लिए मान लो आपके पास 4/5 आम है तो इसे कुछ इस तरह से लिखेंगे -
4 x 1/5
इसका मतलब यह होगा की एक आम के पांच बराबर भाग किए और उन पांच हिस्सों में से चार हिस्से आपने लिए तो आपका कुल हिस्सा हुआ 4/5
इसी तरह 5/8 को हम निम्न प्रकार से समझ सकते हैं।
5 x 1/8
इसे पढ़ेंगे, पांच गुणा एक बटे आठ। इसका मतलब है एक चीज़ के आठ बराबर भाग । किए। अब इन आठ बराबर हिस्सों में से एक हिस्सा जितना हो, उसका 5 गुना (यानी ऐसे पांच हिस्से मिलकर पांच बटा आठ बनेंगे)।
इसी प्रकार कई और उदाहरण देखे जा सकते हैं। जैसे - किसी चीज़ के चार बराबर हिस्से करने पर जितना एक हिस्सा हो ऐसे तीन भाग मिलकर 3/4 बनेगा।
उसके बाद हमने कहा इन सभी उदाहरणों में तुम एक बात तो स्पष्ट देख सकते हो कि भिन्न में हमेशा बराबर भाग ही शामिल होते हैं।
4/5 और 5/4 में फर्क 
अब दो संख्याओं पर गौर करते हैं। - 1/5 और 5/1 अब तक हुई चर्चा के अनुसार 4/5 का मतलब होता है। किसी चीज के 5 बराबर भाग करो और उनमें से चार भाग ले लो। इसी तरह से सोचें तो 5/4 का मतलब क्या होगा?
उनमें से एक ने उठकर कहा
“किसी चीज़ के चार बराबर भाग करो और उनमें से 5 भाग ले लो।'' बोलने के बाद उसे खुद अपनी ही कही हुई बात गलत लगी। उसने कुछ सोच कर कहा - "नहीं नहीं ... पांच में से चार ... नहीं ... चार में से पांच .... नहीं मुझे नहीं पता। आप बताओ 5/4 का मतलब क्या है।''
हमने कहा, “तुमने पहले जो कहा वह सही है। बस, कहने का तरीका अलग है। दरअसल 5/4 का मतलब है। किसी चीज के चार बराबर भाग किए, और वे चारों भाग लेने के साथ-साथ - उतनी ही बड़ी वैसी ही एक और चीज के फिर चार बराबर हिस्से किए और - उनमें से भी एक हिस्सा ले लिया। इस तरह तुमने कुल 5 हिस्से लिए। ये प्रत्येक पांच हिस्से बराबर हैं और प्रत्येक हिस्सा उतना ही है जितना उस चीज़ को चार बराबर भागों में बांटने पर एक भाग होगा।"
4/5 और 5/4 में से 4/5 को समझना आसान है क्योंकि 5 हिस्सों में से 4 हिस्से लेना समझ में आता है परंतु 5/4 में लगता है कि यहां कुछ अलग तरह की बात उभरकर आ रही है। यहां 5/4 अनुचित भिन्न और 4/5 उचित भिन्न कहलाते हैं।
हमने उनसे कहा, “इन संख्याओं को देखते हुए उचित और अनुचित भिन्न की क्या पहचान बता सकते हो।'' शायद उन्हें हमारा प्रश्न समझ नहीं आया। हमने फिर पूछा, “यदि तुम्हें ढेर सारे भिन्न दिए गए हों और उनमें उचित और अनुचित भिन्न छांटना हो तब तुम उन्हें कैसे पहचानोगे?"
इस बार फिर सन्नाटा r गया। फिर हमने कहा, अच्छा 4/5 और 5/4 में क्या अंतर है?'' किसी ने बताया, “एक में 4 ऊपर 5 नीचे और दूसरी में 5 ऊपर व 4 नीचे है।''
हमने पूछा, “अच्छा 4 और 5 में से छोटी संख्या कौन-सी है?'' जवाब आया, "4"
तब हमने कहा, “अच्छा अब 4 की जगह छोटी संख्या व 5 की जगह बड़ी संख्या लिखकर बताओ।'' उन्होंने वैसा ही किया। हमने कहा, “अब इनमें से 4/5 के सामने उचित, 5/4 सामने अनुचित भिन्न लिखो।'' उन्होंने लिखाः
4/5 छोटी संख्या/बड़ी संख्या उचित भिन्न
5/4 बड़ी संख्या/ छोटी संख्या अनुचित भिन्न
यानी मोटे तौर पर हम उचित भिन्न और अनुचित भिन्न को इस तरह से समझ सकते हैं, कि जिन भिन्नों में अंश की संख्या हर की संख्या से छोटी होती है वे संख्याएं उचित भिन्न कहलाती हैं और जिन भिन्नों में अंश की संख्या हर की संख्या से बड़ी होती है वे अनुचित भिन्न कहलाती हैं।
5/4 समझने का एक और तरीका
अनुचित भिन्नों को एक और तरीके से भी समझाया जा सकता है। इसके लिए फिर से 5/4 पर विचार करते हैं।
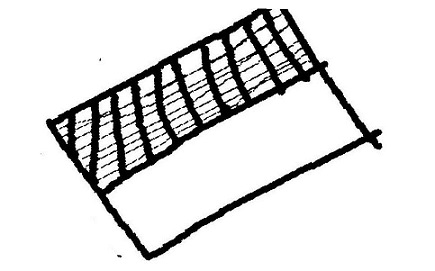
5/4 का मतलब है किसी चीज़ के चार बराबर भाग किए, और वे चारों भाग लेने के साथ-साथ - उतनी ही बड़ी वैसी ही एक और चीज़ के फिर चार बराबर हिस्से किए और - उनमें से भी एक हिस्सा ले लिया। इस तरह कुल 5 हिस्से लिए। छायांकित भाग उस हिस्से को दिखा रहा है जो आपने लिया है।
चूंकि पहले चार हिस्सों में से चारों हिस्से ले लिए तो हमारे बनाए गए सूत्र के अनुसार इसे हम लिखेंगे - 4/4
और दूसरे चार हिस्सों में से 1 हिस्सा लिया तो हमारे सूत्र के अनुसार, इसे लिखेंगे - 1/4
इस तरह अपने कुल 4/7 + 1/4 हिस्से लिए।
अब 4/4 = 1 होता है क्योंकि एक चीज़ के चार बराबर भागे करके चारों ही भाग ले लेने का मतलब है एक पूरी चीज़ ले ली। इसलिए अब उपरोक्त संख्या को हम निम्न प्रकार भी लिख सकते हैं
1¼ - इसे एक सही एक बटा चार पढ़ते हैं।
इस तरह के भिन्नों को मिश्रित भिन्न कहते हैं।
एक सही एक बटा चार का मतलब है 1 पूरा और दूसरा एक चौथाई। इसी तरह 3½ का मतलब है, पूरी वस्तुएं और एक आधी वस्तु।
छाया दुबेः एकलव्य द्वारा प्रकाशित स्रोत फीचर सेवा में कार्यरत हैं।
