विवेक मेहता
[Hindi PDF, 184 kB]
बल सम्बन्धित अध्याय में हम अक्सर बलों को किन्हीं दिशा-विशेष में विघटित करके देखते हैं - अक्सर X एवं Y निर्देशांकों में। इस लेख में रस्साकशी के उदाहरण से शुरु करते हुए यह समझने की कोशिश है कि जब दो से ज़्यादा बल एकदम विपरीत दिशा में न लग रहे हों तो उनका कुल परिणाम समझने व पता करने के लिए यह एक उपयोगी विधि है। थोड़ा-बहुत गणित ज़रूर इस्तेमाल करना पड़ता है, परन्तु बहुत ही बुनियादी स्तर पर।
 रस्साकशी एक बेहद ही मज़ेदार खेल है। शायद आपने कभी खेला या देखा हो। रस्सी का एक छोर पकड़े हुए एक टीम, दूसरे छोर की टीम को अपनी ओर खींचने की कोशिश करती है। ज़ाहिर-सी बात है कि जब मुकाबला हो ज़ोर-आज़माइश का, तो वही टीम जीतेगी जिस टीम के खिलाड़ी ज़्यादा ज़ोर से रस्सी को खींच पाएँगे। लेकिन अगर दोनों टीम बराबर ज़ोर लगाएँ तब क्या होगा? कुछ भी नहीं, रस्सी और दोनों टीम अपनी-अपनी जगह पर यथावत बने रहेंगे। न कोई टीम जीतेगी, न कोई टीम हारेगी। और यांत्रिकी (मेकेनिक्स) की भाषा में हम कहेंगे कि रस्सी पर लगने वाले दो बलों की यह व्यवस्था सन्तुलन में है। इस सन्तुलित व्यवस्था के साथ हम कुछ प्रयोग कर सकते हैं। लेकिन उससे पहले हम ज़रा रस्सी व उस पर लगने वाले बलों की इस विशेष-सी लगने वाली व्यवस्था को एक साधारण रूप में व्यक्त कर लेते हैं ताकि दो बलों की ऐसी किसी भी व्यवस्था को समझा जा सके।
रस्साकशी एक बेहद ही मज़ेदार खेल है। शायद आपने कभी खेला या देखा हो। रस्सी का एक छोर पकड़े हुए एक टीम, दूसरे छोर की टीम को अपनी ओर खींचने की कोशिश करती है। ज़ाहिर-सी बात है कि जब मुकाबला हो ज़ोर-आज़माइश का, तो वही टीम जीतेगी जिस टीम के खिलाड़ी ज़्यादा ज़ोर से रस्सी को खींच पाएँगे। लेकिन अगर दोनों टीम बराबर ज़ोर लगाएँ तब क्या होगा? कुछ भी नहीं, रस्सी और दोनों टीम अपनी-अपनी जगह पर यथावत बने रहेंगे। न कोई टीम जीतेगी, न कोई टीम हारेगी। और यांत्रिकी (मेकेनिक्स) की भाषा में हम कहेंगे कि रस्सी पर लगने वाले दो बलों की यह व्यवस्था सन्तुलन में है। इस सन्तुलित व्यवस्था के साथ हम कुछ प्रयोग कर सकते हैं। लेकिन उससे पहले हम ज़रा रस्सी व उस पर लगने वाले बलों की इस विशेष-सी लगने वाली व्यवस्था को एक साधारण रूप में व्यक्त कर लेते हैं ताकि दो बलों की ऐसी किसी भी व्यवस्था को समझा जा सके।

इन दो बलों की व्यवस्था को समझने के लिए चित्र-1 में दिखाए अनुसार हम मान सकते हैं कि एक टेबल पर एक बिन्दु O है और इस बिन्दु की एक तरफ, टेबल के सपाट तल में, F1 बल लग रहा है व पहले बल की दिशा के विपरीत F2. रस्साकशी से तुलना करें तो F1 एक और F2 दूसरी टीम के द्वारा लगाया गया बल है। बिन्दु O रस्सी पर कोई भी एक बिन्दु हो सकता है। आसानी के लिए हम यह भी मान लेते हैं कि बल F1 बिन्दु T1 से पूर्व की ओर लग रहा है और F2 बिन्दु T2 से पश्चिम की ओर। अब जैसा कि हमने देखा, अगर F1=F2 होगा तो बिन्दु O की टेबल पर स्थिति ज्यों की त्यों बनी रहेगी। अगर F1 या F2 में से कोई भी दूसरे की तुलना में ज़्यादा हुआ तो बिन्दु O उस बल की दिशा में खिसकता चला जाएगा। खैर, इन दो बलों का मान जो भी हो बिन्दु O हमेशा T1 व T2 को जोड़ने वाली रेखा पर ही रहेगा और सिर्फ उस पर ही नज़र रखकर हम यह बता सकते हैं कि तंत्र सन्तुलित है या नहीं।
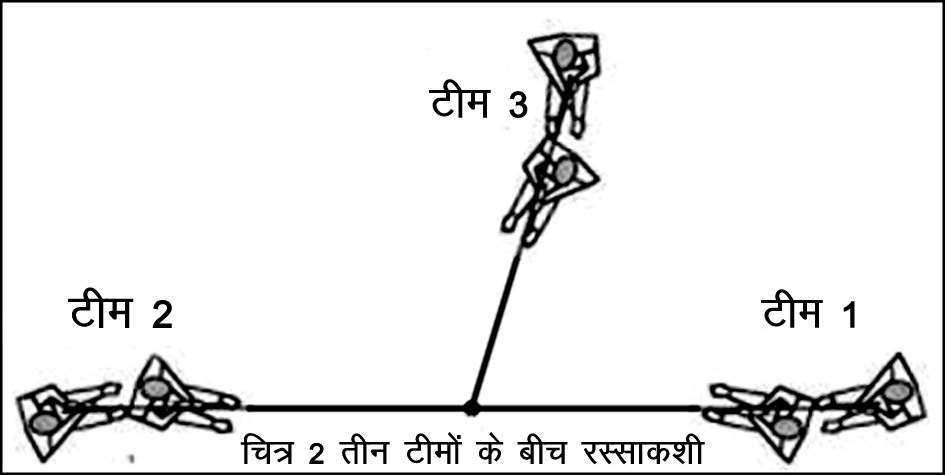 अब जिस प्रयोग की बात हम पहले कर रहे थे उस पर आते हैं। याद रहे कि यह प्रयोग हम तब ही कर पाएँगे जब दोनों बल बराबर हों यानी कि तंत्र सन्तुलित हो। बलों की इस सन्तुलित व्यवस्था में अब एक और बल जोड़ा जाए। रस्साकशी के खेल से तुलना करें तो ये ठीक वैसा ही होगा कि एक तीसरी टीम भी खेल के मैदान में उतर आए और चित्र-2 में दिखाए अनुसार बिन्दु ग्र् को अपनी तरफ खींचने की कोशिश करे। लेकिन कुछ शर्तें हैं जो इस नए बल पर लागू होंगी:
अब जिस प्रयोग की बात हम पहले कर रहे थे उस पर आते हैं। याद रहे कि यह प्रयोग हम तब ही कर पाएँगे जब दोनों बल बराबर हों यानी कि तंत्र सन्तुलित हो। बलों की इस सन्तुलित व्यवस्था में अब एक और बल जोड़ा जाए। रस्साकशी के खेल से तुलना करें तो ये ठीक वैसा ही होगा कि एक तीसरी टीम भी खेल के मैदान में उतर आए और चित्र-2 में दिखाए अनुसार बिन्दु ग्र् को अपनी तरफ खींचने की कोशिश करे। लेकिन कुछ शर्तें हैं जो इस नए बल पर लागू होंगी:
1. यह बल भी उसी तल (टेबल के सपाट पटिए) पर हो जिसमें पहले दोनों बल हैं। यानी कि सारे बल एक ही तल में (COPLANAR) हों;
2. इस बल का मान पहले दोनों बलों के बराबर हो, यानी कि F1=F2=F3और,
3. इसके लगने की दिशा पहले दोनों बलों की दिशा, यानी कि पूर्व या पश्चिम, ना हो।
अब सवाल यह उठता है कि इस नए बल को जोड़ने के बाद हमारे बलों के इस नए तंत्र का क्या होगा? बचपन में एक कहावत सुनी थी ‘तीन तिगाड़ा, काम बिगाड़ा’। तो क्या इस नए बल के चलते हमारी व्यवस्था बिगड़ जाएगी, क्या यह असन्तुलित हो जाएगी? या यह नई व्यवस्था सन्तुलन में होगी? अगर सन्तुलित होगी तो ऐसा किन परिस्थितियों में होगा? रस्साकशी के खेल के सन्दर्भ में हम यह सवाल पूछ सकते हैं कि जब सभी टीम समान बल लगा रही हों तो किस स्थिति में कोई टीम जीत सकती है।
क्या आपके पास जवाब हैं इन सवालों के? चाहें तो कुछ जुगाड़ लगाकर अपने लिए एक प्रयोग भी तैयार कर सकते हैं, जिससे आप इन सवालों की पड़ताल कर सकें। और अगर जुगाड़ न लगा पाएँ तो कागज़-कलम लेकर ही जुट जाइए।
सबसे पहले उन दो बातों पर गौर करें जो शायद हमारी मदद कर सकें, इन सवालों के जवाब खोजने में।
1. ये बात तो पक्की है कि बिन्दु O अब अपनी पहली वाली जगह पर नहीं रहेगा। ये हम कैसे कह सकते हैं? चित्र-1 में दिखाई गई परिस्थिति में दो बल आपस में सन्तुलन की स्थिति में हैं। एक तरीके से कह सकते हैं बिन्दु O पर लगने वाले बल F1व F2 एक-दूसरे के असर को काट रहे हैं। इसीलिए बिन्दु O तटस्थ है। ऐसे में अगर एक और बल इस व्यवस्था में जोड़ा जाए तो यह नई व्यवस्था तब तक सन्तुलन में नहीं रहेगी जब तक बिन्दु O पर लगने वाले सभी बल एक-दूसरे के असर को नहीं काट देते। चित्र-3 में दिखलाई गई स्थिति में F1 व F2 तो एक-दूसरे के असर को काट रहे हैं, लेकिन F3 के असर को काटने वाला कोई बल नहीं है।
हमारे इस अवलोकन से जो सवाल उभरकर आते हैं वे ये कि क्या एक बिन्दु पर लगने वाले समान मान के तीन बल एक-दूसरे के असर को काट सकते हैं? अगर हाँ, तो किस परिस्थिति में? ये सवाल ऊपर पूछे गए सवालों का एक और रूप ही है। इस पर आगे बढ़ने से पहले एक अन्य बात पर भी गौर कर लें।
2. हमने देखा कि दो बलों की सन्तुलित व्यवस्था में लाए गए इस तीसरे बल पर कुछ शर्तें लागू होती हैं। अगर आप इन शर्तों पर गौर करें तो पाएँगे कि पहली दो तो एकदम पक्की हैं। उनमें फेर-बदल की गुंजाइश नहीं। लेकिन जो आखिरी शर्त है वह लचीली है। उसे पूरा करने के लिए बस इतना ही काफी होगा कि नया बल पहले दो बलों की दिशा में न हो। यानी कि पूर्व या पश्चिम दिशा में न लग रहा हो। अब अगर इन दिशाओं को छोड़ दें तब भी हमारे पास अनगिनत दिशाएँ हैं, जिस तरफ से नया बल लगाया जा सकता है (देखें चित्र-4)। इसके अलावा एक और राशि भी है जिसका चुनाव हमारे हाथों में है - यह बल उस दिशा में कितनी दूरी से लगाया जाए। यानी कि T3 की स्थिति भी हम चुन सकते हैं। तो क्या, पहले बिन्दु में उठाए गए सवालों के जवाब इन दो राशियों के चुनाव से जुड़े हुए हैं?
जिन दो बातों पर हमने हाल ही में गौर किया वे हमारे सामने दो सवाल प्रस्तुत करती हैं:
1. किन परिस्थितियों में एक ही बिन्दु व एक ही तल (Plane) पर लग रहे तीन समान मान के बलों की व्यवस्था सन्तुलित होगी? व
2. बल लगाने की दिशा व स्थान के चुनाव का खेल के नतीजे पर क्या असर पड़ता है?
इन दोनों पर हम बारी-बारी से चर्चा करते हैं।
कब होगा सन्तुलन?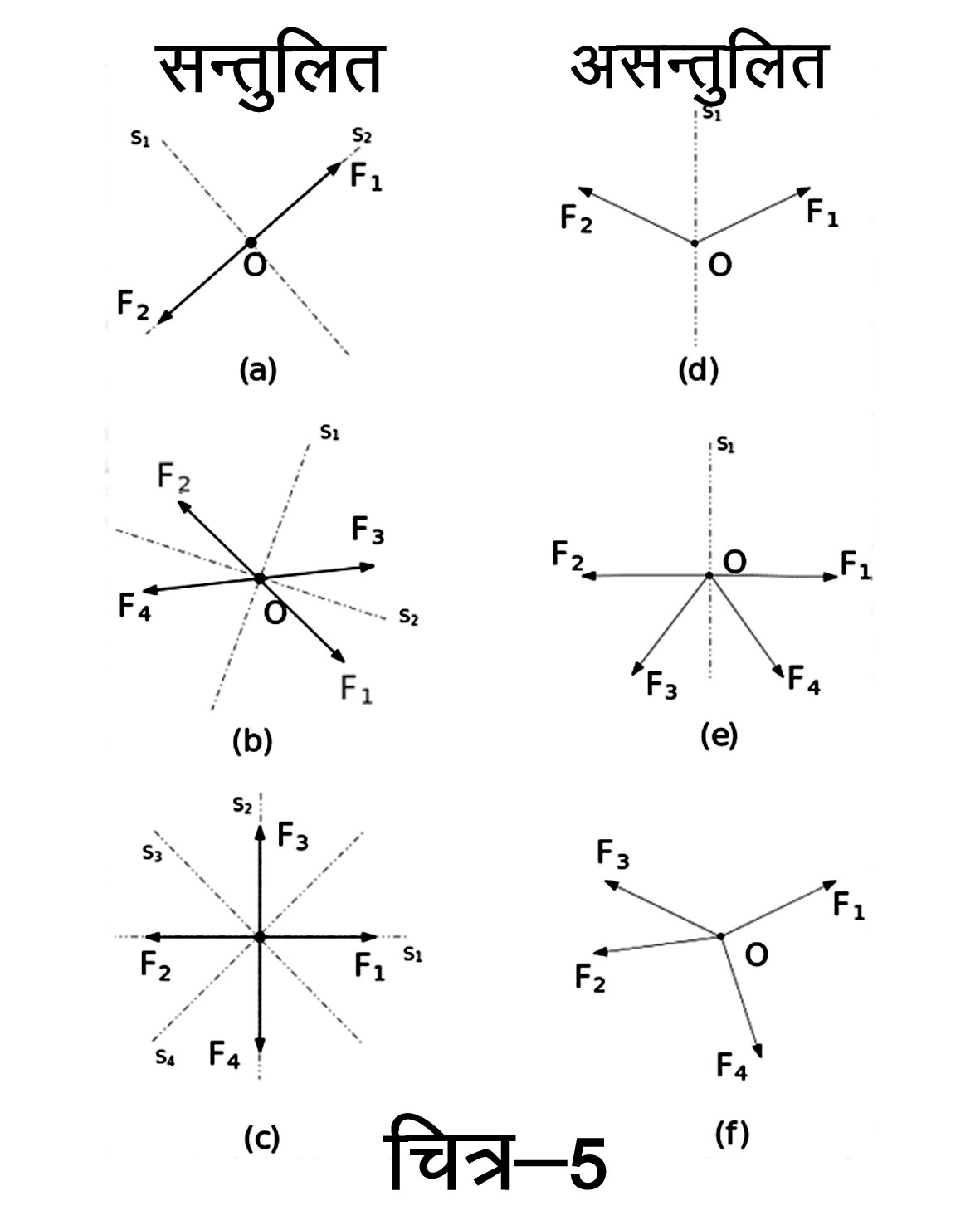 ध्यान रहे यहाँ चर्चा बलों की ऐसी व्यवस्था पर हो रही है, जिसमें सभी बल समान तल में हैं, एक ही बिन्दु पर लग रहे हैं व उन सभी का मान भी समान है। ऐसी व्यवस्था की समझ बनाने के कई तरीके हो सकते हैं।
ध्यान रहे यहाँ चर्चा बलों की ऐसी व्यवस्था पर हो रही है, जिसमें सभी बल समान तल में हैं, एक ही बिन्दु पर लग रहे हैं व उन सभी का मान भी समान है। ऐसी व्यवस्था की समझ बनाने के कई तरीके हो सकते हैं।
चित्र-5 में हमने कुछ बलों की व्यवस्थाएँ (system of forces) दिखाई हैं। चूँकि सभी बलों के मान समान हैं, इसीलिए बलों को दर्शाती रेखाओं की लम्बाई भी समान दिखाई गई है। चित्र-5 में बाईं ओर के दो व चार बलों वाली व्यवस्थाएँ सन्तुलन में हैं, व दाहिनी ओर की व्यवस्थाएँ असन्तुलित हैं। क्या आप इन चित्रों को देखकर बता सकते हैं कि ऐसा क्या है जो किसी व्यवस्था को सन्तुलित व दूसरी को असन्तुलित बनाता है, और हम उसकी पहचान कैसे कर सकते हैं?
एक तरीका है कि हम यह देखें कि किस व्यवस्था में हर एक बल की ठीक विपरीत दिशा में भी एक बल लग रहा है। ऐसा हुआ तो बलों की व्यवस्था सन्तुलित होगी, जैसे कि चित्र-5a, 5b व 5c में दिखाई गई व्यवस्थाएँ। और अगर ऐसा नहीं हुआ तो व्यवस्था असन्तुलित होगी, जैसे कि चित्र-5d, 5e व 5f में दिखाई गई व्यवस्थाएँ।
लेकिन क्या यह तरीका तीन बलों की व्यवस्था की पड़ताल करने के लिए इस्तेमाल किया जा सकता है? ज़ाहिर तौर पर तीन समान मान के बलों को चाहे जैसे भी जमाने की कोशिश करें, हम ऐसी व्यवस्था नहीं बना सकते जिसमें हर एक बल की ठीक विपरीत दिशा में भी एक बल लग रहा हो। तो यह तरीका सिर्फ ऐसी ही व्यवस्था की पड़ताल करने में काम आ सकता है जिसमें बलों की संख्या 2 से विभाजित की जा सके, यानी कि सम संख्या हो।
अब हमें कोई ऐसा तरीका खोजना होगा जो बलों की किसी भी संख्या वाली व्यवस्था के लिए इस्तेमाल किया जा सके।
अगर आप गौर करें तो देखेंगे कि चित्र-5 में जो व्यवस्थाएँ सन्तुलित हैं, उनमें कम-से-कम दो ऐसे अक्ष या लाइनें हैं जो उस व्यवस्था को दो समरूप भागों में बाँटतीं हैं। यानी कि इन अक्षों के दाईं व बाईं ओर के बलों की व्यवस्था एक-सी ही है। ऐसी किसी भी लाइन को हम सममिति की रेखा (line of symmetry) कहेंगे। चित्र 5a व 5b की व्यवस्थाओं में ऐसे दो अक्ष हैं s1 और s2। वहीं 5c की व्यवस्था में ऐसे चार अक्ष हैं। दूसरी ओर, असन्तुलित व्यवस्थाओं में या तो ऐसा एक ही अक्ष है (चित्र-5d व 5e) या एक भी नहीं (चित्र-5f)।
अब सवाल उठता है कि क्या हम तीन बलों की व्यवस्था को ऐसे बना सकते हैं कि उसमें कम-से-कम दो सममिति की रेखाएँ हों? और क्या यह तरीका हो सकता है जाँचने का कि तीन या ऐसी ही किसी विषम संख्या वाली बराबर मान के बलों की व्यवस्था सन्तुलित है या नहीं?
सबसे पहले तो हम तीन बलों को ऐसे रखने की कोशिश करते हैं कि उसमें कम-से-कम दो सममिति की रेखाएँ हों। अगर आप ऐसा कर पाएँ तो आपको चित्र-6 में दिखाई गई व्यवस्था मिलेगी, जिसमें हर एक बल अपने बगल वाले बल से 1200 के कोण पर है जिसके चलते इस व्यवस्था में दो नहीं बल्कि तीन सममिति की रेखाएँ हैं। और यह व्यवस्था सन्तुलित होगी। आइए देखते हैं क्यों। लेकिन उससे पहले ज़रा यह देख लें कि संख्या ‘दो’ में क्या खास बात है।
‘दो’ में ऐसा क्या है खास?
अगर हमें किसी कागज़ पर एक खास बिन्दु की स्थिति बतानी हो तो हम कैसे बताएँगे? हम कह सकते हैं कि निचले छोर से वह बिन्दु फलाँ दूरी पर है। पर क्या इतना बताना ही काफी होगा? नहीं! क्योंकि निचले छोर से उस दूरी पर अनगिनत बिन्दु होंगे। अगर हम निचले छोर के साथ-साथ ऊपरी छोर से भी बिन्दु की दूरी बतलाएँ तब क्या हम बिन्दु की स्थिति को सही-सही बतला सकते हैं? इसका जवाब भी नकारात्मक होगा। सोचिए क्यों।
असल में एक कागज़ पर किसी भी बिन्दु की स्पष्ट स्थिति बतलाने के लिए हमें दो ऐसे किनारों को लेना होगा जो एक ही दिशा को न दर्शाते हों, वे समानान्तर न हों (देखें चित्र-7)। जैसे कि निचला व बायाँ, या निचला व दायाँ, या ऊपरी व दायाँ, या कि ऊपरी व बायाँ। इनमें से किसी भी एक जोड़े का इस्तेमाल कर हम एक कागज़ पर किसी भी बिन्दु की स्थिति स्पष्ट तरीके से बता सकते हैं। अगर हमें किसी बिन्दु की स्थिति तीन किनारों से पता हो तो हमारे पास ज़रूरत से ज़्यादा जानकारी होगी।
एक कागज़ या समतल (जैसे कि टेबल) पर किसी बिन्दु को स्पष्ट तौर से दर्शाने के लिए हमें दो स्वतंत्र दिशाओं की ज़रूरत पड़ती है। इसीलिए एक ग्राफ बनाते समय भी हम सबसे पहले दो स्वतंत्र अक्षों को दर्शाते हैं। आसानी के लिए हम इनके बीच का कोण 900 का ले लेते हैं।
ऐसे ही एक बल को हमने चित्र-8 के ग्राफ में दर्शाया है। बल जिस बिन्दु पर लग रहा है उसे ही हमने सन्दर्भ-बिन्दु मान लिया है। चूॅँकि बल एक सदिश राशि है तो हमें ग्राफ पर इसकी लम्बाई, जो इसके मान को दर्शाएगी, के साथ-साथ यह भी दिखाना होगा कि बल किस दिशा में लग रहा है1।
सदिश राशियों से जुड़े गणितीय नियमों से हम जानते हैं कि हम इन राशियों को चित्र-8 में दिखाए अनुसार x-अक्ष व y-अक्ष के भागों में बाँटकर देख सकते हैं। इस तरह अगर आप चित्र-6 में दिखाई गई व्यवस्था के बलों को उनके x-अक्ष व y-अक्ष के भागों में बाँटकर देखेंगे तो पाएँगे कि इन दोनों अक्षों की दिशाओं में लगने वाले बल एक-दूसरे को काट रहे हैं, जिस वजह से यह व्यवस्था सन्तुलन में है।
चित्र-9 में इस व्यवस्था को एक अलग तरह से दर्शाया गया है। इस व्यवस्था के सभी बलों को उनके x-अक्ष व y-अक्ष के भागों में बाँटकर तालिका-1 में दिखलाया गया है। तालिका में आप देख सकते हैं कि बिन्दु o पर लगने वाला कुल बल शून्य के बराबर है, जिस वजह से यह एक सन्तुलित बल व्यवस्था है।
हमने सममिति की रेखाओं वाले जिस तरीके का ज़िक्र पहले किया वो सिर्फ उन व्यवस्थाओं पर ही लागू किया जा सकता है जिनमें सभी बल समान मान के हों। बलों को उनके भागों में बाँटकर देखने के तरीके से आप किसी भी तरह की बल-व्यवस्था के सन्तुलन में होने या न होने का पता लगा सकते हैं। 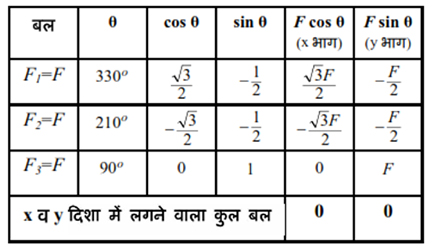 क्या हो पाएगा सन्तुलन?
क्या हो पाएगा सन्तुलन?
यह साफ हो जाने के बाद कि एक ही तल व बिन्दु पर लग रहे तीन बराबर मान के बलों के लिए सन्तुलन की स्थिति क्या होगी, आइए अब रस्साकशी के खेल पर वापिस चलते हैं। चित्र-3 के सन्दर्भ में हमने देखा कि तीसरे बल के लगने के साथ दो बलों की सन्तुलित व्यवस्था असन्तुलित हो जाएगी। पर सवाल यह उठता है कि क्या यह नई व्यवस्था सन्तुलन में आ पाएगी? आप शायद सोच रहे हों अब जबकि हमें पता है कि तीन बलों की व्यवस्था किस स्थिति में सन्तुलित होती है, यह सवाल उठाने का क्या मतलब। सीधी-सी बात लगती है कि जैसे ही हम तीसरा बल दो बलों की सन्तुलित व्यवस्था में जोड़ेंगे तो बिन्दु ग्र् अपनी पुरानी जगह से हटकर उस स्थिति में जाने की कोशिश करेगा जिसमें यह नई व्यवस्था सन्तुलित हो यानी कि चित्र-6 वाली स्थिति। लेकिन क्या यह हमेशा हो पाएगा? अगर ऐसा हो पाता तो इस लेख को हम आगे न बढ़ाते। मज़ेदार बात यही है कि ऐसा हमेशा सम्भव नहीं होगा, क्योंकि नई व्यवस्था का सन्तुलित या असन्तुलित होना इस बात पर निर्भर करता है कि तीनों बलों की पारस्परिक स्थिति कैसी है। आइए समझने की कोशिश करते हैं।
|
बॉक्स -1
α1 + α1 + α1 = 180o (1) व त्रिभुज T1 O T2 के लिए: s1 + s2 + β3 = 180o (2) समीकरण (1) व (2) को मिलाकर देखें तो हम कह सकते हैं कि: α1 + α2 + α3 = s1 + s2 + β3 (3) इसी तरह दूसरे तथ्य से हमें पता चलता है कि: α1 > s1 (4) और α2 > s2 (5) समीकरण (4) व (5) को मिलाकर देखें तो हम कह सकते हैं कि: α1 + α2 > s1 + s2 (6) समीकरण (3) व (6) की तुलना करने पर हम साफ-साफ देख सकते हैं कि β3 > α3 होगा |
चित्र-10 में दिखाए अनुसार तीनों टीमों की स्थिति एक त्रिभुज बनाती है जिसमें α1 , α2 व α3 क्रमश: T1 , T2 व T3 कोनों पर बनने वाले आन्तरिक कोण हैं। अब अगर इस त्रिभुज के अन्दर हम एक बिन्दु O लें व उसे त्रिभुज के कोनों से जोड़कर कोण β1, β2 व β3 बनाएँ तो हम देख सकते हैं कि त्रिभुज के अन्दर O की किसी भी स्थिति के लिए β1 > α1 , β2 > α2 व β3 > α3 होगा। त्रिभुज T1 T3 T2 व T1 O T2 की तुलना कर इस तथ्य को आसानी से देख सकते हैं कि β3 > α3 होगा। इसी तरह त्रिभुज T1 T2 T3 की क्रमशः T1 O T3 व T2 O T3 से तुलना करके देखा जा सकता है कि β2 > α2 व β1 > α1 होगा। करके देखिए या देखिए बॉक्स-1।
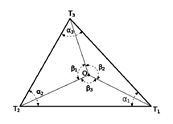 आप यह भी देखेंगे कि जैसे-जैसे बिन्दु O की एक कोने से दूरी बढ़ती जाती है, उस कोने से सम्बन्धित कोण भी बड़ा होता जाता है। उदाहरण के तौर पर, अगर बिन्दु O, T3 से दूर जाए तो β3 का मान बढ़ेगा। इसका मतलब हुआ कि β3 सबसे छोटा तब होगा जब बिन्दु O व T3 एक ही जगह पर हों व सबसे बड़ा तब जब बिन्दु Ο लाइन T2T1 पर हो। इस तरह हम कह सकते हैं 180o ≥ β3 ≥ α3। इसका मतलब हुआ कि अगर α3 का मान 120o से ज़्यादा हुआ तो कोण β3 > 120o होगा। β1 व β2 के लिए भी यही बात लागू होगी।
आप यह भी देखेंगे कि जैसे-जैसे बिन्दु O की एक कोने से दूरी बढ़ती जाती है, उस कोने से सम्बन्धित कोण भी बड़ा होता जाता है। उदाहरण के तौर पर, अगर बिन्दु O, T3 से दूर जाए तो β3 का मान बढ़ेगा। इसका मतलब हुआ कि β3 सबसे छोटा तब होगा जब बिन्दु O व T3 एक ही जगह पर हों व सबसे बड़ा तब जब बिन्दु Ο लाइन T2T1 पर हो। इस तरह हम कह सकते हैं 180o ≥ β3 ≥ α3। इसका मतलब हुआ कि अगर α3 का मान 120o से ज़्यादा हुआ तो कोण β3 > 120o होगा। β1 व β2 के लिए भी यही बात लागू होगी।
इन कोणों व इनके बीच के सम्बन्धों पर इतनी बातचीत के बाद ये बातें साफ हो जाती हैं कि,
* अगर तीनों बलों की पारस्परिक स्थिति ऐसी है कि तीनों में से कोई भी आन्तरिक कोण 120o से बड़ा न हो तो पक्के तौर से त्रिभुज के अन्दर एक ऐसा बिन्दु होगा जिस पर चित्र-6 में दिखलाई गई सन्तुलन की स्थिति बनेगी। इस स्थिति में बिन्दु O इस बिन्दु पर जाकर रुक जाएगा व तीन बराबर बलों की व्यवस्था सन्तुलन में होगी। रस्साकशी के खेल के सन्दर्भ में देखें तो कोई भी टीम नहीं जीतेगी।
* दूसरी तरफ, अगर कोई भी आन्तरिक कोण 120o के बराबर या उससे ज़्यादा हुआ तो त्रिभुज के अन्दर ऐसा कोई भी बिन्दु नहीं होगा। ऐसी स्थिति में बिन्दु ग्र् उस कोने की तरफ जाएगा जिस पर आन्तरिक कोण 120o के बराबर या उससे ज़्यादा हो। जिसका मतलब रस्साकशी के खेल के सन्दर्भ में यह हुआ कि वो टीम जीतेगी जिसके कोने पर बनने वाला आन्तरिक कोण 120o के बराबर या उससे ज़्यादा हो।
कुल मिलाकर इस लेख में हमने देखा कि एक बिन्दु पर लग रहे तीन समतल व बराबर बलों की एक व्यवस्था का सन्तुलन में होना या न होना बलों की आपसी स्थिति पर निर्भर करता है।
तो अगर आप रस्साकशी के एक ऐसे खेल में पड़ गए हों जिसमें टीमें तीन हों एवं वे बराबर मान का बल लगा रही हों और आप स्वतंत्र हों अपनी टीम का स्थान चुनने के लिए तो अब आपको पता है कि जीतने के लिए आपको क्या करना होगा!
विवेक मेहता: आई.आई.टी., कानपुर से मेकेनिकल इंजीनियरिंग में पीएच.डी. की है। एकलव्य के विज्ञान शिक्षण कार्यक्रम के साथ फैलोशिप पर हैं।




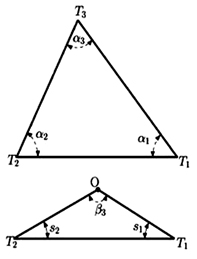 वैसे तो रेखाचित्र देखकर ही स्पष्ट हो जाता है कि β3>α3 परन्तु यहाँ हम ज्यामितीय आकृतियों एवं समीकरणों की मदद से इसे प्रमाणित करने का प्रयास कर रहे हैं।
वैसे तो रेखाचित्र देखकर ही स्पष्ट हो जाता है कि β3>α3 परन्तु यहाँ हम ज्यामितीय आकृतियों एवं समीकरणों की मदद से इसे प्रमाणित करने का प्रयास कर रहे हैं।