अमिताभ मुखर्जी
दबाव की अवधारणा अक्सर उलझन में डाल देती है। ठोस, द्रव और गैस के निहित गुणधर्मों में फर्क की वजह से किसी बर्तन पर कितना और कहां दबाव महसूस होता है? कैसे पता चलता है कि कहां दबाव ज्यादा है और कहां कम? दो खंड में बंटे इस लेख में ऐसी बहुत-सी बातों को समझने की कोशिश करेंगे।
बाव शब्द का उपयोग आम ज़िन्दगी में कई तरह से किया जाता है। जैसे कोई भारी वस्तु उठाने में हाथों पर दबाव महसूस होता है। चढ़ाई पर साइकिल चलाते समय पैरों में अधिक दबाव लगता है। परीक्षा से पहले छात्र मानसिक दबाव में होते हैं। जब हम हवा के दबाव की बात करते हैं, तो दबाव का विशेष अर्थ क्या होता है इसे समझने के लिए आइए एक छोटा-सा प्रयोग करते हैं।
इस प्रयोग के लिए हमें एक ईंट या ईंट के आकार का लकड़ी का गुटका या कांच की स्लैब चाहिए। साथ ही जरूरत है कुछ रेत या आटे की। रेत को एक परात, गमले या चिलमची में रख लें।
पहले रेत या आटे का एक ढेर बनाइए और उसकी सतह को हाथ से बराबर कर लीजिए। इस स्थिति में उसकी ऊंचाई कम-से-कम 5 से.मी. होनी चाहिए।
अब उस पर चित्र-1(क) की तरह ईंट को रखिए। ध्यान रहे कि ईंट को घसीटना नहीं है, न ही उसे ऊपर से छोड़ना है। बस धीरे से रेत के ऊपर बिठाना है।
अब ईंट को धीरे से हटा लीजिए। ईंट के भार से बने हुए गड्ढे को देखिए। (अगर ईंट हटाते ही गड्ढा भर जाता है तो ईंट रखने की क्रिया को फिर से करना होगा।) गड्ढे की गहराई कितनी है? अब ईंट को चित्र-1(ख) और (ग) की तरह रख कर प्रयोग को दोहराइए। हर बार ईंट रखने से पहले रेत की सतह को हाथ से बराबर करना होगा, ताकि तीनों बार ईंट रखते समय रेत की स्थिति एक जैसी हो। क्या तीनों बार बने हुए गड्ढों की गहराई बराबर है?
यह तो ज़ाहिर है कि ईंट के भार से रेत दब जाती है। ईंट का भार तो तीनों स्थितियों में बराबर है। पर भार का असर पड़ता है ईंट के आधार या नीचे वाले पहलू पर। चित्र-1 (क) में आधार सबसे बड़ा है - यानी उसका क्षेत्रफल सबसे अधिक है और चित्र - 1 (ग) में सबसे छोटा है यानी उसका क्षेत्रफल सबसे कम है।
ऊपर दिए गए प्रयोग और तर्क से ‘दबाव' की एक परिभाषा उभरती हैः
दबाव = बल / क्षेत्रफल
चित्र-1(क), (ख) और (ग) में बल एक समान है, ईंट का भार ही वह बल है। पर क्षेत्रफल अलग -अलग हैं। चित्र-1 (क) में बल सबसे अधिक क्षेत्रफल वाली सतह पर लग रहा है। अतः दबाव सबसे कम है। चित्र-1(ख) में क्षेत्रफल कम है, अतः दबाव अधिक है। चित्र-1 (ग) में बल सबसे कम क्षेत्रफले पर लग रहा है, इसलिए दबाव सबसे अधिक है।
द्रव का दबाव
ईंट और दूसरी ठोस वस्तुओं की तरह पानी और अन्य द्रव भी अपने भार के कारण आधार पर दबाव डालते हैं।
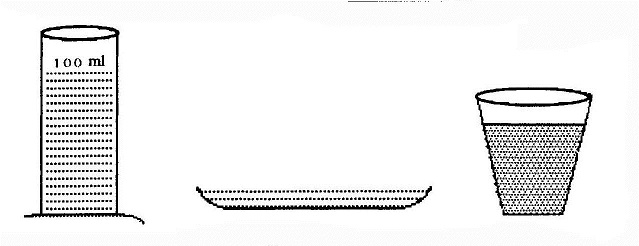
पर ठोस वस्तुओं में और द्रवों में एक बहुत बड़ा अंतर है। द्रवों की अपनी कोई आकृति नहीं होती, उन्हें जिस बर्तन में रखा जाता है वे उसी की आकृति धारण करते हैं। केवल उनका आयतन नहीं बदलती; जैसे चित्र-2 में सौ मिली लीटर पानी अलग-अलग पात्रों में रखा है।
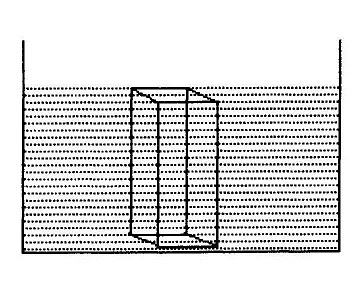मान लीजिए कि चित्र-2 जैसे नपनाघट या उसी आकार के बर्तन में 10 से.मी. की ऊंचाई तक पानी भरा है। हम पानी से बनी एक ईंट' की कल्पना कर सकते हैं, जिसकी ऊंचाई 10 से. मी., लंबाई 1 से. मी. और चौड़ाई 1 से. मी. है। (चित्र-3)
इस ईंट का आयतन 10 x 1 x 1 = 10 घन से.मी. है। चूंकि एक घन से. मी. पानी का भार एक ग्राम होता है इस पानी से बनी ईंट का भार दस ग्राम है। यह भार ईंट के आधार पर काम कर रहा है। आधार का क्षेत्रफल 1 से.मी. x 1 से.मी. = 1 वर्ग से.मी. है। लेख के शुरुआत में दबाव के सूत्र की चर्चा की थी, उसके अनुसार इस पानी की ईंट की वजह से बर्तन के आधार पर लग रहे दबाव की गणना कर सकते हैं।
दबाव = बल / क्षेत्रफल
= 10 ग्राम/1 वर्ग से.मी.
= 10 ग्राम/वर्ग से.मी.
इसको इस तरह भी लिख सकते हैं:
पानी का दबाव = 10 से.मी. x 1 ग्राम/घन से.मी.
= ऊंचाई x 1 घन से.मी. पानी को भार
अगर पानी की जगह कोई दूसरा द्रव होता तो क्या होता? अन्य सब मात्राएं यानी ऊंचाई और आधार का क्षेत्रफल तो वही रहेंगे; पर 1 घन से.मी. का भार हर द्रव के लिए 1 ग्राम नहीं होता। 1 घन से. मी. के भार को द्रव का घनत्व कहते हैं।
तो फिर किसी अन्य द्रव से बनी ईंट का दबाव क्या होगा?
द्रव का दबाव (ग्राम/वर्ग से.मी.) = ऊंचाई (से.मी.)xघनत्व (ग्राम/घन से.मी.)
यह एक महत्वपूर्ण सूत्र है। यही हमें बताता है कि द्रव से भरे किसी बर्तन के आधार पर कितना दबाव होगा, या तालाब, नदी या समुद्र में गोता लगाने वाला व्यक्ति कितनी गहराई पर कितना दबाव महसूस करेगा।
अब आप पूछेंगे कि एक ठोस ईंट या धातु या लकड़ी के गुटके में और द्रव से बनी काल्पनिक ईंट में क्या कोई अंतर नहीं है? क्योंकि गुटके के आधार पर भी उसके भार के कारण दबाव पड़ता है। हां, इनमें बहुत बड़ा अंतर है। जैसा कि हमने पहले ही कहा है, द्रव को जिस बर्तन में रखेंगे वह उसी की आकृति धारण करेगा। उसकी प्रवृति फैलने या बहने की है। जहां भी द्रव और बर्तन संपर्क में हैं, द्रव फैलने की कोशिश करता है, जिससे बर्तन पर जोर लगता है। अतः द्रव का दबाव केवल आधार पर नहीं, बल्कि बर्तन की दीवारों पर पड़ता है। चित्र 4 में कुछ पात्र दिखाए गए हैं जिनमें पानी भरा है।
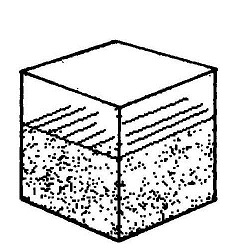
इन सभी में ‘क’ बिन्दु पर दबाव बराबर है। क्योंकि ये बिन्दु समान गहराई पर हैं। यानी ‘क’ से ऊपरी सतह तक पानी की ऊंचाई बराबर है, और दबाव केवल इस ऊंचाई पर निर्भर है, बर्तन की आकृति पर नहीं। द्रव और ठोस वस्तु में अंतर देखिए। चित्र 5 में एक प्लास्टिक के डिब्बे में लकड़ी का गुटका रखा है। गुटका डिब्बे की दीवारों को छू रहा है, पर चूंकि उसकी अपनी आकृति तय है, वह दीवारों पर कोई दबाव नहीं डालता। केवल आधार पर दबाव डालता है।
द्रवों के दबाव न झेल पाने के इस गुणधर्म को ‘तरलता' (fluidity) कहते हैं। अगर उन्हें कहीं रास्ता मिलता है, तो वे दबाव से दूर भागते हैं, अर्थात बहने लगते हैं। एक लंबी ऊंची नली में अगर पानी भरा हो, तो उसके निचले भाग पर दबाव पड़ता है। ऐसे में अगर निकलने का रास्ता मिले तो पानी जोरों से बहने लगता है (चित्र 6)। यही है घरों में लगी पानी की टोटी का राज़।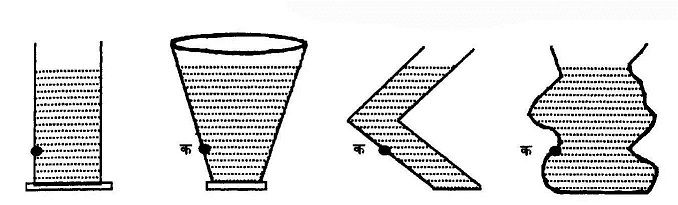 
अगर द्रव को किसी बंद बर्तन में रखकर उसे एक तरफ से दबाया जाए तो? तो द्रव के ज़रिए यह दबाव उसके हर भाग में समान रूप में पहुंच जाता है। फ्रांसीसी वैज्ञानिक पास्कल ने सबसे पहले द्रवों के इस सामान्य गुणधर्म को समझा था, इसलिए इसे पास्कल का नियम कहते हैं।
हवा में बातें?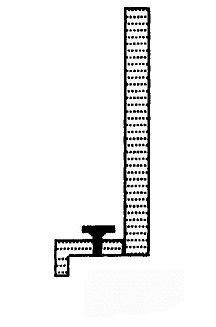 
अब शायद आप कहेंगे, “यह तो हवा में बातें हो रही हैं। हवा की बात तो शुरू ही नहीं हुई। इस सब से हवा के दबाव का क्या संबंध?"
हवा और अन्य गैसें एक दृष्टि से द्रवों की तरह हैं - इनमें भी तरलता या बहने की प्रवृत्ति होती है। पर द्रवों और गैसों में एक अंतर भी है। द्रव पात्र के साथ-साथ अपनी आकृति भी बदल लेते हैं, पर उनका आयतन नहीं बदलता। अगर पानी से भरे गुब्बारे को दबाने की कोशिश करें, तो क्या होता है? पास्कल के नियम के अनुसार दबाव पूरे गुब्बारे पर एक समान लगता है। हमने गुब्बारे को किस तरह पकड़ा है, उस पर निर्भर है उसकी आकृति।
गोताखोरः कांच के जार में पानी भरकर उसमें गोताखोर को छोड़ना है। उसके बाद जार के मुंह को रबर के टुकड़े से बंद कर देते हैं। अब स्थिति 7-क जैसी हो गई यानी गोताखोर अभी तैर रहा है। अब रबर के टुकड़े को दबाते हैं। रबर दबाने पर गोताखोर पानी में नीचे चला जाता है यानी चित्रः 7-ख की तरह जैसे ही रबर के टुकड़े पर से दबाव हटाते हैं वैसे ही फिर से गोताखोर ऊपर आ जाता है। गोताखोर के इस ऊपर-नीचे जाने का राज़ जानना हो तो चित्रः 7-ग देखिए। गोताखोर का पेट पोला है, एक नलीनुमा रचना जो एक तरफ से बंद है। जरा सोचिए इस हवा भरी नली की गोताखोर के ऊपर-नीचे होने से भला क्या संबंध होगा?
पर एक जगह से अगर गुब्बारा पिचक जाए तो दूसरी जगह से बाहर निकल आता है। यानी दबाव से पानी की आकृति जरूर बदली, पर आयतन नहीं बदला। यही प्रयोग अगर हवा से भरे गुब्बारे से करें, तो हम देखेंगे गुब्बारे को चारों ओर से दबाने पर वह छोटा हो जाता है। यानी हवा या कोई भी गैस दबाने पर संकुचित हो जाती है। उसका आयतन निश्चित नहीं होता।
हवा के इस गुणधर्म पर आधारित है एक मजेदार खिलौना। (चित्र-7)
एक चौड़े मुंह वाले कांच के बर्तन में लगभग आधा पानी भरा होता है। बर्तन का मुंह पहले रबड़ से ढका होता है, जैसे किसी बड़े गुब्बारे या साइकिल की ट्यूब के टुकड़े से। पानी में पुतला तैर रहा होता है (चित्र 7 क)। ऊपर के रबड़ को हाथ से धीरे से दबाने पर पुतला नीचे गोता लगाता है (चित्र-7ख), हाथ हटा लेने पर पुतला फिर से ऊपर आ जाता है।
महान फ्रांसीसी दार्शनिक देकार्त (Descartes) के नाम से इस खिलौने को 'कार्लेसीय गोताखोर' कहते हैं।
क्या है इस गाताखार का राज़? वास्तव में पुतले में एक ऊपर से बंद नली होती है, जिसमें हवा भरी होती है। (चित्र-7 ग)
पुतले का भार इतना होता है कि वह इस हवा के सहारे तैर सके। ऊपर के रबड़ को हाथ से दबाने पर यह दबाव हवा के ज़रिए पानी पर पड़ता है, और पास्कल के नियम के अनुसार नली में भरी हवा पर भी पड़ता है। दबाव से हवा संकुचित हो जाती है (उसका आयतन कम हो जाता है) और नली में कुछ पानी घुस आता है। अगर पुतले का भार और नली का आयतन सही हो, तो इतना पानी पुतले को डुबाने के लिए काफी होता है; इसलिए वह गोता मारता है। दबाव हटा लेने पर हवा का आयतन फिर से पहले जितना हो जाता है। पानी बाहर निकल जाने पर पुतला हल्का हो जाता है और फिर से तैरने लगता है।
क्या आप इस विवरण के आधार पर यह खिलौना या इसी सिद्धांत पर आधारित कोई और खिलौना बना सकते हैं? काम थोड़ा नाजुक है, क्योंकि अगर पुतले का भार सही न हो, तो वह दोनों स्थितियों में तैरेगा या डुबेगा। कोशिश करके देखिए, और क्या होता है हमें लिख भेजिए।
अमिताभ मुखर्जी: दिल्ली विश्वविद्यालय में भौतिक शास्त्र पढ़ाते हैं।