नरेश दधीच
पूर्णता के लिहाज़ से शुरू से ही शुरू करते हैं। अर्थात शुरुआत क्लासिकी भौतिकी शास्त्र के न्यूटनीय खाके से करते हैं। हमारे सामने गति के तीन नियम हैं। इनमें से पहला नियम एक साम्य का कथन है कि एकरूप गति (यानी सरल रेखा में एकरूप चाल से गति और गतिहीनता समान हैं। इसका मतलब यह है कि आप कोई भी भौतिक प्रयोग करें, इन दो अवस्थाओं के बीच भेद करना असंभव है। यदि स्थिति इससे भिन्न है तो यह किसी बाहरी क्षेत्र अथवा बल की उपस्थिति की द्दोतक होगी। किसी बल-मुक्त क्षेत्र में कोई भी कण उपरोक्त में से किसी एक अवस्था में होगा। अवस्था कौन-सी होगी यह प्रारंभिक स्थितियों पर निर्भर करता है। यहां यह मानकर चला जाता है कि वह कण बाहर से प्रदत्त यानी दी गई एक इकाई है, और इस बात पर कोई ध्यान नहीं दिया जाता कि वह कण अस्तित्व में कैसे आया और उसकी रचना करने में कितनी ऊर्जा खर्च की गई है।
इस संदर्भ में एक मान्यता है जो लगभग आस्था के स्तर पर है कि भौतिक रूप से अनगण्य कोई भी बात ऊर्जा खर्च किए बगैर हो नहीं सकती और यदि किसी चीज़ का भौतिक अस्तिस्व है तो उसमें ऊर्जा अवश्य होगी। इसका अर्थ है कि न्यूटनीय भौतिकी में उपस्थित प्रत्येक कण में ऊर्जा होगी ही, चाहे वह कण विराम की स्थिति में ही क्यों न हो। इसे विराम ऊर्जा (स्थितिज ऊर्जा) कह सकते हैं। अर्थ को इतना विस्तार देने के बाद हम कह सकते हैं कि मुक्त आकाश में किसी कण की ऊर्जा उसकी गतिज ऊर्जा और विराम ऊर्जा के योग के बराबर होती है। जब कण विराम अवस्था में होता है तब उसकी सारी ऊर्जा विराम ऊर्जा यानी स्थितिज ऊर्जा के रूप में होती है।
तो उस कण के बारे में क्या कहेंगे जो कभी विराम अवस्था में होता ही नहीं, सदैव गति में रहता है। अर्थात उसकी सारी ऊर्जा गतिज ऊर्जा है, और उसकी विराम ऊर्जा शून्य है। इस कण का अस्तित्व ही इसकी गति में है।
ऐसा कण बाकी समस्त वस्तुओं के सापेक्ष गति करता रहेगा। इसे किसके सापेक्ष, और कितनी चाल से गति करना चाहिए? चूंकि यह कण सबके सापेक्ष गति कर रहा है, इसलिए सबके सापेक्ष इसे एक ही चाल से गति करना चाहिए। यदि प्रकृति में ऐसा कोई कण है तो एक ऐसी सार्वभौमिक (अपरिवर्तनशील) गति का भी अस्तित्व होगा जो सभी प्रेक्षकों के लिए सीमांत यानी चरम गति होगी।
राशनखयाल
प्रकाश एक ऐसी चीज़ है जो सदैव गतिशील रहती है और किसी के भी सापेक्ष स्थिर नहीं होती। प्रकाश एक विद्युत चुम्बकीय तरंग है जो विद्युतगतिकी संबंधी मैक्सवेल के सिद्धांतों के अनुसार गति करती है। किसी भी तरंग की चाल पूरी तरह उस माध्यम पर निर्भर करती है जिसमें से होकर बह गुज़र रही है। अर्थात इसकी चाल को तभी बदला जा सकता है जब या तो माध्यम को चलायमान किया जाए या बदल दिया जाए। यदि एक ऐसा माध्यम हो जो सर्वत्र व्याप्त हो, जिसे न चलायमान किया जा सके, न बदला जा सके, तो ऐसे माध्यम में प्रकाश की चाल सबके सापेक्ष एक
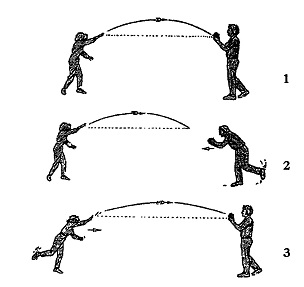गतियों को योगः दो खिलाड़ी गेंद के साथ खेल रहे हैं। यहां तीन स्थितियां दिखाई गई है। एक; दोनों खिलाड़ी अपनी-अपनी जगह पर खड़े हैं। एक खिलाड़ी दूसरे की ओर 10 मीटर/सेकेंड की रफ्तार से गेंद फेंक रहा है। दोः एक खिलाड़ी दूसरे की और 5 मीटर/सेकेंड की रफ्तार से दौड़ लगा रहा है और दूसरा खिलाड़ी पहले की ही तरह 10 मीटर/सेकेंड की रफ्तार से गेंद फेंक रहा है। यानी कैच पकड़ने वाले खिलाड़ी के लिए गेंद की गति 15 मीटर/सेकेंड हुई। यानी दोनों की गतियों का जोड़। तीनः गेंद फेंकने वाले खिलाड़ी ने 5मीटर/सेकेंड की रफ्तार से दौड़ते हुए गेंद 10 मीटर/सेकेंड की गति से फेंकी। इस बार भी कैच पकड़ने वाले खिलाड़ी के लिए गेंद की रफ्तार 15 मीटर/सेकेंड ही थी।
सार्वभौमिक स्थिरांक होगी। निर्वात ऐसा ही माध्यम है जिसमें प्रकाश गमन करता है। अतः इस माध्यम में प्रकाश की चाल अपरिवर्तनीय स्थिरांक होगी। प्रकाश का एक क्वांटम ही वह कण है जिसकी विराम ऊर्जा यानी स्थितिज ऊर्जा शून्य होती है और जो किसी भी प्रेक्षक यानी अवलोकनकर्ता के सापेक्ष विराम अवस्था में नहीं रह सकता।
यानी प्रकृति में एक ऐसी भौतिक चीज़ है जो अपरिवर्तनीय स्थिर चाल से गति करती है। यह चाल समस्त भौतिक कणों के लिए सीमांत (अधिकतम) चाल है। इस तथ्य का समावेश
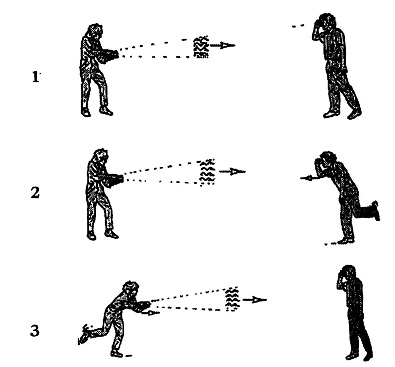गतियों का योग? गेंद वाले प्रयोग की ही तरह का एक प्रयोग प्रकाश के साथः
एकः दो व्यक्तियों में से एक के हाथ में टॉर्च है। पहली स्थिति में जब दोनों अपनी-अपनी जगह खड़े हैं। क्षण भर के लिए टॉर्च जलाने पर टॉर्च की रोशनी 30,00,00,000 मीटर/सेकेंड की रफ्तार से दूसरे व्यक्ति तक पहुंचती है। दोः जब पहला व्यक्ति टॉर्च जलाता है उस वक्त दूसरा 5 मीटर प्रति सेकेंड की रफ्तार से उसकी ओर दौड़ रहा है।
तीनः टॉर्च थामे हुए व्यक्ति 5 मीटर प्रति सेकेंड की गति से दौड़ रहा है और दौड़ते हुए वो टॉर्च जलाता है।
दूसरे और तीसरे, इन दोनों उदाहरणों में प्रकाश की किरण देखने वाले को प्रकाश 30,00,00,005 मीटर/सेकेंड की रफ्तार से आता हुआ नहीं दिखता जैसा कि पहले उदाहरण में हमने देखा था, बल्कि उसकी रफ्तार 30,00,00,00 मीटर प्रति सेकेंड ही रहती है।
ऐसा इसलिए होता है क्योंकि दरअसल दो जड़त्वीय फ्रेम के वेग के जोड़ का नियम । v=(V, +v,1+V,v/e) है। अगर दोनों की गति प्रकाश की गति की तुलना में काफी कम है तो समीकरण का नीचे वाला हिस्सा लगभग एक हो जाता है जिसके कारण हमारे आसपास की सामान्य घटनाओं में V= (v + v,) समीकरण अभी भी उतनी ही कारगरता के साथ काम करता है।
इन उदाहरणों में हमने माध्यम के रूप में हवा की मौजूदगी एवं प्रकाश किरणों के पास पृवी की उपस्थिति की वजह से प्रकाश की गति में होने वाले नगण्य परिबर्तनों को नज़रअंदाज़ किया है।
करने के लिए ज़रूरी हो जाएगा कि न्यूटनीय यांत्रिकी में आमूल संशोधन किए जाएं। इस संदर्भ में सबसे प्रथम शहीद होगा वेगों के योग का नियम। क्योंकि प्रकाश के बैग में आप कोई भी बेग जोड़े, योग प्रकाश का वेग ही होगा। अर्थात् w= u+v समीकरण वैध नहीं रहेगी। इसे बदलना होगा। परन्तु, यह नए नियम का वह रूप होगा जो कमतर वेग पर वैध रहेगा; आखिर इस नियम ने 300 साल तक हमारा साथ दिया है, और यह साधारण तौर पर पाए जाने वाले वेगों के संदर्भ में आगे भी काम देता रहेगा।
अब किसी भी सूचना के प्रसार की अधिकतम गति की सीमा प्रकाश के वेग से परिभाषित होगी। लिहाज़ा घटनाओं को दो समूहों में बांटा जा सकता है। एक समूह उन घटनाओं का होगा जिनके बीच परस्पर कार्य-कारण का सम्बंध है और जिनके बीच समय का अंतराल प्रकाश के एक घटना से दुसरी घटना तक पहुंचने में लगे समय के बराबर या उससे अधिक है। दूसरा समूह उन घटनाओं का है जो कार्य-कारण के लिहाज़ से परस्पर असंबंधित हैं (जिनके बीच समय का अंतराल प्रकाश को एक घटना से दूसरी तक पहुंचने में लगने वाले समय से कम है)। प्रकाश से तेज़ कोई सूचना नहीं पहुंच सकती। अर्थात् एक स्थान से दूसरे स्थान तक 'कारण' के पहुंचने की अधिकतम चाल भी प्रकाश की चाल से अधिक नहीं हो सकती।
चूंकि यह एक ऐसे वेग का अस्तित्व है जिसके बारे में समस्त प्रेक्षक सहमत हैं, अतः यह वेग आकाश व समय को परस्पर जोड़ देगा (इसे भौतिकी में स्पेस-टाइम या दिक्काल का नाम दिया गया है)। हम दूरियों को सेकण्ड में नाप सकते हैं (उतनी दूरी को तय करने में प्रकाश को लगने वाला समय) या समय को सेंटीमीटर में नाप सकते हैं (उतने समय में प्रकाश द्वारा तय की गई दूरी)।
यदि हम दो स्थानों के बीच अलग-अलग रास्तों से यात्रा करें तो हमें अलग-अलग दूरी तय करनी होगी, अर्थात दूरी मार्ग-निर्भर होती है। यह बात हम रोज़मर्रा के अपने अनुभव से जानते हैं। चूंकि प्रकाश के सार्वभौमिक वेग के फलस्वरूप दूरी व समय परस्पर तुल्य हैं इसलिए दो घटनाओं के बीच समय का अंतराल भी मार्ग-निर्भर होगा। अर्थात दो घटनाओं के बीच समय का अंतराल इस बात पर निर्भर करेगा कि कोई प्रेक्षक एक घटना से दूसरी घटना तक। जाने के लिए कौन-सा मार्ग चुनता है। सिद्धांततः यदि एक अंतरिक्ष यात्रा का समय अंतरिक्ष यात्री की घड़ी में पढ़ा जाए और पृथ्वी पर खड़े उसके साथियों की घड़ी में पढ़ा जाए, तो ये समय अंतराल अलग-अलग होंगे क्योंकि इन दो प्रेक्षकों ने दो घटनाओं, यात्रा की शुरुआत व अंत, के बीच अलग-अलग मार्ग अपनाए हैं। यह एक अलग बात है कि यह अंतर कितना कम या अधिक है। एक बार हम यह समझ लें कि दूरी की तरह समय भी मार्ग-निर्भर है तो फिर यह सवाल अर्थ-हीन है कि कौन सी घड़ी सही है। दोनों घड़ी सही हैं और फिर भी अलग-अलग समय बताती हैं; ठीक वैसे जैसे अलग-अलग रास्तों से एक स्थान से दूसरे स्थान तक जाने वाली कारें अलग-अलग किलोमीटर दर्शाएंगी।
यानी प्रकाश व समय दोनों के मापन सापेक्ष व प्रेक्षक यानी अवलोकन-कर्ता पर निर्भर हैं। दरअसल जो चीज़ प्रेक्षक से स्वतंत्र और अपरिवर्तनशील है वह इन दोनों के गठबंधन से प्राप्त दिक्काल (स्पेसटाइम) है। 1908 में अपना प्रख्यात कोलोन व्याख्यान देते हुए मिन्कोस्की ने कहा था, "अपने तई आकाश और अपने तईं समय दोनों ही पृष्ठभूमि में चले जाएंगे और मात्र इन दोनों का एक गठबंधन ही स्वायत्त सत्ता बना पाएगा।" अर्थात् प्रकाश ही आकाश व समय को गुंथकर दिक्का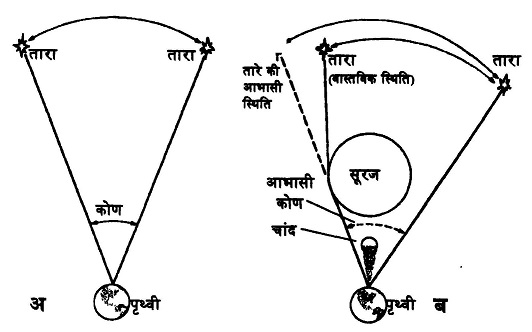
ल (स्पेस-टाइम) का रूप देता है। यह एक नवीन संश्लेषण है।
आकाश को मोड़ता प्रकाश
संहति और ऊर्जा समतुल्य हैं। तो ऊर्जा के किसी भी रूप को वह सब कर सकना चाहिए जो संहति करती है। इसका अर्थ है कि जिस भी चीज़ में ऊर्जा है, उसे गुरुत्व क्षेत्र के साथ अंतर्निया करनी चाहिए। किसी कण की किसी भी क्षेत्र के साथ अंतक्रिया का पता कैसे चलता है? वेग में परिवर्तन को देखकर। मसलन जब किसी कण को उछाला जाता है तो पृथ्वी के गुरुत्वाकर्षण के विरुद्ध चलते हुए उसका वेग लगातार कम होता जाता है। जब प्रकाश में ऊर्जा है तो उसे भी ऐसा ही करना चाहिए। किन्तु प्रकाश की प्रकृति यह है कि उसका वेग तो कम नहीं हो सकता। इसका वेग तो एक सार्वभौमिक स्थिरांक है, वह कभी नहीं बदलता। फिर प्रकाश गुरुत्वाकर्षण को कैसे महसूस करेगा?
इसका मतलब यह निकलता है कि यदि प्रकाश की अंतक्रिया गुरुत्वाकर्षण से होनी है, तो हमें बुनियादी रूप से कुछ नया करना होगा। तब प्रासंगिक सबाल यह है कि वह क्या है जिसके प्रति प्रकाश प्रत्युत्तर दे सके।
प्रकाश आकाश में एक तरंग के रूप में गमन करता है। अतः यह मात्र आकाश (स्पेस) में परिवर्तन का प्रत्युत्तर दे सकता है। एकमात्र सूझ-बूझ से भरी बात यह होगी कि गुरुत्वाकर्षण आकाश में वक्रता उत्पन्न करे और प्रकाश इस वक्र आकाश के समांतर चले। वक्रता के समांतर चलना ही वक्र आकाश पर सबसे सीधा मार्ग होगा।
प्रकाश का मुड़ना: सूरज के ठीक पीछे मौजूद तारे का प्रकाश जब सूरज के पास से गुज़रता है तो गुरुत्वाकर्षण की वजह से प्रकाश अपने मार्ग से विचलित हो जाता है और प्रकाश किरण थोड़ी सी मुड़ जाती है। लेकिन किरणों के मुड़ने की जांच सिर्फ पूर्ण सूर्य ग्रहण के दौरान ही हो सकती थी। आइंस्टाइन ने बहुत पहले ही इस घटना की भविष्यवाणी की थी परन्तु 1919 और 1922 को हुए पूर्ण सूर्य ग्रहण के समय की गई जांच के दौरान ही इस तथ्य की सत्यता साबित हो सकी। इस जांच के लिए किया यह गया कि सूर्य ग्रहण के दौरान सूर्य के ठीक पीछे रहने वाले तारा मंडल की तस्वीर ऐसे समय खींच ली गई जब उससे आती हुई रोशनी को सूरज के आसपास से न गुज़रना पड़े। देखिए चित्र 'अ'। फिर पूर्ण सूर्य ग्रहण के दौरान जब सूरज की पूरी चकती को चांद ने ढक लिया, तब सूरज के पास दिख रहे उसी तारा मंडल की तस्वीर फिर से ली गई। देखिए चित्र 'च'। दोनों तस्वीरों का मिलान किया जिस से समझ में आया कि ग्रहण के दौरान तारों की स्थिति कुछ हटकर दिख रही है, यानी सूरज के पास से गुजरते हुए इन तारों का प्रकाश विचलित हुआ था। या दूसरे शब्दों में गुरुत्वाकर्षण के कारण प्रकाश के पथ पर प्रभाव पड़ा था और वह थोड़ा सा मुड़ गया था।
चित्रः 'स' 1922 के पूर्ण सूर्यग्रहण के बाद अल्बर्ट आइंस्टाइन को किया गया टेलीग्राम जिसमें ग्रहण के दौरान किए गए अवलोकनों की पुष्टि की गई।
किसी गोले की सतह पर सबसे सीधा रास्ता एक वृत्त होता है जिसका केन्द्र गोले का केन्द्र हो। किसी भी वक्र सतह पर सरल रेखा के लिए तकनीकी शब्द 'जियोडेसिक' है, और यह मात्र किसी समतल सपाट सतह पर ही ‘सरल रेखा' के रूप में दिखाई देती है। इसका गुण यह होता है कि यह किन्हीं दो बिन्दुओं के बीच चरम-मान (एक्स्ट्रीमल, सबसे छोटा या सबसे बड़ा) वाला मार्ग दर्शाती है।
गुरुत्वाकर्षण से अंतक्रिया के दौरान अपेक्षा यह होती है कि अन्य कणों की तरह प्रकाश भी सरल रेखा में गति करने की बजाए मुड़ जाएगा। यही प्रभाव तब भी हासिल हो सकता है जब प्रकाश की बजाए आकाश (स्पेस) को मोड़ दिया जाए। अतः समस्त प्रासंगिक सिद्धांतों की भौतिक सुसंगति के लिए अनिवार्य है कि गुरुत्वाकर्षण आकाश में वक्रता उत्पन्न करे। यानी विशाल गुरुत्वीय पिण्ड अपने आसपास के आकाश में वक्रता उत्पन्न करेंगे। यदि विशिष्ट सापेक्षता को ध्यान में रखें तो आकाश की वक्रता का अर्थ होगा दिक्काल (स्पेस-टाइम) की वक्रता। यानी प्रकाश गुरुत्वाकर्षण से तभी अंतक्रिया कर सकता है जब वह दिक्काल (स्पेस-टाइम) में वक़्ता उत्पन्न करे। दूसरे शब्दों में, प्रकाश आकाश को मोड़ता है।
यानी गुरुत्व दोहरी भूमिका निभात है - वह कणों में त्वरण उत्पन्न करता है और दिक्काल में बक्रता उत्पन्न करता है ताकि प्रकाश उसे महसूस कर सके। निहितार्थ यह है कि मुड़ता आकाश है, प्रकाश नहीं। 1919 में पूर्ण सूर्य ग्रहण के दौरान पहली बार एडिंगटन के दल ने जो चीज़ देखी थी वह प्रकाश का मुड़ना नहीं था। वह दरअसल आकाश का मुड़ना था। यह लगभग वैसा ही है जैसे हम रोज़ाना सूरज को पूर्व से पश्चिम की ओर जाता देखते हैं मगर सच्चाई यह है कि पृथ्वी घूम रही है।
अर्थात गुरुत्वाकर्षण को मात्र दिक्काल (स्पेस-टाइम) की वक्रता के रूप में ही परिभाषित किया जा सकता है। इसे संभव बनाने वाला सिद्धांत है सामान्य सापेक्षता।
सपाट से वक्र तक
एक महत्वपूर्ण बात यह है कि कोई भी सार्वभौमिक गुण या कथन ज्यामितीय रूप में व्यक्त करने योग्य होना चाहिए। जैसे कि बल की अनुपस्थिति में प्रकाश के वेग और कण की मुक्त गति के लिए मिन्कोव्स्की की मेट्रिक्स है। आगे यह हमारे लिए एक अच्छा मार्गदर्शक सिद्धांत होगा।
बल के मापन के लिए हमें यथार्थ में एक जड़त्वीय फ्रेम (Inertial frame) चाहिए। सवाल यह है कि इसे यथार्थ में प्राप्त कैसे किया जाए। सारे बलों
प्रिंट गैलरीः प्रख्यात चित्रकार एम. सी. एशर की एक पेंटिग जिसमें नॉन-यूक्लिडियन ज्यामिती की विभिन्न संभावनाएं नज़र आती हैं।
को हटाना पड़ेगा। प्रकृति में चार प्रकार के बल होते हैं। इनमें से दो बल तो कम दूरी के बल हैं। अतः ये विस्तृत क्षेत्र में नहीं लगते। अन्य दो बल लंबी दूरी के बल हैं। इनमें से विद्युत चुंबकीय बल तो मात्र विद्युत आवेश युक्त कणों से जुड़ा है। आवेशों व धाराओं का उपयुक्त वितरण स्थापित करके इस बल को बाहर रखा जा सकता है।
किन्तु गुरुत्वाकर्षण का बल सार्वभौमिक है और इसे रोका नहीं जा सकता। स्वयं न्यूटन ने भी गुरुत्व बल को हटाने सम्बंधी कठिनाई को पहचाना था। उनका सुझाब यह था कि जड़त्वीय फ्रेम को साकार करने के लिए सारे पदार्थ से अनंत दूरी पर जाना होगा।
चूंकि गुरुत्व को ब्रह्माण्ड के स्तर पर हटाना असंभव है, इसलिए एक ब्रह्माण्डीय जड़त्वीय फ्रेम भी असंभव है। अलबत्ता इसे स्थानविशेष से हटाया जा सकता है, जैसा कि गैलीलियो द्वारा पीसा की मीनार पर किए गए प्रसिद्ध प्रयोग से पता चलता है। समस्त कणा में दो गुण समान होते हैं: जड़त्व और गुरुत्वाकर्षण से जुड़ाव (गुरुत्वीय आबेश)। समस्त कणों के लिए एकमात्र सार्वत्रिक मापक संहति (ऊर्जा) है। अर्थात् जड़त्व और गुरुत्वीय आवेश, दोनों का मापक एक ही होना चाहिए। इसका अर्थ यह होगा कि गुरुत्व के प्रभाव से सारे कण एक समान त्वरण से गिरेंगे और इस पर कण की संहति, आकृति और पदार्थ का कोई असर नहीं होगा। गैलीलियो ने प्रयोग द्वारा इसी बात का सत्यापन किया था।
आइंस्टाइन के अनुसार गुरुत्व को हटाने का तरीका यह होगा कि आप स्वतंत्र रूप से गिरती एक लिफ्ट के साथ अपने आपको गिरने दें। खुश-किस्मती की बात यह है कि गैलीलियो के विपरीत आइंस्टाइन ने यह प्रयोग वास्तव में न करके मात्र ख्यालों में किया, वरना वे हमें इसके परिणाम बताने की स्थिति में न होते। और न ही सामान्य सापेक्षता की कहानी आगे बढ़ती।
स्वतंत्र रूप से गिरती लिफ्ट वाकई जड़त्वीय फ्रेम की द्योतक है किन्तु मात्र स्थानीय स्तर पर। अर्थात् हम कहीं भी एक स्थानीय जड़त्वीय फ्रेम (Local Inertial Frame) निर्मित कर सकते हैं, ब्रह्माण्डीय जड़त्वीय फ्रेम (Global Inertial Frame) नहीं। सापेक्षता का सिद्धांत कहता है कि समस्त स्थानीय जड़त्वीय फ्रेम समतुल्य हैं और इसे समतुल्यता का सिद्धांत कहा जाता है। इसका मतलब यह है कि वास्तविक या ख्याली, कोई भी प्रयोग करके दो स्थानीय जड़त्वीय फ्रेम के बीच भेद करना असंभव है।
आप स्थानीय स्तर पर गुरुत्व उत्पन्न भी कर सकते हैं। करना यह होगा कि मुक्त आकाश में किसी लिफ्ट को ऊपर की दिशा में गुरुत्व के बराबर त्वरण प्रदान कर दिया जाए। यह स्थिति लिफ्ट के अंदर की उस स्थिति से अलग न होगी जब वह विराम की अवस्था में धरातल पर हो। समतुल्यता सिद्धांत का ज्यादा स्पष्ट वक्तव्य यह होगाः समस्त स्थानीय जड़त्वीय फ्रेम, दिक्काल (स्पेसटाइम) में उनकी स्थिति चाहे कुछ भी हो, सार्वभौमिक स्थिरांकों - प्रकाश का वेग, गुरुत्व स्थिरांक और प्लान्क स्थिरांक - का मूल्य बराबर नापेंगे।
ब्रह्माण्डीय जड़त्वीय फ्रेम का अस्तित्व न होने के निहितार्थ अत्यंत व्यापक हैं कि ब्रह्माण्ड के स्तर पर दिक्काल (स्पेस-टाइम) वक़ होना चाहिए। यह बात यूक्लिडीय दूरियों और रीमेनीय दूरियों के अंतर के रूप में सामने आती है। स्थानीय रूप से हम आज भी यूक्लिडीय दूरियों का इस्तेमाल कर सकते हैं। मसलन धरती की सतह पर। हम छोटे पैमाने की दूरियां पता करने के लिए तो यूक्लिडीय ज्यामिति का इस्तेमाल करते हैं - जैसे पुणे से मुंबई की दूरी। दूसरी ओर, मुंबई से लंदन की दूरी के लिए इसका
समतुल्यता: भौतिक विज्ञान के नियम दोनों स्थितियों में समान होंगे - (अ) मुक्त अंतरिक्ष में रॉकेट को ऊपर की दिशा में गुरुत्व के बराबर त्वरण प्रदान कर दिया जाए; या (ब) रॉकेट धरातल पर यानी पृथ्वी के गुरुत्वाकर्षण क्षेत्र में स्थिर खड़ा हो।
उपयोग नहीं किया जा सकता।
मुक्त कण की गति वक्र ज्यामिति की 'सरल रेखा' से परिभाषित होती है। गौरतलब है कि एक गोले की सतह पर 'सरल रेखा' वह वृत्त होता है जिसका केन्द्र गोले का केन्द्र हो। अर्थात् गुरुत्व पूरी तरह दिक्काल (स्पेस-टाइम) की ज्यामिति में अंगीकार हो चुका है। और उसी की वक्रता से परिभाषित होता है। इससे हम आइंस्टाइन के गुरुत्वाकर्षण के सिद्धांत पर पहुंचते हैं, जिसका नाम है सामान्य सापेक्षता।
(अगले अंक में जारी)
नरेश दधीच: पुणे के इंटर यूनिवर्सिटी सेंटर फॉर एस्ट्रोनॉमी एंड एस्ट्रोफिजिक्स (IUCAA) में खगोल विज्ञान में शोधकार्य कर रहे हैं। इस संस्थान को बनाने में उनकी विशेष भूमिका रही है।
अनुवाद - सुशील जोशीः एकलब के होशंगाबाद विज्ञान शिक्षण कार्यक्रम से जुड़े हैं। स्वतंत्र रूप से विज्ञान लेखन एवं अनुवाद करते हैं।
यह लेख 'इंडियन एसोसिएशन फॉर जनरल रिलेटिविटी एंड ग्रेविटेशन' (IAGRG) द्वारा आयोजित एक व्याख्यान माला में, नरेश दधीच द्वारा दिए गए व्याख्यान पर आधारित है। यह आयोजन 30 जनवरी, 2001 को नागपुर में किया गया था। यह व्याख्यान माला एसोसिएशन के दो वरिष्ठतम सदस्यों प्रोफेसर पी, सी. वैद्य एवं ए. के. रायचौधरी के सम्मान में आयोजित की जाती है। इससे पहले के छह व्याख्यान एन, मुकुंदा, जे. बी. नारळीकर, एन, पंचपकेशन, सी. बी. विश्वेश्वरा, आर. कौशिक और एस. एम. चित्रे द्वारा दिए गए थे।