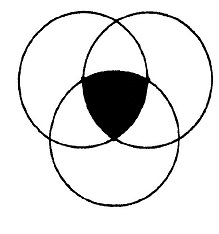
 पिछले अंक में आपसे जो सवाल पूछा गया था उसमें तीन वृत्त बने थे जिनकी परिधि एक दूसरे वृत्त के केन्द्र से होकर गुजर रही थीं। और आपको बताना था कि इन तीनों वृत्तों द्वारा एक-दूसरे को ढांकने से बना शेडेड भाग किसी भी एक वृत्त के चौथाई हिस्से से बड़ा है या छोटा। सवाल का जवाब आप किसी गणितीय विधि से दे सकते थे, या किसी तर्क के आधार पर।
पिछले अंक में आपसे जो सवाल पूछा गया था उसमें तीन वृत्त बने थे जिनकी परिधि एक दूसरे वृत्त के केन्द्र से होकर गुजर रही थीं। और आपको बताना था कि इन तीनों वृत्तों द्वारा एक-दूसरे को ढांकने से बना शेडेड भाग किसी भी एक वृत्त के चौथाई हिस्से से बड़ा है या छोटा। सवाल का जवाब आप किसी गणितीय विधि से दे सकते थे, या किसी तर्क के आधार पर। 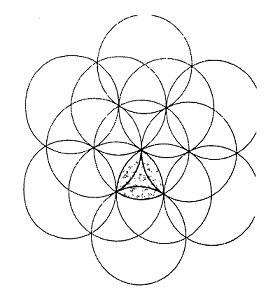 इस सवाल के कई जवाब मिले हैं। कुछ पाठकों का मानना है कि चित्र को देखकर ही यह आभास होता है कि शेडेड़ भाग किसी भी एक वृत्त के चौथाई हिस्से से कम महसूस होता है। कुछ पाठकों ने रेखागणित की मदद से बताया कि शेडेड भाग वृत्त के चौथाई भाग से कम है। ऐसा ही एक तरीका हम यहां सुझा रहे हैं।
इस सवाल के कई जवाब मिले हैं। कुछ पाठकों का मानना है कि चित्र को देखकर ही यह आभास होता है कि शेडेड़ भाग किसी भी एक वृत्त के चौथाई हिस्से से कम महसूस होता है। कुछ पाठकों ने रेखागणित की मदद से बताया कि शेडेड भाग वृत्त के चौथाई भाग से कम है। ऐसा ही एक तरीका हम यहां सुझा रहे हैं।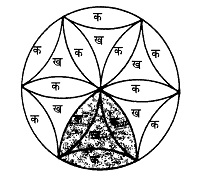 इस हल के लिए सबसे पहले शेडेड हिस्से को बनाने वाले किसी एक वृत्त में से होकर गुजरने वाले और एक-दूसरे को काटने वाले कई और वृत्त खींचते हैं, जिससे पिछले पृष्ठ पर दिए गए चित्र जैसा पैटर्न बनकर उभरता है। इस पैटर्न में से एक वृत्त व शेडेड भाग, यहां दिखाया गया है।
इस हल के लिए सबसे पहले शेडेड हिस्से को बनाने वाले किसी एक वृत्त में से होकर गुजरने वाले और एक-दूसरे को काटने वाले कई और वृत्त खींचते हैं, जिससे पिछले पृष्ठ पर दिए गए चित्र जैसा पैटर्न बनकर उभरता है। इस पैटर्न में से एक वृत्त व शेडेड भाग, यहां दिखाया गया है।
इस चित्र में आप देखेंगे कि वृत्त 6 डेल्टा आकृतियों 'ख' और 12 केलेनुमा आकृतियों 'क' से मिलकर बना है।
अब घोडेड हिस्से को देखिए। यहां तीन केलेनुमा और एक डेल्टा आकृति मौजूद है। जबकि वृत्त के चौथाई हिस्से में डेढ़ डेल्टा आकृति और तीन केलेनुमा आकृति का होना जरूरी होगा। इस हिसाब से भी शेडेड भाग वृत्त के एक चौथाई से कम है।
एक हल गणितीय विधि से - 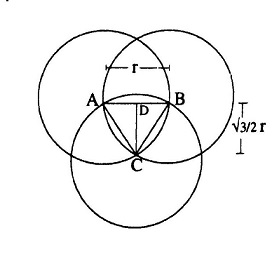 यहां तो हमने जवाब का एक तरीका बताया है। हमारे पाठकों ने इस सवाल को हल करने के लिए रेखागणित की विधि का इस्तेमाल किया है। यहां एक जवाब दे रहे हैं - जिसे विनय शर्मा, जबलपुर ने भेजा है। जवाब इस तरह हैः
यहां तो हमने जवाब का एक तरीका बताया है। हमारे पाठकों ने इस सवाल को हल करने के लिए रेखागणित की विधि का इस्तेमाल किया है। यहां एक जवाब दे रहे हैं - जिसे विनय शर्मा, जबलपुर ने भेजा है। जवाब इस तरह हैः
कोई तार्किक हल तो नहीं सुझा लेकिन जो सुझ पड़ा उसे भेज रहा हूं। प्रश्न में पूछे गए शेडेड भाग के तीनों केन्द्रों को मिलाने पर त्रिभुज A B C प्राप्त हुआ। जो कि एक समबाहु त्रिभुज है, माना इसकी एक भुजा r है।
अतः माध्यिका
CD = AB Sin/60
= r √3/2
त्रिभुज ABC का क्षेत्रफल = 1/2 आधार गुना
ऊंचाई
= 1/2 AB x CD
= 1/2 x √3/2 x r2 पुनः प्रश्न में दिए गए शेडेड भाग से त्रिभुज निकालने के बाद चित्र (ख) में दिखाई आकृति AMB का क्षेत्रफल निकालने पर।
पुनः प्रश्न में दिए गए शेडेड भाग से त्रिभुज निकालने के बाद चित्र (ख) में दिखाई आकृति AMB का क्षेत्रफल निकालने पर।
AMB का क्षेत्रफल
= AMBC - त्रिभुज (ABC) का क्षेत्रफल
चूंकि AMBKC वृत्त c के क्षेत्रफल का छठा भाग है।
इसलिए
क्षेत्रफल AMB = (πr×r)/6-√3/4r×r
= (0.524 - 0.443)
= 0.081 r2
अब शेडेड भाग का क्षेत्रफल = त्रिभुज ABC का क्षेत्रफल + 3 x (AMB) का क्षेत्रफल
= 0.443 r2 +3×0.081 r2
= 0.686r2 .....(1)
चूंकि वृत्त के चौथाई हिस्से का क्षेत्रफल = ¼ πr2
= 0.786 r2 . . . . . (2)
समीकरण एक व दो से सिद्ध होता है कि दिए गए शेडेड भाग का क्षेत्रफल वृत्त के 1/4 से कम है।
इनके जवाब भी सही थे: गणितीय विधि से इस सवाल को सही हल करने वाले हमारे पाठकों के नाम इस तरह से हैं - अलका कालरा, रमेश नगर, नई दिल्ली। पूर्वा उमरेकर, गौतम नगर, भोपाल ने भी सहज विधि से हल निकाला है।
इस बार के सवाल
सवालीराम
सवालीराम से पूछे गए सवाल इस तरह से हैं:
1. छुईमुई के पौधे को छूने पर उसकी पत्तियां क्यों सिकुड़ जाती है? दूसरे पौधे ऐसा क्यों नहीं करते?
--ओमप्रकाश, खाचरौद, उम्मैन (म. प्र.)
2. भारत में ऋतुएं क्यों बदलती हैं?
--मंजय कुमार कुशवाह, होशंगाबाद (म. प्र.)
सवालीराम के सवालों में से एक या दोनों सवालों के सही जवाब देनेपर आपको एक पुस्तक उपहार स्वरूप दी जाएगी।
जरा सिर खुजलाइए
1. एक व्यक्ति वर्ष 40 ईसा पूर्व के सातवें दिन पैदा हुआ और ईस्वी सन् 40 के सातवें दिन मर गया। बताइए वह व्यक्ति कितने बरस जिंदा रहा।
2. एक कार चालक ने अपनी कार में एक अतिरिक्त टायर रखते हुए अपना सफर शुरू किया। उसने हर टायर को बारी-बारी से एक जैसा आराम दिया। इस तरह सभी टायर बराबर की दूरी चले। उस व्यक्ति ने कुल 5000 किलोमीटर का सफर किया तो हर टायर ने चलते हुए कितनी दूरी तय की होगी।
3. पांच माचिस की तीलियों का इस्तेमाल करते हुए एक घन बनाने की कोशिश कीजिए। ध्यान रहे माचिस की तीलियों को तोड़ना नहीं है।
अगर आपके पास इन सवालों के जवाब हैं तो कृपया हमारे पास जल्द-से-जल्द भेजिए। हमारा पता आप जानते ही हैं।


