आमोद कारखानिस
विवेक मोंटेरो, नवनिर्मिती के लेख पर आधारित
दुनिया में कुछ प्रयोग ऐतिहासिक होते हैं। ऐसे ही ऐतिहासिक खगोलीय प्रयोगों में से कुछ प्रयोग जिनके जरिए सूर्य से पृथ्वी की दूरी की पहली बार गणना की गई थी, उन्हें सरल ढंग से करने के तरीके यहां सुझाए गए हैं, बिना किन्हीं विशेष उपकरणों के।
मैं जानता हूं कि आपको यह शीर्षक देखकर हैरानी होगी -- परन्तु न एक पत्थर और एक धागे के टुकड़े से बहुत ही कारगर खगोलीय प्रयोगशाला उपलब्ध हो जाती है। आपको लग रहा होगा कि मैं मज़ाक कर रहा हूँ परन्तु रुकिए मुझे थोड़ा समझाने दीजिए।
जब भी विज्ञान की बात होती है, हमारे सामने प्रयोगों और प्रयोगशालाओं की छवि आ खड़ी होती है। जैसे अगर भौतिकशास्त्र की बात करें - अगर हमें इस बात का अध्ययन करना है कि कांच में से गुजरने से प्रकाश के व्यवहार पर क्या असर पड़ता है तो हम क्या करते हैं? एक कांच का गुटका और प्रकाश का स्रोत लेकर हम चाहें वैसे प्रयोग अपनी कक्षा या प्रयोगशाला में कर सकते हैं। परन्तु खगोल शास्त्र एक अलग ही तरह का विज्ञान है। यह तारों और ग्रहों जैसे सुदूर और विशाल खगोलीय पिंडों का विज्ञान है। अगर आप पृथ्वी से सूर्य की दूरी नापना चाहते हैं तो कोई तरीका नहीं है कि सूर्य पर जाकर, एक इतनी बड़ी टेप या मापपट्टी लेकर यह दूरी नाप पाएं जैसे कि आप एक छड़ी या मेज़ की लंबाई मापते हुए करते हैं। तो हम खगोलीय प्रयोगशाला में आखिर करते क्या हैं. प्रयोग कैसे करते हैं? एक खगोल शास्त्री केवल अवलोकन कर सकता है। किन चीज़ों के अवलोकन कर सकता है वह - इसकी भी सीमाएं हैं।
खगोलशास्त्र में आप केवल कोण और समय माप सकते हैं। हम दूरियां नहीं नाप सकते परन्तु यह जरूर पता कर सकते हैं कि हम जहां खड़े हैं वहां से देखने पर दो तारे आपस में कितने अंश का कोण बना रहे हैं, या पृथ्वी से देखने पर सूर्य की चकती कितने अंश का कोण बनाती है; या फिर हम यह नाप सकते हैं कि एक निश्चित समय में किसी तारे ने कितनी कोणीय दूरी तय की है यानी कितना खिसका वह अपने पहले स्थान से। इसलिए खगोलीय प्रयोगशाला बनाने के लिए हमें ऐसे साधनों की जरूरत होगी जिनका इस्तेमाल हम कोण या समय नापने के लिए कर सकते हैं। इसी वजह से पत्थर और धागे का टुकड़ा हमारे काम आएंगे।
इतने सशक्त उपकरणों के बारे में बिना किसी उदाहरण के बात करने में कोई मज़ा नहीं है इसलिए क्यों न खगोलशास्त्र की एक अत्यंत महत्वपूर्ण दूरी का उदाहरण लेकर बात शुरू करें - यह देखने की कोशिश करें कि पृथ्वी से सबसे नज़दीकी और सबसे परिचित तारे तक की दूरी हम कैसे नाप सकते हैं? यह सवाल साधारण-सा लग सकता है। परन्तु है वैसा नहीं। विज्ञान को इसे नापने और एक सटीक उत्तर तक पहुंचने में काफी लंबा अर्सा लग गया।
बहुत समय पहले ईसा पूर्व पांचवीं सदी में किसी समय ग्रीक विद्वान एनेक्सेगोरस शायद उन शुरुआती लोगों में से था जिसने इस दूरी को मापने की कोशिश की। यह समय था जब ग्रीक विद्वान ज्यामिती को व्यवस्थित करने की कोशिशों में लगे हुए थे। जैसा कि हम सबै अब जानते हैं कि मानव के इतिहास में ज्यामिती की शुरुआत जमीन नापने के तरीके विकसित करते हुए हुई।
एनेक्सेगोरस को यह विचित्र ख्याल आया कि ब्रह्मांड को मापने के लिए ज्यामिती और खगोलशास्त्र को मिला देना चाहिए। वह सूर्य की पृथ्वी से दूरी व सूर्य का व्यास दोनों नापना चाहता था। उसने यह जानने के लिए एक तरीका भी निकाल लिया और उत्तर भी प्राप्त कर लिया कि पृथ्वी और सूर्य की दूरी 6500 किलोमीटर है और सूर्य का व्यास 60 किलोमीटर है।
आज हम जानते हैं कि ये दोनों जवाब गलत हैं परन्तु फिर भी एनेक्सेगोरस शायद पहला व्यक्ति था जिसने यह प्रयास किया था। उसके जवाब इसलिए गलत नहीं थे क्योंकि उसका तरीका गलत था। बस गलत थी तो उसकी एक मान्यता। परन्तु हम पटरी से उतरने लगे हैं। इसलिए चलिए हम अपनी बात पर लौटते हैं - एनेक्सेगोरस की कोशिश के बारे में और जानकारी के लिए आप अगले पृष्ठ पर दिया गया बॉक्स देख सकते हैं।
आप सबने सूर्य देखा है। हमें मालूम है कि सूर्य एक गोल चकती जैसा दिखता है। परन्तु यह चकती बड़ी कितनी है? आप सूर्य की तरफ सीधे देख नहीं सकते। ऐसा करने से आंखों को नुकसान पहुंच सकता है, इसलिए चकती का आकार नापना मुश्किल है। इस वजह से हम चकती की छवि हासिल करके, उसका आकार नापकर देखेंगे कि उससे इस चकती के आकार के बारे में हम कुछ कह सकते हैं क्या?
सूर्य की छवि कैसे प्राप्त करें?
आपने पिनहोल केमरा के बारे में ज़रूर पढ़ा होगा। हम उसी सिद्धांत का इस्तेमाल करके सूर्य की छवि हासिल करेंगे। इस प्रयोग के लिए मोटी कार्डशीट या फिर पोस्टकार्ड की जरूरत होगी। इस कार्डशीट या पोस्टकार्ड में एक छेद बना लीजिए - लगभग आधा सेंटीमीटर व्यास का सुराख ठीक रहेगा (पेपर पंच से लगभग इसी साइज़ का छेद बनता है)। उसी के पास बड़े व्यास का एक और छेद बनाइए। इस कागज़ को सूर्य के सामने इस तरह से पकड़े कि उसकी छाया दीवार पर बने।
| एनेक्सेगोरस का प्रयोग और एक चूक एनेक्सेगोरस पहला ग्रीक वैज्ञानिक था जिसने खगोलीय अवलोकनों के लिए ज्यामिती की अवधारणाओं का इस्तेमाल किया और खगोलीय दूरियां मापने की कोशिश की। यहां पर उसका एक अत्यन्त महत्वपूर्ण परन्तु आसान व मजेदार प्रयोग दे रहे हैं। एनेक्सेगोरस को मालूम था कि ग्रीक साम्राज्य के कुछ इलाकों में किन्हीं विशेष दिन सूर्य किरणों से छाया नहीं बनती थी। यानी कि उन स्थानों पर उस दिन सूर्य एकदम सिर के ऊपर रहता है। अब हमें मालूम है कि यह इलाका मकर और कर्क रेखा के बीच में आता है। उसने दो शहर और अपने सबसे विश्वसनीय लोग इस प्रयोग को करने के लिए चुने। उसे मालूम था कि पहले शहर में एक खास दिन, एक खास समय सूर्य किरणों से खंभे की छाया नहीं बनती थी। उस दिन उसी समय अगर आप दूसरे शहर में एक ऐसे ही खंभे का अवलोकन करें तो उसकी छाया मौजूद होती थी। उसने छाया की लंबाई नापी और फिर साधारण ज्यामिति का इस्तेमाल करते हुए सूर्य की दूरी ज्ञात की। सामने वाले चित्र को देखिए--- खंभे और छाया द्वारा बनाई गई त्रिभुज और सूर्य व दोनों शहर द्वारा बनाई गई त्रिभुज दोनों समरूप हैं इसलिए: (खंभे की ऊंचाई)/(खंभे की छाया की लंबाई ) = (सूर्य-पृथ्वी दूरी )/(दोनों शहरों के बीच की दूरी ) इस गणना के आधार पर उसने सूर्य-पृथ्वी की दूरी का मान 6500 कि.मी. |
अगर आप यह प्रयोग सुबह या शाम को करें तो दीवार पर छाया बना पाना आसान होगा। दीवार पर बन रही छवि को नापना आसान होता है। कागज़ इस तरह पकड़ना होगा कि उसकी छाया और आपने जो छेद बनाया है, दोनों आपको स्पष्ट दिखाई दें। सुनिश्चित कीजिए कि छवि का आकार ठीक वैसा हो जैसा छेद का था, यानी कि दीवार या पर्दा सूर्य किरणों के लंबवत हो और कागज़ दीवार के समानान्तर हो।
अब कोण बदले बिना कागज़ को धीरे-धीरे दीवार से दूर लेकर जाइए। आपको क्या दिखता है?
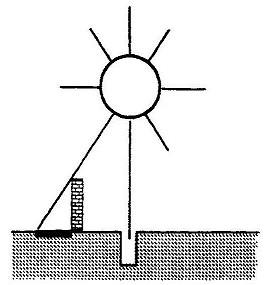 पाया। आज हमें मालूम है कि यह जवाब सही नहीं है। सवाल है कि उसने क्या गलती की? पाया। आज हमें मालूम है कि यह जवाब सही नहीं है। सवाल है कि उसने क्या गलती की? उसके अवलोकन सही थे, उसने दूरियां भी काफी सटीकता से नापी, इसके बावजूद कि उन दिनों दो शहरों के बीच की दूरी मापना काफी कठिन काम था। उसके सिद्धान्त में कोई गलती नहीं थी, न ही अवलोकनों में; परन्तु चूक थी एक मान्यता में जिस पर सिद्धांत आधारित था। चित्र को फिर से देखें। यह ठीक वैसे ही बनाया गया है जिस तरह से एनेक्सेगोरस ने कल्पना की थी। आपको भी शायद गलती दिख गई होगी - इस चित्र में दोनों शहरों को एक सरल रेखा जोड़ रही है जबकि पृथ्वी की सतह सपाट नहीं है। अगर उसने धरती की गोलाई को ध्यान में लेते हुए गणनाओं में सुधार किया होता तो उसे कहीं बेहतर परिणाम मिलता। परन्तु मजेदार बात यह है कि अपने सवाल का हल ढूंढने के बजाय उसने इस प्रक्रिया में किसी दूसरे ही सवाल का जवाब ढूंढ लिया था। दरअसल 6500 किमी का यह आंकड़ा पृथ्वी की त्रिज्या है जो उसने अनजाने में ढूंढ निकाली थी। इरेटोसथिनस ने दो सौ साल बाद यानी ईसा पूर्व तीसरी सदी में, धरती को गोलाकार मानते हुए इसी प्रयोग से पृथ्वी की त्रिज्या का पता लगाया। लेकिन पृथ्वी से सूर्य की दूरी पता करने में अभी और लंबा सफर तय होना था। |
जब मैंने इस प्रयोग को करके देखा तो मेरे अवलोकन कुछ इस प्रकार थेः
क - जैसे-जैसे दूरी बढती या घटती है, तो गोल छवियों को आकार भी बड़ा-छोटा होता है।
ख - एक विशेष दूरी के बाद दोनों छवियों का आकार (साइज़) लगभग बराबर बना रहता है।
ग - इस स्थिति में एक छवि, दूसरी छवि से चमकीली जरूर होती है, परन्तु दोनों का आकार लगभग बराबर होता है।
पृथ्वी-सूर्य की दूरी और सूर्य के व्यास में संबंध
इन अवलोकनों के आधार पर हम कुछ मापन करेंगे। शुरुआत कागज़ को दीवार से तीन मीटर दूर रखते हुए नाप लेकर कर सकते हैं। इस स्थिति में छवि का व्यास माप लें। अब कागज़ और दूर लेकर जाएं। लगभग 5 मीटर की दूरी पर कागज़ रखकर छवि के व्यास का नाप फिर से दोहराएं। हर बार आपको कागज से छाया (दीवार) की दूरी मापनी है, और 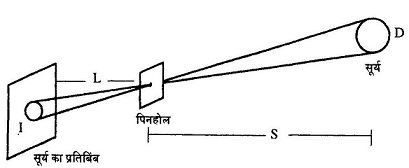 छवि का आकार मापना है। अगर आपको लगे कि कागज़ में छेद का आकार इतना छोटा है कि आप ठीक से माप नहीं ले पा रहे तो आप छत या खिड़की के किसी छेद को अपना पिन होल मानकर, छेद से छवि की दूरी और छवि का व्यास माप सकते हैं।
छवि का आकार मापना है। अगर आपको लगे कि कागज़ में छेद का आकार इतना छोटा है कि आप ठीक से माप नहीं ले पा रहे तो आप छत या खिड़की के किसी छेद को अपना पिन होल मानकर, छेद से छवि की दूरी और छवि का व्यास माप सकते हैं।
मैं कोई बाजीगर नहीं हूँ परन्तु फिर भी आपसे इतना दूर रहते हुए भी, मुझे मालूम है कि आपका माप क्या आएगा!
संभवतः दूरी और व्यास के अनुपात के बारे में आपका जवाब छेद के आकार, साइज़, प्रयोग की तारीख व समय से पूर्णतः स्वतंत्र है। वह होगा -- 1 1 0
मैं आपके नाप के बारे में इतने आत्मविश्वास से कैसे कह पा रहा हूं, इसे समझने के लिए आइए साधारण स्कूलीय ज्यामिती को याद करें। नीचे बनाए चित्र पर एक नजर डालें। क्या यह चित्र आपके द्वारा किए गए प्रयोग को प्रदर्शित करता है? ध्यान रहे कि यह चित्र अनुपातिक नहीं है।
आइए यह मान लें कि ---
I = छवि यानी प्रतिबिंब का व्यास
L = कागज़ से दीवार पर बने प्रतिबिंब की दूरी
S = सूर्य और पृथ्वी के बीच की दूरी
D = सूर्य का व्यास चूंकि एक-दूसरे को काट रही दो सरल रेखाओं के दोनों विपरीत कोण समान होते हैं इसलिए हम देख सकते हैं कि दोनों त्रिभुज समरूप हैं।
इसलिए L/I = S/D
क्योंकि आपके द्वारा मापी गई दूरियों का अनुपात S/D के बराबर होने वाला है, और चूंकि S व D दोनों नाप निश्चित हैं, इसीलिए मैं पक्के तौर पर कह सकता हूं कि आपके अवलोकन भी मेरी गणनाओं के बराबर ही होंगे, जो कि लगभग 110 को अनुपात बताती हैं।
इसलिए हमें जो पहली जानकारी प्राप्त होती है वह इस प्रकार हैः
L/I = S/D~ 110 ............... (1)
इसका अर्थ है कि सूर्य के व्यास की तुलना में, वह पृथ्वी से 110 गुना ज्यादा दूर है।
हमारा मकसद था कि हम सूर्य की पृथ्वी से दूरी पता करें। इस समीकरण से हमें यह दूरी सूर्य के व्यास के रूप में प्राप्त हो गई है। अब हमें बस सूर्य के व्यास का पता लगाना है! इसे कैसे मापें?
शुक्र से सूर्य कितना बड़ा - ग्रहण से मिलेगा जवाब
आमतौर पर कोई भी दूरी नापने के लिए हम स्केल या टेप को इस्तेमाल करते हैं। परन्तु सूर्य के आकार की कोई चीज़ मापने के लिए। हमारा पैमाना या यंत्र भी उतना ही विशाल 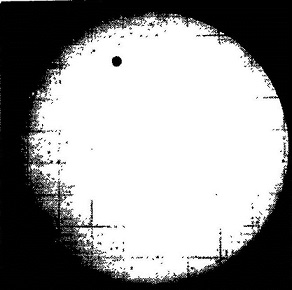 होना पड़ेगा। इसलिए हम एक अन्य खगोलीय पिंड की मदद लेंगे। हम अपनी मापपट्टी के रूप में शुक्र ग्रह का इस्तेमाल करेंगे।
होना पड़ेगा। इसलिए हम एक अन्य खगोलीय पिंड की मदद लेंगे। हम अपनी मापपट्टी के रूप में शुक्र ग्रह का इस्तेमाल करेंगे।
यह एक विशेष वर्ष है। 8 जून 2004 को पृथ्वी, शुक्र और सूर्य एकदम सीधी रेखा में होंगे। इसलिए हम शुक्र को सूर्य के सामने से गुजरते देखेंगे। यह घटना सूर्य ग्रहण जैसी ही है परन्तु अंतर इतना ही है कि सूर्य और पृथ्वी के बीच में चांद नहीं बल्कि शुक्र होगा। चूंकि चांद पृथ्वी के बहुत नज़दीक है इसलिए उसकी छाया काफी बड़ी होती है। और सूर्य को लगने वाला ग्रहण भी बड़ा होता है। जब शुक्र, सूर्य के सामने से गुजरता है तो यह घटना हमें दोनों, यानी सूर्य और शुक्र के तुलनात्मक आकार मापने का बहुत अच्छा मौका प्रदान करती है।
इसलिए 8 जून को आपको शुक्र को सूर्य के सामने से गुजरते देखना होगा और दोनों के तुलनात्मक व्यास मापने होंगे। ऐसा करने के लिए सूर्य की तरफ सीधा देखने का तो सवाल ही नहीं उठता - आपको ऐसी कोशिश बिल्कुल भी नहीं करनी चाहिए। आपको दीवार या फर्श पर सूर्य की छवि प्राप्त करके यह अनुपात निकालना होगा। इसी अंक में एक आसान-सा टेलिस्कोप बनाकर सूर्य का प्रतिबिम्ब प्राप्त करने का तरीका भी बताया गया है।
शुक्र द्वारा सूर्यग्रहण की आखिरी घटना सन् 1882 में देखी गई थी। उस समय के शुक्र-सूर्य ग्रहण का फोटो हम यहां दे रहे हैं, और इस लेख में दिए गए नापों के लिए उसको इस्तेमाल करेंगे। परन्तु इस बार का आंकड़ा तो आपको अपने अवलोकनों और गणनाओं से निकालना होगा।
| पारगमन कब-कब काफी पहले से खगोलविद यह सोचते रहे हैं कि जब बुध और शुक्र ग्रह सूर्य के सामने से गुजरते हैं तो उन्हें सूर्य की चकती पर एक काले बिन्दु के रूप में दिखाई देना चाहिए। 12वीं सदी के एक अरब खगोलविद अलपेट्राजियस ने अपने अवलोकनों में पाया कि बुध कभी भी सूरज के सामने से गुजरते हुए काले बिन्दु के रूप में दिखाई नहीं देता। इसलिए उसने अनुमान लगाया कि बुध ग्रह का अपना प्रकाश का स्रोत है या वह पारभासी है। उस दौर में टेलिस्कोप नहीं थे, स्वाभाविक है कि आंखों से जितना दिखाई दे उसे आधार मानकर अवधारणाएं बनती थीं। बुध का आकार काफी छोटा होने की वजह से उसे खुली आंखों से पारगमन करते यानी सूर्य के सामने से गुजरते हुए देख पाना कठिन था। लेकिन शुक्र आकार में काफी बड़ा था इसलिए इसे पारगमन करते देख पाना संभव था। केपलर ने अपनी गणनाओं के आधार पर बताया कि सन् 1631 में शुक्र ग्रहण की घटना होने वाली है। इसके बाद पारगमन की अगली घटना आठ साल बाद 4 दिसंबर 1639 में हुई जिसे टेलिस्कोप से छवि प्राप्त करके शायद पहली बार देखा गया। बाद में की गई सूक्ष्म गणनाओं से शुक्र पारगमन के बारे में कई बातें मालूम हुईं। जैसे पारगमन कि यह घटना सिर्फ जून और दिसंबर के महीने में ही होती है और दो पारगमन में बारी-बारी (113+8) व 8 साल की अंतराल होता है। बतौर जानकारी यहां पिछले और आगे होने वाले कुछ शुक्र-ग्रहणों का ब्यौरा दे रहे हैं। 5 जून 1761, 3 जून 1 769 8 दिसंबर 1874, 6 दिसंबर 1882 8 जून 2004, 5 जून 2012 11 दिसंबर 2117, 8 दिसंबर 2225 इस साल 8 जून को यह घटना दिन में भारतीय समय के मुताबिक 10:46 से शुरू होगी और शाम 4:50 तक चलेगी। इस समय पृथ्वी पर कोई भी इंसान ऐसा नहीं होगा जिसने यह घटना देखी हो क्योंकि इससे पहले यह 1882 में घटी थी। |
इस फोटो में दिखाए गए सूर्य का व्यास अत्यन्त बारीकी से नापें। इसे D कहेंगे। इसी तरह फोटो में दिख रहे शुक्र ग्रह का व्यास भी उतनी ही बारीकी से नापें। (हां, चित्र में दिख रहा वही काला धब्बा शुक्र है)। इसे हम V कहेंगे। इन दोनों नापों को आपस में भाग देने से आपको लगभग 33 का अनुपात मिलेगा।
यानी कि D/V= 33 ............... (2)
इसका क्या यह मतलब हुआ कि सूर्य का व्यास, शुक्र के व्यास की तुलना में 33 गुना है? आपको याद होगा कि पूर्ण सूर्य ग्रहण के समय चांद सूर्य को पूरा ढक लेता है। उसका अर्थ यह तो नहीं कि सूर्य के चांद का व्यास बराबर है। यानी कि सूर्य और शुक्र के व्यास में सही अनुपात प्राप्त करने के लिए हमें यह पता लगाना होगा कि शुक्र दरअसल कितनी बड़ी छाया बना रहा है, या इस चित्र में कितनी बड़ा दिख रहा है।
परन्तु यह पता लगाने से पहले एक और अवलोकन देख लेते हैं।
शुक्र केवल सुबह और शाम को नज़र आता है और वह कभी भी हमारे सिर के ऊपर तक नहीं पहुंचता। हम देखना चाहते हैं कि शुक्र आकाश में कहां तक ऊपर आता है। इसके लिए आपको शुक्र को हर महीने देखना होगा और तय करना होगा कि उसकी सबसे ऊपर उठने की स्थिति कौन-सी है। हमें रोज कोण मापना होगा और अपने अवलोकन नोट करते रहना है। परन्तु इसके लिए सबसे पहले हमें कोण मापने का यंत्र बनाना होगा।
आइए कोणमापी बनाएं
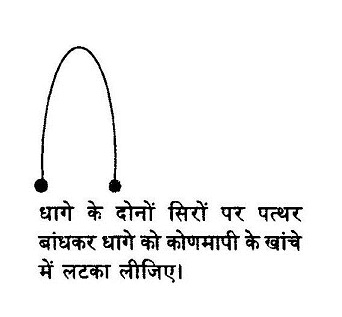
एक गत्ते का टुकड़ा लें। उसके एक किनारे पर बीच में एक खांचा बना लें। धागे के टुकड़े के दोनों छोर पर पत्थर बांध उसे इसे खांचे से चित्र में दिखाए अनुसार लटका दें।
इस गत्ते के टुकड़े को एकदम क्षैतिज पकड़ने पर, इस दोलक का धागा किनारे के एकदम लंबवत होगा। ऐसी स्थिति में धागे की सीध में गत्ते पर एक लंबवत रेखा बना लें। यह हमारी संदर्भ रेखा होगी जिसकी तुलना में हम खगोलीय पिंडों के कोण नापेंगे। किसी भी तारे या ग्रह का कोण नापने के लिए हम इस कोण मापी को चित्र में दिखाए अनुसार उस पिंड की सीध में रखेंगे और धागे की सीध में एक रेखा खींच देंगे। अब गत्ते को जमीन पर रखकर कंपास में मौजूद चांदे के ज़रिए कोण माप लेंगे।
इस तरह हम रोज़ सूर्यास्त के समय शुक्र का कोण नापेंगे। यह कोण सितंबर से मार्च तक हर रोज़ बढ़ेगा और फिर कम होने लगेगा। इस तरह हर रोज़ या हर हफ्ते नाप लेते हुए हम पता कर पाएंगे कि अधिकतम कोण कितना बनता है। मार्च के अंत में यह 47 तक ऊपर उठ जाएगा। यही अधिकतम कोण होगा। अपनी सुविधा के लिए हम इसे 45° मान लेंगे जिससे आगे की गणनाएं आसान हो जाएंगी।
पृथ्वी और शुक्र - सूर्य से कौन कितना दूर 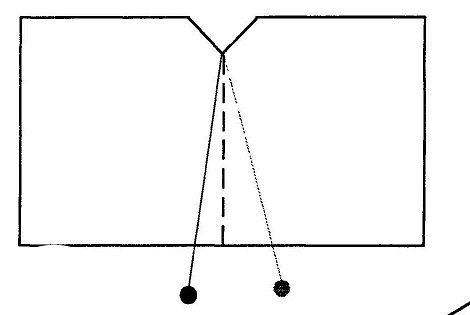
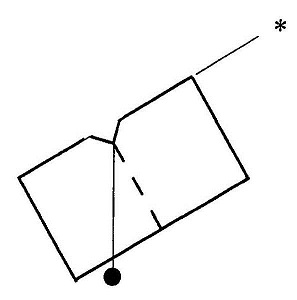 अब हम उस दिन ग्रहों की स्थिति प्रदर्शित करने की कोशिश करते हैं जब शुक्र अधिकतम ऊंचाई पर हो।
अब हम उस दिन ग्रहों की स्थिति प्रदर्शित करने की कोशिश करते हैं जब शुक्र अधिकतम ऊंचाई पर हो।
चूंकि इस दिन पृथ्वी से देखने पर शुक्र अधिकतम कोण बना रहा है, इसलिए कोण S-E1-V1 45° है। और चित्र देखने से स्पष्ट होता है कि इस दिन पृथ्वी-शुक्र को जोड़ती रेखा, शुक्र के कक्ष के टेन्जेंशियल होगी यानी शुक्र के कक्ष की स्पर्श रेखा होगी। अगर यह मान लें कि शुक्र का परिभ्रमण कक्ष वक्राकार है (अंडाकार नहीं जैसा कि हम जानते हैं) तो यह स्पर्श रेखा त्रिज्या से 90° का कोण बनाएगी। एक कोण नब्बे अंश को और दो 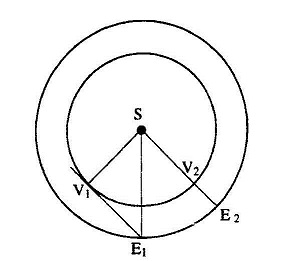
 कोण पैंतालिस अंश के बनने के कारण E1-V1-S समकोण समद्विबाहु (Isosceles) त्रिभुज होगा।
कोण पैंतालिस अंश के बनने के कारण E1-V1-S समकोण समद्विबाहु (Isosceles) त्रिभुज होगा।
यानी कि उस दिन पृथ्वी और शुक्र की दूरी, शुक्र और सूर्य की दूरी के बराबर होगी। और पृथ्वी और सूर्य के बीच की दूरी इन दोनों में से किसी भी एक को 2 गुना होगी (क्योंकि S E, इस समकोण त्रिभुज का कर्ण है)।
यानी कि
पृथ्वी सूर्य दूरी = √2x शुक्र-सूर्य दूरी
पृथ्वी-सूर्य दूरी/शुक्र-सूर्य दूरी =√2......... (3)
शुक्र और शुक्र की छाया
अब हम फिर से 8 जून की स्थिति को देखें। उस दिन शुक्र एकदम पृथ्वी और सूर्य की लाईन में है।
इस चित्र से स्पष्ट है कि त्रिभुज E-V-V1 और त्रिभुज E - S - S1 समरूप त्रिभुज हैं। इसलिए उनकी भुजाओं को अनुपात बराबर होगा।
| शुक्र कभी भी मध्यरात्रि को क्यों नहीं दिखाई देता? शुक्र एक मजेदार ग्रह है (शायद अलग-अलग पहलुओं से देखने पर सभी ग्रह उतने ही मजेदार नज़र आएंगे!)। आपने शायद ध्यान दिया होगा कि शुक्र केवल सुबह-शाम को ही दिखता है - काफी सारे अन्य ग्रहों की तरह साल भर किसी भी दिन मध्यरात्रि को नहीं दिखाई देता। मंगल, गुरू, शनि आदि अक्सर मध्यरात्रि को भी दिखाई दे जाते हैं। क्या आप सोच सकते हैं कि शुक्र के ऐसे व्यवहार का कारण क्या है?  सौर्य मंडल में 9 प्रमुख ग्रह हैं जो सूर्य के इर्द-गिर्द परिक्रमा करते हैं। सूर्य से सबसे नज़दीक बुध है, उसके बाद शुक्र और फिर पृथ्वी की बारी आती है। और आगे बढ़ने पर मंगल... और फिर अंत में प्लूटो। सौर्य मंडल में 9 प्रमुख ग्रह हैं जो सूर्य के इर्द-गिर्द परिक्रमा करते हैं। सूर्य से सबसे नज़दीक बुध है, उसके बाद शुक्र और फिर पृथ्वी की बारी आती है। और आगे बढ़ने पर मंगल... और फिर अंत में प्लूटो।ऊपर दिए गए चित्र को देखें। जब भी पृथ्वी पर खड़ा कोई व्यक्ति शुक्र को देखता है तो शुक्र अपने कक्ष में कहीं भी हो, हमें सूर्य की तरफ ही देखना पड़ता है। चूंकि सूर्य एक तारा है और अत्यन्त चमकीला है, इसलिए जब भी शुक्र दिन के समय सूर्य की दिशा में हो तो वह दिखाई नहीं देता। इसलिए बुध और शुक्र को हम केवल सूर्योदय या सूर्यास्त के समय ही देख सकते हैं। अब मंगल को देखिए, चूंकि हमारी तुलना में वह सूर्य से और दूर है इसलिए हम उसे रात के समय भी देख पाते हैं - पृथ्वी के जब वह बाईं तरफ हो, जैसा कि चित्र में दिखाया गया है। यानी कि जिस तरफ सूर्य है उसके विपरीत दिशा में मंगल हो तो वह रात को भी दिखाई देगा। यह चित्र जून माह में ग्रहों की स्थिति को ध्यान में रखकर नहीं बनाया गया है फिर भी इस चित्र को देखकर बताइए गुरु को रात में देखा जा सकेगा या नहीं? |
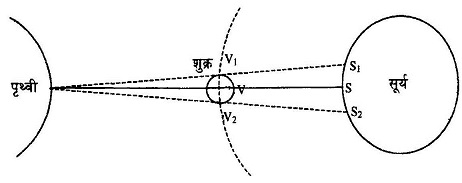 यानी कि
यानी कि
(पृथ्वी-शुक्र की दूरी )/(शुक्र का व्यास) = (पृथ्वी-शुक्र की दूरी )/(शुक्र की छाया का व्यास)
(शुक्र का व्यास)/(शुक्र की छाया का व्यास) = (8 जून को पृथ्वी-शुक्र की दूरी)/(पृथ्वी-सूर्य दूरी)
= ( सूर्य-पृथ्वी दूरी - शुक्र-सूर्य दूरी )/(पृथ्वी-सूर्य की दूरी)
= 1 - ( शुक्र-सूर्य दूरी )/(पृथ्वी-सूर्य की दूरी)
इस समीकरण में समीकरण 3 का अनुपात डालने पर :
(शुक्र का व्यास )/(शुक्र की छाया का व्यास)= 1 - 1/√2 = 0.293
शुक्र की छाया का व्यास = शुक्र का व्यास/0.293
= 3.4 x शुक्र का व्यास ............... (4)
सूर्य के विभिन्न माप
शुक्र-सूर्य ग्रहण के फोटो से हमने समीकरण-2 में पता किया था कि
सूर्य का व्यास/शुक्र की छाया का व्यास = 33
इसमें समीकरण-4 से प्राप्त शुक्र की छाया का व्यास रखने परः
सूर्य का व्यास = 33 x 3.4 x शुक्र का व्यास
= 112 x शुक्र का व्यास
इसलिए
सूर्य का व्यास/शुक्र को व्यास = 112 .............. (5)
अब हमारे पास सूर्य का व्यास शुक्र के रूप में उपलब्ध है और हम जानते हैं कि पृथ्वी से सूर्य की दूरी, सूर्य के व्यास का 110 गुना है।
इसलिएः
पृथ्वी से सूर्य की दूरी = 110 x 1 12 x शुक्र का व्यास
मंज़िल आ ही गई
इस तरह आखिरकार हम जिस दूरी को मापना चाहते थे वो हमारे पैमाने यानी शुक्र ग्रह के व्यास के रूप में प्राप्त हो गई है। अब बच यही जाता है कि इस पैमाने को अंकित (Calibrate) किया जाए। यह भी आसानी से संभव है अगर हम एक अत्यन्त महत्वपूर्ण अनुमान लगाएं। हम मान लेते हैं कि पृथ्वी और शुक्र का आकार लगभग एक जितना है।
यह मान्यता एकदम ठीक नहीं है परन्तु हमारे अन्य अवलोकनों जितनी सटीकता तो इसमें भी है। इसलिए इस मान्यता से भी हमें काफी ठीक-ठीक जवाब मिल जाएगा।
पृथ्वी-सूर्य की दूरी = 110 x 1 12 x पृथ्वी का व्यास .......... (6)
इस तरह हमें यह दूरी खगोलीय पैमाने पर नहीं बल्कि अपनी पृथ्वी पर आधारित पैमाने के रूप में प्राप्त हो गई।
अब या तो पृथ्वी के व्यास के बारे में जो जानकारी हमें मालूम है उसे इस समीकरण में रखकर गणना कर लें - या फिर अभी तक जिस रास्ते आगे बढ़े थे, उसी अंदाज़ में प्रयोग करते हुए यह माप भी खुद निकालें।
| ग्रहण किस्म-किस्म के जब भी ग्रहण की बात होती है तो सबकी जुबान पर सूर्यग्रहण और चंद्रग्रहण का नाम सबसे पहले आता है। लेकिन हमारे आकाश में इन दो के अलावा और भी ग्रहण लगते हैं मसलन शुक्र, बुध का सूर्य की चकती के आगे से गुजरना। इसी तरह बृहस्पति, शनि, यूरेनस, नेपच्यून के काफी सारे उपग्रह हैं इसलिए वहां तो ग्रहण की ढेरों संभावनाएं हैं। जैसे मंगल की ही बात करें तो इसके दो उपग्रह हैं – फोबोस और डिमोस। यदि आप मंगल के 0° अक्षांश यानी कि मंगल -मध्य रेखा पर खड़े हैं तो आप इन दोनों उपग्रहों को सूर्य की चकती के सामने से गुजरता हुआ देख सकते हैं। एक मंगल वर्ष (689 दिन) में फोबोस को 1300 बार ट्रांजिट करते देखा जा सकता है, और हर बार उसे सूर्य की चकती के सामने से गुजरने में लगेगा तकरीबन 19 सेकेंड का समय। डिमोस एक मंगल वर्ष में 130 बार ट्रांजिट करता दिखाई देता है। हर बार ट्रांजिट में लगने वाला समय होता है तकरीबन 1 मिनट और 48 सेकेंड। अभी तो हमने सिर्फ मंगल की ही बात की है, जिन ग्रहों के पास ढेरों उपग्रह हैं, वहां ग्रहणों की बात सोचकर ही रीढ़ की हड्डी में सिहरन होने लगती है। अब जब आप मंगल पर खड़े ही हैं तो एक और रोचक जानकारी देना चाहेंगे - यदि आप मंगल पर सन् 2084 की नवंबर तक बने रहते हैं तो आप एक और नज़ारा देख सकेंगे। और वह नज़ारा है ट्रांजिट ऑफ अर्थ। यानी मंगल पर खड़े होकर आप पृथ्वी को सूर्य की चकती के सामने से गुजरते हुए देख पाएंगे। मंगल से ट्रांज़िट ऑफ अर्थ देख पाने के मौके कम ही मिलते हैं। पिछली सदी में मई 1905 और मई 1984 को ऐसे मौके आए थे। 1984 में मंगल से देखते हुए पृथ्वी को सूरज की चकती पार करने में साढ़े आठ घंटे का समय लगा था। अब अगला अवसर नवंबर 2084 और नवंबर 2163 में मिलेगा। एक और किस्म का ग्रहण है जिसकी ओर हमारा ध्यान कम ही जाता है। कभी-कभार अखबारों में खबर छपे तो ही पता चल पाता है कि कोई तारा या ग्रह कुछ देर के लिए चांद के पीछे छुप रहा है। इसी तरह बुध, शुक्र, बृहस्पति के पीछे भी कई बार कुछ तारे छिप जाते हैं। इस घटना को Occultation कहते हैं। यदि आपको याद हो तो डेढ़-दो साल पहले शनि ग्रह चांद के पीछे छुप गया था। इस घटना को भारत में भी देखा गया था। |
पृथ्वी का व्यास
पृथ्वी का व्यास पता करने के कई तरीके हैं। उनमें से हम यहां एक ऐसे तरीके का जिक्र कर रहे हैं जो स्कूल में पढ़ने वाला कोई भी विद्यार्थी अपना सकता है। परन्तु दुर्भाग्यवश यह तरीका केवल वहीं इस्तेमाल किया जा सकता है जहां पर सूर्य को समंदर में अस्त होता देखा जा सके - यानी कि भारत के पश्चिम समुद्री तट पर कहीं भी यह तरीका अपनाया जा सकता है।
आपको पश्चिमी समुद्री तट के पास कोई ऊंची इमारत ढूंढनी होगी। इस प्रयोग के लिए आपको अपने एक दोस्त की भी जरूरत होगी। आपका दोस्त ज़मीन पर खड़ा रहेगा और आप इमारत के ऊपर, जहां से आप पश्चिमी क्षितिज और अपने दोस्त दोनों को देख पाएं। किसी ऐसी शाम जब आकाश पर बादल न हों, आप यह प्रयोग कर सकते हैं। जब सूर्य अस्त हो रहा हो तो आपको दोस्त अपना हाथ ऊपर किए खड़ा रहेगा। जिस क्षण उसे दिखे कि सूर्य का अंतिम छोर समुद्र में अस्त हो गया है, वो अपना हाथ नीचे कर देगा। यह इशारा मिलते ही आप समय की गिनती करना शुरू कर देंगे - उसी पत्थर और धागे से बने दोलक का दोलन शुरू करके या स्टॉप वॉच चालू करके। इमारत के ऊपर खड़े होने की वजह से आपको अभी भी सूर्य दिखाई देगा। समय की गिनती तब तक जारी रखें जब तक कि आपके लिए भी सूर्य पूरी तरह डूब न जाए। आइए इस समयांतर को T सेकंड कहें।
अब दूसरा काम है उस इमारत की ऊंचाई नापना, जिस पर चढ़कर आपने प्रयोग किया। यह पता करने के भी बहुत सारे आसान तरीके हैं। आप इमारत की छाया के आधार पर अंदाजा लगा सकते हैं, या फिर इमारत से इतनी दूरी पर पहुंच जाएं जहां से इमारत का ऊपरी हिस्सा 45° का कोण बनाता दिखाई दे। स्वाभाविक है कि आपको यह कोण कोण-मापी के जरिए मापना होगा। और फिर बस आप जहां खड़े हैं वहां से इमारत तक की दूरी माप लें। यही उस इमारत की ऊंचाई है। आइए, इसे ऊंचाई को H कहें।
अब आगे दिया हुआ चित्र देखें। इसमें R पृथ्वी की त्रिज्या है और H इमारत की ऊंचाई है। X वह दूरी है जहां तक आप इमारत के ऊपर से देख सकते हैं।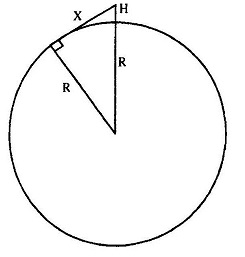
X2 + R2 = (R+H)2
= R2 + 2RH + H22
X2 = 2RH + H2
हम H’ को नजरअंदाज़ कर सकते हैं क्योंकि 2RH की तुलना में यह नगण्य है।
इसलिए X2 = 2RH
X= 2RH
चूंकि X वह दूरी है जहां तक आप इमारत के ऊपर से देख सकते हैं, इसलिए आप जो कुछ अतिरिक्त समय सूर्य को देख पाए - पृथ्वी को X दूरी घूमने के लिए लगा समय है वह।
हम जानते हैं कि पृथ्वी को अपनी धुरी के इर्द-गिर्द एक चक्कर लगाने में 24 घंटे लगते हैं, यानी 86,400 सेकंड। यानी कि T सेकंड में पृथ्वी अपनी परिधि का 1/86,400 गुना घूम गई होगी।
यानी X = T x पृथ्वी की परिधि 86,400
= T x 2R /86,400 ............. (7)
पायथोगोरस के नियम का इस्तेमाल करते हुए हमने ऊपर के चित्र में देखा था कि
X= 2 RH ............... (8)
समीकरण 7 और 8 की तुलना करने पर
X= Tx 2 T R/86,400 = V2RH
RNR = (86,400/T) x (2H/27)
VR = (86,400/T) x (H/27)
R= (86,400/T) x H/2n............... (9)
अब फिर से समीकरण 6 को याद करते हैं - यानी हमारे असली सवाल का हलः
सूर्य और पृथ्वी के बीच की दूरी = 110 x 112 x 2 x R .... (10)
ऊपर दिए गए इन दोनों समीकरणों में वे सब हिस्से हैं जिनके नाप हमने पता किए हैं - और जिनके आधार पर हम सूर्य और पृथ्वी के बीच की दूरी का पता लगा सकते हैं।
तो अंत में हमने अपनी मंज़िल हासिल कर ही ली। खगोलीय दूरियां मापने की तरफ पहला कदम है यह। चाहे इस लेख ने इसे आपके लिए काफी आसान बना दिया - फिर भी यह कोई छोटा कदम नहीं है। इस लेख के जरिए हमने केवल रुचि पैदा करने की कोशिश ही नहीं की है बल्कि ऐसी और बहुत सारी गणनाएं करने के लिए एक आधार तैयार किया है ताकि आप ब्रह्मांड का आकार-साइज़ नापने की तरफ कदम बढ़ा पाएं!!
परन्तु यह लेख अभी भी पूरा नहीं हुआ है, क्योंकि मैंने उस दूरी का कोई आंकड़ा तो दिया ही नहीं जिसे नापने हम निकले थे। ऐसा इसलिए क्योंकि अभी आपको प्रयोग करना है और अपना परिणाम प्राप्त करना है। प्रयोग करने पर आप पृथ्वी-सूर्य की दूरी का जो आंकड़ा प्राप्त करें - वो हमें ज़रूर लिखें।
आमोद कारखानिस: कम्प्यूटर वैज्ञानिक, चित्रकार व प्रकृति प्रेमी। मुंबई में रहते हैं।
विवेक मोन्टेरोः मूलतः भौतिकशास्त्री। वामपंथी मज़दूर संगठनों के दलों में सक्रिय। नवनिर्मिती, मुंबई के संचालक।
इस विषय पर और जानकारी प्राप्त करने के लिए देखें:
www.navnirmiti.org/tov
|
पिनहोल के जरिए सूर्य का प्रतिबिम्ब कुछ अवलोकन, कुछ व्याख्या |
सामान्य पंच से भी सुराख बना सकते हैं। अब इस कागज़ को दर्पण के सामने लगभग 30 से.मी. की दूरी पर इस तरह से रखें ताकि कागज/कार्डशीट दर्पण से परावर्तित प्रकाश को अवरुद्ध करे। कागज़ को प्रकाश किरणों के एकदम लंबवत रखें। अब कमरे के अंदर दीवार पर बन रही छवि को देखें।
है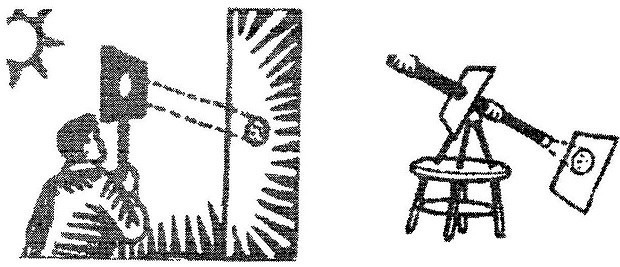 रानी की बात है कि छवि का साइज़ छोटा नहीं होता जबकि अब हमने दर्पण की तुलना में एक बहुत छोटा सुराख बनाया है। छवि की तीव्रता ज़रूर कम हो जाएगी, परन्तु अब वह ज्यादा स्पष्ट दिखेगी। दीवार पर जहां पर प्रतिबिम्ब बन रहा है वहां आप एक सफेद कागज चिपका सकते हैं ताकि छवि और भी बेहतर हो और आप बारीकी से माप ले सकें।
रानी की बात है कि छवि का साइज़ छोटा नहीं होता जबकि अब हमने दर्पण की तुलना में एक बहुत छोटा सुराख बनाया है। छवि की तीव्रता ज़रूर कम हो जाएगी, परन्तु अब वह ज्यादा स्पष्ट दिखेगी। दीवार पर जहां पर प्रतिबिम्ब बन रहा है वहां आप एक सफेद कागज चिपका सकते हैं ताकि छवि और भी बेहतर हो और आप बारीकी से माप ले सकें।
इस तरीके से आपको प्राप्त होने वाली छवि का व्यास लगभग 30 से.मी. होगा। 8 जून 2004 को जब शुक्र, सूर्य के सामने से गुजरेगा तो आपको शुक्र की छाया लगभग एक से.मी. व्यास की काली चकती के रूप में दिखेगी।
दो और तरीके हैं सूर्य की और बेहतर छवि आसानी से प्राप्त करने के। चार से छ: मीटर लंबी फोकल दूरी का एक उत्तल लेंस इस्तेमाल करेक चित्र में दिखाए अनुसार उससे दीवार पर सूर्य की छवि प्राप्त कर सकते हैं।
इसी तरह साधारण टेलिस्कोप से कागज़ या पर्दे पर छवि प्राप्त की जा सकती है। इसके लिए टेलिस्कोप का आगे वाला लेंस लगभग 1 मीटर फोकल दूरी का हो और पीछे वाला आई-पीस 5 सेमी फोकल दूरी का हो तो अच्छा परिणाम मिलेगा।



 हमने नीचे दिए कुछ प्रयोग किए।
हमने नीचे दिए कुछ प्रयोग किए। 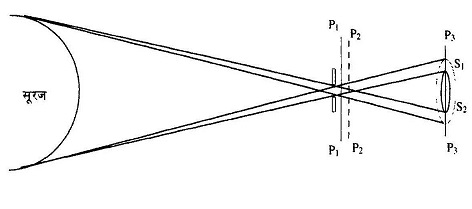 प्रयोग को आगे बढ़ाते हमने यह भी पाया कि
प्रयोग को आगे बढ़ाते हमने यह भी पाया कि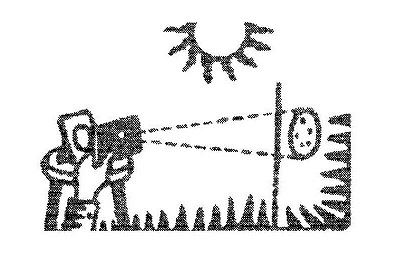 यह प्रयोग ऐसे किसी भी कमरे में किया जा सकता है जिसका कोई दरवाज़ा या खिड़की बाहर खुलता हो। यह भी देख लीजिए कि खिड़की-दरवाज़े पर पर्दा डालकर इस कमरे को पर्याप्त अंधेरा किया जा सकता है। घुप्प अंधेरे की ज़रूरत नहीं है, प्रयोग करते वक्त आप खुद तय कर पाएंगे कि कितना अंधेरा पर्याप्त होगा।
यह प्रयोग ऐसे किसी भी कमरे में किया जा सकता है जिसका कोई दरवाज़ा या खिड़की बाहर खुलता हो। यह भी देख लीजिए कि खिड़की-दरवाज़े पर पर्दा डालकर इस कमरे को पर्याप्त अंधेरा किया जा सकता है। घुप्प अंधेरे की ज़रूरत नहीं है, प्रयोग करते वक्त आप खुद तय कर पाएंगे कि कितना अंधेरा पर्याप्त होगा।