इतिहास: किस काम का है यह?

पुस्तक अंश

शेषािगरी केएम राव

“मुझे यकीन है कि किसी विषय को उसके इतिहास से जुदा करने पर उतना नुकसान नहीं होगा, जितना गणित में।”
- ग्लैशियर

नौवीं के छात्रों की एक कक्षा की कल्पना कीजिए जो ‘लॉगरिद्म’ (लघुगणक) सीखने वाले हैं। एक ऐसे शिक्षक की कल्पना कीजिए जो कक्षा में घुसते ही घोषणा कर देता है: “आज हम लॉगरिद्म के बारे में सीखेंगे।” सामने उपस्थित भावशून्य चेहरों को देखकर थोड़ा अनिश्चित ढंग से वह ब्लैकबोर्ड की ओर मुड़ता है और लिखने लगता है, शायद उतने ही ढुलमुल यकीन से:
यदि ax = y हो, तो x को आधार a पर y का लॉगरिद्म कहते हैं जिसे निम्नानुसार लिखा जाता है x = logay. तो यदि 23 = 8 है, तो 3 को 2 के आधार पर 8 का लॉगरिद्म कहा जाता है, जिसे इस तरह लिखा जाता है log28 = 3.

इसके बाद शिक्षक मुड़कर आपसे मुखातिब होता है। यदि आप इस शिक्षक की कक्षा में छात्र होते तो कैसा लगता? यदि ‘लॉगरिद्म’ नाम के इस जीव के बारे में आप कुछ नहीं जानते तो फिलहाल इस बात की चिन्ता न करें। उस पर बाद में आएँगे। दरअसल, लॉगरिद्म एक विलक्षण विचार है, बशर्ते कि उसे ठीक से समझाया जाए। अन्यथा यह एक दु:स्वप्न साबित हो सकता है।
मैं देख सकता हूँ कि लाचारी उभरने लगी है। सही कहें तो सारे शिक्षक लॉगरिद्म की कक्षा इस तरह से शुरू नहीं करेंगे। ज़्यादा सम्भावना इस बात की है कि वे छात्रों सेे कुछ सवाल आमंत्रित करेंगे। यदि कोई छात्र पूछता है कि लॉगरिद्म होता क्या है और इनकी ज़रूरत क्या है, तो शिक्षक शायद कहें कि इनकी ज़रूरत जटिल गणितीय गणनाओं को सरल बनाने में पड़ती है। यदि शिक्षक ने जॉन नेपियर के बारे में पढ़ा-सुना है तो वे बता सकती हैं कि लॉगरिद्म की खोज किसने की थी। हो सकता है कि वे कुछ ‘बुनियादी’ (मगर विचित्र) सूत्र प्रस्तुत कर दे, जैसे
 (logxab = logxa + logxb )
और (logxa/b = logxa - logxb)

उम्मीद करता हूँ कि आप अभी तक मौजूद हैं। एक बार फिर, यह चिन्ता मत कीजिए, कम-से-कम अभी तो न कीजिए, कि इन सूत्रों का मतलब क्या है।
जल्दी ही आप देखेंगे कि ये छात्र अध्याय के अन्त में दिए गए सवालों की ओर बढ़ रहे हैं। हम शर्त लगा सकते हैं कि वे भी यही पूछ रहे होंगे, “ये सब है क्या? हमें यह सब क्यों चाहिए? यह रायता किसने फैलाया है?”
इनमें से हरेक सवाल की एक रोचक कहानी है, जो कक्षा में जान फूँक सकती है। शिक्षकों को प्रोत्साहित किया जाना चाहिए कि वे ऐसी कहानियाँ हासिल करें जो जिज्ञासा को पनपाएँ और सीखने को मज़ेदार बनाएँ। यदि इस तरह का उत्साह पैदा न किया जाए, तो गणित की कक्षाएँ नीरस साबित हो सकती हैं। तब हम सिखाए जा रहे गणित में सन्दर्भ और अर्थ जोड़ने का महत्वपूर्ण अवसर गँवा देते हैं।

लीलावती की रचना
मैं लॉगरिद्म की कहानी थोड़ी देर में सुनाऊँगा। मैं यकीन दिलाता हूँ कि वह कहानी इलहाम (रहस्योद्घाटन) से कम नहीं होगी। फिलहाल में वे कहानियाँ साझा करूँगा जो हमने चन्ना से सुनी थीं। हमें यह देखना होगा कि हमारे लिए उनका अर्थ क्या है। पर वह काम कहानी सुनने के बाद करते हैं।
चन्ना के साथ अपने दूसरे वर्ष में, जब हम द्विघात समीकरणें सुलझाना सीख रहे थे, उन्होंने भारतीय गणितज्ञ भास्कराचार्य द्वितीय और उनकी पुत्री लीलावती की कहानी सुनाई थी। चन्ना ने यह कहानी भास्कर के ग्रन्थ लीलावती के अनुवाद में से उठाई थी। यह पुस्तक उन्हें उनके मित्र वेंकटरमन ने कर्नाटक के शिमोगा ज़िले के एक सुन्दर गाँव मत्तूर की गलियों में बचपन में दी थी।
हमने चन्ना से बेचारी लीलावती के बारे सुना जिसके बारे में ज्योतिषियों ने भविष्यवाणी की थी कि उसका विवाह कभी नहीं होगा। लेकिन भास्कर, जो स्वयं एक ज्योतिषी थे, गणना करके वह तारीख और समय निर्धारित नहीं कर पा रहे थे जब वह विवाह कर सकेगी। यदि वह समय टल गया तो लीलावती की शादी का मामला ही खत्म हो जाएगा। तब गणितज्ञ भास्कर ने एक घड़ी बनाई जिसमें लोटे में पानी भरते-भरते वह ठीक उस समय डूब जाएगा जब लीलावती विवाह कर सकती है। लेकिन उत्साह और बेसब्री के चलते लीलावती उस घड़ी पर झुक गई और उसे ध्यान ही न रहा कि उसकी माला का एक मोती गिर गया था और उस मोती ने वह छेद बन्द कर दिया जिसमें से पानी धीरे-धीरे जल-घड़ी में भर रहा था।

नतीजा यह हुआ कि मुहूर्त का सही-सही निर्धारण न हो पाया क्योंकि जल-घड़ी की व्यवस्था तो अस्त-व्यस्त हो गई थी। लीलावती नाखुश और लाचार रह गई। अन्तत: उसका विवाह हुआ ज़रूर किन्तु उसके पति की मृत्यु जल्दी ही हो गई। उसके पति की असमय मृत्यु का दोष विवाह के अशुभ समय पर मढ़ा गया। अपनी उदास पुत्री को तसल्ली देने के लिए भास्कर ने लीलावती (गणितीय ग्रन्थ) की रचना की। यह 1150 ईस्वी के आसपास की बात है। उनका विश्वास था कि इस तरह लीलावती का नाम अमर हो जाएगा। वह उद्देश्य तो निसन्देह पूरा हुआ।

गणित में काव्य
इस कहानी ने मेरा मन भी बहलाया और उलझाया भी। गणित में इतना कुछ हो रहा था, बेजान द्विघात समीकरण से बहुत अधिक। मैं दक्षिण भारत में कहीं, 1150 ईस्वी में इस महान गणितज्ञ और उसकी पुत्री के बारे में कल्पना करने लगा। वह ज़माना कैसा रहा होगा? उस समय तक तो मैं यह भी नहीं जानता था कि भारत में ऐसे गणितज्ञ थे जो ऐसे सवालों पर काम करते थे। हम सोचते थे कि इतिहास में सारे गणितज्ञ यूरोप या उसके आसपास ही होते थे। हममें से कई लोग आज भी यही सोचते हैं, और भूल जाते हैं कि भारत में कई हज़ार वर्षों पहले गणितीय सोच की एक समृद्ध परम्परा थी। मेरे लिए तो यही एक बड़ा सबक था, यह  बोध जो सिर्फ चन्ना की गणित की कक्षा में मिला था। इतिहास के पीरियड में तो हम यह मानकर आगे बढ़ जाते कि यह एक और जानकारी है जिसे रट लेना है।

मैं धीरे-धीरे इस दिवास्वप्न में से निकला, तो देखा कि चन्ना साफ-सुथरे अक्षरों में बोर्ड पर निम्नलिखित सवाल लिख रहे हैं:
“चक्र और कौंच पक्षियों से घिरी एक झील में कमल के फूल के डण्ठल की लम्बाई का एक इकाई भाग पानी की सतह के ऊपर दिख रहा है। हल्की हवा से डोलते हुए उसकी नोक उसकी मूल स्थिति से तीन इकाई दूर पानी में डूब जाती है। फटाफट पानी की गहराई बताओ।”

यह बहुत ढीला-ढाला अनुवाद है। मूल संस्कृत में यह इस तरह है:
चक्र क्रौंचाकुलित सलिले क्वापि दृष्टं तडागे
तोयादूर्ध्वं कमल-कलिकाग्रं वितस्तिप्रमाणं।
मन्दं मन्दं चलितमनिलेनाहतं हस्तयुग्मे
तस्मिन्मग्नं गणक कथय क्षिप्रमम्भ:प्रमाणं।।

लीलावती का यह सवाल चन्ना के पसन्दीदा सवालों में से था। वे हर साल छात्रों को यह सवाल दिया करते थे। ज़बानतोड़ू है, नहीं? हममें से जो लोग संस्कृत नहीं जानते, उन्हें तो यह ऊटपटांग ही लगता है। लेकिन उस ज़माने के भारतीय गणितज्ञ इसी भाषा का उपयोग करते थे। भास्कर जैसे गणितज्ञ उच्च कोटि के कवि भी थे जो अपने गणित की रचना काव्य में किया करते थे। सौन्दर्यबोध उनके काम का अभिन्न अंग था। लीलावती का सवाल भी सुन्दरता से रचा गया है और चन्ना ने इसे यथासम्भव कुशलतापूर्वक बोर्ड पर चित्रित किया ताकि हम इसका विश्लेषण कर सकें।
मान लीजिए हम कहते हैं कि कमल के डण्ठल के जलमग्न हिस्से की लम्बाई ‘x’ है, तो कुल लम्बाई ‘x+1’ इकाई होगी। जो लम्बाई जलमग्न है वह उस जगह पर झील की गहराई की द्योतक है जहाँ कमल खड़ा है। यदि हम मानें कि कमल एकदम सीधा खड़ा है, तो इसका मतलब होगा कि कमल का डण्ठल पानी की सतह के साथ समकोण बनाता है। हम यह भी मान रहे हैं कि कमल झील के पेन्दे में से निकला है। (कमल के पौधे वास्तव में तैरते हैं, लेकिन भास्कर को इस बात के लिए क्षमा किया जा सकता है, यह कोई बहुत बड़ी गलती नहीं है।)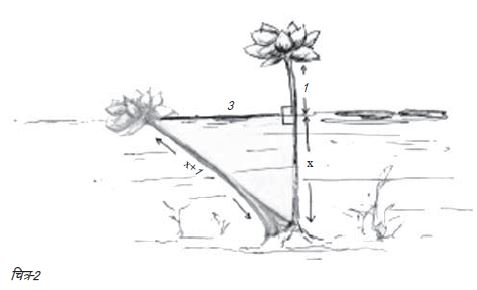

इस सवाल में (x+1) डण्ठल की वह लम्बाई है जो हवा से डोलते हुए अपने मूल स्थान से तीन इकाई दूर जाकर पानी में टिक जाती है। जैसा कि हमारे चित्र से स्पष्ट है, हमारे पास एक त्रिभुज है जिसकी भुजाएँ 3 इकाई, x इकाई और (x+1) इकाई हैं। (x+1) विकर्ण का द्योतक है (वह पूरा डण्ठल जो अब जलमग्न है), जबकि 3 व x अन्य दो भुजाएँ हैं। पायथागोरस प्रमेय को लागू करने पर हमें निम्नलिखित मिलता है:
(विकर्ण)2 = अन्य दो भुजाओं के वर्गों का योग
(x+1)2 = x2 + 32
बाईं बाजू को विस्तारित करके समीकरण को हल करने पर हमें मिलता है:
x2 + 2x + 1 = x2 + 32
2x + 1 = 9
2x = 8

लिहाज़ा,  x = 4 इकाई, जो उस जगह पर झील की गहराई है जहाँ कमल पेन्दे में खड़ा है। “देखो!” भास्कर ने ठीक उसी तरह कहा होगा जैसे चन्ना की युक्लिडियन आदत है ‘QED’ कहने की।
इस समीकरण के बारे में एक बात और कहना मुनासिब होगा। यह शुरू तो एक द्विघात समीकरण के रूप में होती है (क्योंकि इसमें x की सबसे बड़ी घात 2 है यानी x2 में) लेकिन इसका हल एक सरल समीकरण के रूप में होता है क्योंकि दोनों तरफ x2 कट जाते हैं। लीलावती के कई सवालों की प्रकृति द्विधाती है। इस सवाल के समान उनमें x2 कटते नहीं हैं बल्कि उन्हें एक विधि से हल करना पड़ता है जिसे गुणनखण्डन (factorisation) कहते हैं। छात्र इसे हाई स्कूल में सीखते हैं। आपकी भूख जगाने के मकसद से मैंने पुस्तक के अन्त में कल्पनाशील ढंग से बनाया गया एक सवाल जोड़ा है।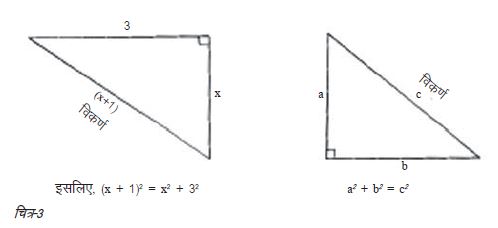

यदि आप जाना-पहचाना पायथा-गोरस प्रमेय भूल गए हों, तो मैं एक समकोण त्रिभुज के चित्र (चित्र-3) की मदद से आपकी याद ताज़ा कर देता हूँ। लीलावती के सवाल की तुलना हम किसी भी समकोण त्रिभुज से कर सकते हैं।
अब द्विघाती समीकरण कोई रूखा सूत्र या प्रक्रिया नहीं रह गई थी। हमें यह सवाल हल करने में मज़ा आया था और कक्षा जीवन्त हो उठी थी। मेरे लिए इसका लुभावना हिस्सा अतीत में चहलकदमी का था। मुझे लग रहा था जैसे मैं तकरीबन 900 साल बाद भास्कराचार्य से वार्तालाप कर रहा हूँ। यह भी एक बड़ा बोध हुआ था कि भारत में महान गणितज्ञ हुए हैं - हज़ारों वर्ष पहले - जिन्होंने उन चीज़ों पर काम किया था जिन्हें हम 1984 में स्कूल में पढ़ रहे थे।
आखिर में, एक अन्यथा उबाऊ कवायद रोमांचक साबित हुई क्योंकि हमने द्विधाती समीकरण की ऐतिहासिक कड़ियों के साथ-साथ उनके व्यावहारिक महत्व को भी देखा। वास्तव में, चमत्कार तो कहानी ने किया था, ठीक उसी तरह जैसे युक्लिड और प्रमाणों को लेकर उनके दृष्टिकोण की कहानी ने किया था, हालाँकि युक्लिड का मामला तो इतिहास में और भी पीछे जाता है, और भी ज़्यादा पेचीदा है। हमारा सम्पर्क गणित के रोमांचक विषयों से होने लगा था। मैं सोचने लगा, “गणित का इतिहास कितना पुराना है?”

इससे पहले कि हम गणित शिक्षण में ऐतिहासिक पद्धति के उपयोग की और चर्चा करें, जुगाली के लिए भास्कराचार्य का एक और सवाल हाज़िर है। इसमें एक द्विघाती समीकरण प्राप्त होती है जिसको हल करने के लिए गुणनखण्ड का सहारा लेना पड़ता है:
“मधुमक्खियों के एक झुण्ड में से, मधुमक्खियों की कुल संख्या के आधे के वर्गमूल के बराबर संख्या में मधुमक्खियाँ उड़कर कमल के फूल पर पहुँचीं। जल्दी ही, झुण्ड का 8/9 भाग उड़कर उसी कमल के फूल पर पहुँचा। कमल की सुगन्ध से मोहित होकर एक नर मधुमक्खी एक फूल में घुस गई। लेकिन जब वह अन्दर थी, तभी रात हो गई और फूल बन्द हो गया। मधुमक्खी अन्दर कैद हो गई। उसकी भिनभिनाहट सुनकर उसकी साथी बाहर से चीखी, ‘ओ मेरे प्यारे'। झुण्ड में कितनी मधुमक्खियाँ थीं?”
जितना इसके बारे में सोचता हूँ, मुझे लगता है कि चन्ना एक श्रेष्ठ इतिहास शिक्षक और किस्सागो थे। हमारे नियमित इतिहास शिक्षक से तो वे निश्चित रूप से बेहतर थे जो कक्षा में बढ़ते कोलाहल के बीच सिर झुकाकर पाठ्यपुस्तक में से वाचन करके इतिहास का गला घोंटा करते थे। कभी-कभी तो हम सो जाते थे। यह समय की बरबादी के अलावा कुछ नहीं था। अलबत्ता, कभी-कभी मज़ा भी आता था, हालाँकि उनका ऐसा कोई इरादा नहीं होता था। शिक्षक की बेखबरी में हम कागज़ के हवाई जहाज़ और रॉकेट, चॉक के टुकड़े वगैरह फेंकते रहते थे जबकि वे विषयवस्तु के उबाऊ वाचन में व्यस्त रहते। मुझे याद नहीं पड़ता कि कभी उन्होंने सिर उठाकर देखा हो और हमें डाँटा हो।

छात्रों की गणित में अरुचि
चन्ना वास्तव में इतिहास का उपयोग कैसे करते थे? इसका जवाब देने से पहले हमें एक अन्य बुनियादी सवाल पूछना होगा: छात्रों को गणित मुश्किल और अरुचिकर क्यों लगता है? इस सवाल के कई जवाब हो सकते हैं, जैसे खराब शिक्षण, शिक्षक की अपर्याप्त तैयारी वगैरह।
चन्ना द्वारा पढ़ाए जाने के अपने अनुभव के आधार पर मेरा जवाब है कि हमारे पास ऐसे शिक्षक नहीं हैं जो गणित के रहस्यों की पर्याप्त पड़ताल करते हों। यदि ऐसा होता है, तो वे ऐसे सवाल पूछने लगते हैं: क्यों? कौन? कहाँ? कैसे? वे विषय के इतिहास में चले जाते हैं। वे कहानियाँ और पैटर्न्स ढूँढ़ने लगते हैं। वे एक बार फिर से विषय के छात्र बन जाते हैं।
लेकिन शिक्षकों को गणित की छानबीन करने को प्रशिक्षत करना एक चुनौतीपूर्ण काम है। चुनौती की शुरुआत तो स्वयं प्रशिक्षकों से होती है। क्या वे जिज्ञासु हैं? क्या वे पढ़ते हैं, मनन करते हैं और सवाल पूछते हैं? वे जो कुछ कर रहे हैं, क्या उसमें उनकी रुचि है, क्या वे अपने विषय को गहराई में टटोलने में रुचि रखते हैं? यही वजह है कि हम अपरिहार्य रूप से उस चीज़ में फँस जाते हैं, जिसे शिक्षाविद शिक्षा की ‘तंत्रगत’ समस्या कहते हैं।

जैसा कि कई सारे सोचने-विचारने वाले पालकों और शिक्षकों ने पहचाना है, शिक्षा की शान्त चुनौती यह है कि अर्थ और समझ के लिए पढ़ाया जाए, इस तरह पढ़ाया जाए कि बच्चे यह समझ सकें कि ‘क्यों’ पढ़ाया जा रहा है। यह चुनौती तब और भी गम्भीर हो जाती है जब गणित पढ़ाने की बात आती है। क्या हम सूत्र और विधियाँ मासूम छात्रों में ठूँसने की बजाय ‘क्यों’ समझाना सीख सकते हैं? सूत्र और विधियाँ ठूृँसते जाना ही वह समस्या है जिसकी वजह से उन्हें गणित का कोई अर्थ समझ नहीं आता और वे उससे दूर हट जाते हैं।
बच्चे तो सदा सवाल पूछते रहते हैं। उनकी जिज्ञासा अन्तहीन होती है। बचपन में हम सब ऐसे ही थे। तो बड़े होकर हमें क्या हुआ? शायद हमें अपने अन्दर के बच्चे को फिर से खोजना होगा। ऐसा करके शायद हम बच्चों के सवालों के जवाब बेहतर ढंग से दे पाएँगे।

जो जिज्ञासा हम वयस्कों के रूप में महसूस नहीं करते, बच्चों में उसे सन्तुष्ट कैसे करें? शायद हमें उन्हें कहानियाँ सुनानी चाहिए। कहानियाँ - जो गणित हम स्कूल में सीखते हैं उसे रचने वाले लोगों की कहानियाँ, हज़ारों साल पहले गणित के विकास की कहानियाँ - कभी रोमांचित करने से नहीं चूकतीं। ये कहानियाँ गणित शिक्षण का अभिन्न अंग बन जानी चाहिए। तभी बच्चे गणित की सच्ची प्रकृति को खोज पाएँगे और इस विषय के प्रति आकर्षण विकसित कर पाएँगे। जब वे गणित को खोजने और रचने का अनुभव कर पाएँगे, तभी वे यह समझ पाएँगे कि यह विषय मात्र सूत्रों और प्रमेयों की कलाबाज़ी से बढ़कर कुछ है।
चन्ना की कार्यशैली में गणित कोई ऐसी चीज़ नहीं थी जो पकी-पकाई आसमान से टपकी हो, जिसका जादुई उपयोग करके आप परीक्षाओं में बढ़िया अंक प्राप्त करें। उनकी नज़र में यह विषय मानवीय पहलू से जुदा और ‘क्यों’ की व्याख्या से रहित अलग-थलग विषय नहीं था।

इतिहास और कहानियों के ज़रिए
शिक्षक के तौर पर अपनी यात्रा में, चन्ना ऐतिहासिक तत्व को शामिल करते थे ताकि हमारी जिज्ञासा को हवा दे सकें और विषय को ज़्यादा मानवीय बना सकें। जब हमने उनके साथ हाई स्कूल की यात्रा की, गणितीय रुझान के साथ या उसके बगैर, तो उन्होंने हमें कई लुभावनी कहानियों की दावत दी। यह उनके शिक्षण की एक प्रमुख तकनीक थी। शायद यह एक सबसे कारगर तरीका है जो सीखने वालों की कल्पना को उड़ान दे सकता है।
गणितीय खोजों की हज़ारों वर्ष पुरानी ऐसी कुछ कहानियों की जड़ें रोज़मर्रा की समस्याओं में थीं। ये कहानियाँ हमें बताती थीं कि गणितज्ञ जादूगर नहीं, बल्कि हमारे जैसे इन्सान होते हैं जिनकी रुचि जीवन में होती है। यह एक बात थी जिसे रटन्त विद्या और गणित-भीती ने हमसे छिपाए रखा था, जब तक कि चन्ना, विषय में अपनी नैसर्गिक रुचि के चलते, हमें खोज-यात्रा पर नहीं ले गए। विषय का इतिहास उनकी उंगलियों पर था और वे जानते थे कि गणित की दुनिया में क्या चल रहा है। जब मात्र परीक्षाएँ उत्तीर्ण करने की बजाय हम अर्थ और समझ की चाह करने लगे, तो हम ज़्यादा-से-ज़्यादा क्यों भी पूछने लगे।

चन्ना का ‘अन्तरविषयी’ तरीका अरस्तू द्वारा 2000 वर्ष पूर्व कही गई बात को बखूबी प्रतिध्वनित करता था: “यदि आप कुछ समझना चाहते हो, तो उसकी शुरुआत और उसके विकास को देखो।”
स्कूलों में बच्चे गणित कैसे सीखते हैं, इसे लेकर हुए अनुसन्धान दर्शाते हैं कि क्यों इसके शिक्षण में इतिहास महत्व रखता है। यह हमें कई अलग-अलग तरीकों से ‘क्यों’ का जवाब देने में मदद कर सकता है। सबसे पहले, बच्चों के मन में ऐतिहासिक तथ्यों को लेकर कई ‘क्यों’ प्रश्न होते हैं। यदि आपको अपने स्कूल दिन याद हैं तो हम सभी के मन में ऐसे सवाल होते थे। इनमें इस तरह के सवाल शामिल होते हैं: “समकोण 90 डिग्री का ही क्यों होता है? एक मिनट में 60 सेकण्ड और 1 घण्टे में 60 मिनट क्यों होते हैं?” कोई जानकार शिक्षक इस बात पर प्रकाश डाल सकता है कि गणित में ये परिभाषाएँ कैसे विकसित हुईं और ये ज़रूरी क्यों हैं, हालाँकि अधिकांश मामलों में ये मनमानी ही होती हैं।

दूसरा, और शायद सबसे महत्वपूर्ण, बच्चे विषय के हिस्सों और अवधारणाओं के बारे में ‘क्यों’ पूछते हैं। मसलन, हमें बीजगणित की ज़रूरत क्यों है? केल्कुलस की क्या ज़रूरत है? ये किस काम आते हैं? इनका विकास कैसे हुआ? इस विषय में नए विचारों के विकास के पीछे प्रमुख व्यक्तियों के साथ-साथ सदैव एक पृष्ठभूमि होती है। इस पृष्ठभूमि को समझने से हमें विभिन्न विषयों के बीच गणितीय कड़ियाँ जोड़ने में मदद मिलती है। इससे यह भी पता चलता है कि विभिन्न विचारों के विकास को कहाँ से स्फूर्ति मिली थी। और सबसे बड़ी बात यह है कि इससे विषयवस्तु का मानवीयकरण होता है।
गणितीय विषयों या विचारों की उपयोगिता के सवाल को दो तरह से सम्बोधित किया जा सकता है। किसी ‘खालिस’ गणितज्ञ के लिए किसी नए विचार अथवा महत्वपूर्ण गणितीय खोज से स्वयं गणित के उद्देश्य की पूर्ति होती है, चाहे वह मानव कल्याण अथवा वैज्ञानिक विकास में कोई योगदान दे या न दे। ‘प्रायोगिक’ गणितज्ञ को लिए प्रमुख सरोकार सदा यह रहता है कि गणित को समाज की बेहतरी के लिए कैसे इस्तेमाल किया जा सकता है। यह सरोकार काफी व्यापक है, इसमें विज्ञान, इंजीनियरिंग, सामाजिक विज्ञान, कला और वाणिज्य - दरअसल मानवीय क्रियाकलाप का हर पहलू शामिल होता है।

कोई भी नया टॉपिक उठाते समय, चन्ना शुरू की कुछ कक्षाओं में हमें उससे जुड़ी कहानियाँ सुनाते थे। वे समझाते थे कि कैसे और क्यों कोई विचार समय के साथ विकसित हुआ और यह भी बताते थे कि उसके विकास में प्रमुख व्यक्ति कौन थे। वे अपनी बात को इतना सरल रखते थे कि हम मूल विचार को पकड़ पाएँ। जैसे-जैसे कहानी आगे बढ़ती, धीमे-धीमे, किन्तु निश्चित रूप से, वे हमें यह समझा देते थे कि हम अब कक्षा में जो कुछ करने जा रहे हैं (या करने भी लगे हैं), उसका इस विचार से क्या सम्बन्ध है।
गणितीय कड़ियों और परिप्रेक्ष्यों की इस विहंगम दृष्टि से लैस होकर हम समस्या समाधान में जुट जाते, जो ज़्यादा ढर्रेनुमा होता था मगर उतना ही महत्वपूर्ण हिस्सा होता था। कहानियाँ हमारे साथ लम्बे समय तक बनी रहतीं। मुझे वे कहानियाँ इतने वर्षों बाद भी याद हैं क्योंकि वे मुझे सोचने और कल्पना करने को उकसाती रहती हैं।

गणित सीखने का उद्देश्य
हम देख पाते थे कि गणित कोई अलग-थलग बक-बक नहीं है। इसकी उत्पत्ति विभिन्न संस्कृतियों में, अलग-अलग समय पर इन्सानों के विभिन्न उद्देश्यों की पूर्ति के लिए हुई है और इसने मनुष्य के ज्ञान व अनुभव को विस्तार दिया है। उद्देश्य शुद्धत: बौद्धिक हो सकता है अथवा समाज में किसी विशिष्ट समस्या को सुलझाने का हो सकता है, या वैज्ञानिक विचारों के विकास में मदद का हो सकता है।
इस प्रकार से गणित मानव समाज के साथ अभिन्न रूप से जुड़ा है। इसका प्रादुर्भाव लोगों के सवालों के जवाब देने और विभिन्न किस्म की समस्याओं को सुलझाने के लिए हुआ था। जैसे-जैसे ज़्यादा सवाल और समस्याएँ उभरीं, वैसे-वैसे गणित का विकास होता गया। यह मानव जीवन के समक्ष उपस्थित चुनौतियों के समाधान हेतु नए-नए विचारों का आविष्कार करता जा रहा है। यदि बच्चे इस बात को देख सकें तो गणित सीखना उतना ही अधिक उद्देश्यपूर्ण हो सकता है और इसे सीखने के लिए एक अच्छी बुनियाद तैयार की जा सकती है।

मैं यह नहीं कह रहा हूँ कि इतिहास ही सब कुछ है। लेकिन यह एक महत्वपूर्ण हिस्सा है जो इस विषय को सीखने-सिखाने की पहेली में से नदारद है। इतिहास दुधारी तलवार जैसा (dicey) है, जैसा कि हमने पिछले अध्याय में युक्लिड के प्रकरण में देखा था। यह तब और भी पेचीदा हो जाता है जब हम राजनैतिक भूगोल को शामिल कर लेते हैं। इसकी बात हम कुछ देर बाद करेंगे।
एक इन्सान के नाते और एक शिक्षक के नाते चन्ना निहायत आत्मविश्वासी और शान्त नज़र आते हैं। लगभग बुद्ध के समान वे निर्लिप्त हैं, मगर उष्णता बिखेरते हैं। हम उनके करीब नहीं आ सकते और न ही दोस्ताना हो सकते हैं। वे सुनिश्चित करते हैं कि हमारे और उनके बीच हमेशा एक दूरी बनी रहे। मेरा ख्याल है, यह ठीक ही है। लेकिन जब उनके साथ गणित सीखने की बारी आती है, तो मज़ा ही मज़ा होता है। थोड़े गंजे सिर, चश्मे और नफीस सूट में वे आदर्श गणितज्ञ लगते हैं!
हर दिन सुबह चन्ना अपने लम्ब्रेटा स्कूटर पर स्कूल आते हैं। उनके दिमाग में क्या चलता है और हर दिन वे हमारे लिए क्या खिचड़ी पकाते हैं?
जब मैं पीछे मुड़कर उन तीन वर्षों को देखता हूँ, जब उन्होंने हमें पढ़ाया था, तो मुझे समझ में आता है कि वे विषय के ज्ञान में कितने पारंगत थे। इतने सालों बाद मुझे समझ में आया है कि वे वास्तव में गणितीय विश्व और उसके शाश्वत रहस्यों और विरोधाभासों के अन्वेषी थे।

शेषागिरी केएम राव: यूनीसेफ, छत्तीसगढ़ में शिक्षा विशेषज्ञ हैं। प्रारम्भिक शिक्षा और बाल्यावस्था में विकास में विशेष रुचि। साथ ही, आधुनिक शैक्षिक मुद्दों पर लिखने में दिलचस्पी।
अँग्रेज़ी से अनुवाद: सुशील जोशी: एकलव्य द्वारा संचालित स्रोत फीचर सेवा से जुड़े हैं। विज्ञान शिक्षण व लेखन में गहरी रुचि।
यह लेख और इसके चित्र एकलव्य द्वारा प्रकाशित पुस्तक द मैन हू टॉट इंफिनिटी से साभार।