अजय शर्मा
 फर्ज़ कीजिए कि आप और मैं पैदल सैर पर निकले हैं। गप्पों का सिलसिला पूरे ज़ोरों पर है और ऐसे में मैं आप से कहता हूं, “क्या आप को मालूम है कि इस समय धरती और आप की नाक की ऊंचाई के बीच करीब 200 वोल्ट का विद्युत विभव अंतर है।” मुमकिन है कि आपको लगे कि मैं फिर कोई नई ‘ढील’ दे रहा हूं! आप तत्काल कुछ प्रश्न दाग देंगे। मसलन, “अच्छा अगर ऐसा है तो हर बार जब हम घर से निकलते हैं तो दो सौ वोल्ट का करारा झटका क्यों नहीं लगता?” हो सकता है कि आप यह भी फरमाएं, “जब ऐसा ही है तो हम बिजली की कमी का रोना क्यों रोते हैं। दो इलेक्ट्रोड को दो-मीटर की ऊंचाई के अंतर पर हवा में टांग कर जब मन करे, मुफ्त में बिजली प्राप्त क्यों नहीं कर लेते हैं? सवाल बिलकुल वाजिब है। पर हाजुर गप्प तो मैं भी नहीं मार रहा हूं।
फर्ज़ कीजिए कि आप और मैं पैदल सैर पर निकले हैं। गप्पों का सिलसिला पूरे ज़ोरों पर है और ऐसे में मैं आप से कहता हूं, “क्या आप को मालूम है कि इस समय धरती और आप की नाक की ऊंचाई के बीच करीब 200 वोल्ट का विद्युत विभव अंतर है।” मुमकिन है कि आपको लगे कि मैं फिर कोई नई ‘ढील’ दे रहा हूं! आप तत्काल कुछ प्रश्न दाग देंगे। मसलन, “अच्छा अगर ऐसा है तो हर बार जब हम घर से निकलते हैं तो दो सौ वोल्ट का करारा झटका क्यों नहीं लगता?” हो सकता है कि आप यह भी फरमाएं, “जब ऐसा ही है तो हम बिजली की कमी का रोना क्यों रोते हैं। दो इलेक्ट्रोड को दो-मीटर की ऊंचाई के अंतर पर हवा में टांग कर जब मन करे, मुफ्त में बिजली प्राप्त क्यों नहीं कर लेते हैं? सवाल बिलकुल वाजिब है। पर हाजुर गप्प तो मैं भी नहीं मार रहा हूं।
दरअसल, अपना वायुमंडल है ही ऐसी पेचीदा और अजीबोगरीब ‘वस्तु’। इसके अनेक पहलू हमें बेहद आश्चर्यजनक ही लगते हैं। ऊपर दागे गए प्रश्न इनमें से एक बेहद दिलचस्प पहलू को उजागर करते हैं। यह लेख इसी पहलू पर केन्द्रित है। पर आपके सवालों के जवाब देने से पहले बेहतर होगा कि हम विद्युत विभव और विद्युत धारा जैसी अवधारणाओं के बारे में अपनी समझ फिर तरोताज़ा कर लें। इससे हमें वायुमंडल के विद्युतीय गुणधर्मों#ं को सुगमता से समझने में मदद मिलेगी।
क्या आप अंदाज़ा लगा सकते हैं कि धरती और वायुमंडल की ‘छत’ के बीच कुल कितना विद्युत अंतर होगा? चौंकिए नहीं, यह अंतर मात्र 4,00,000 वोल्ट का ही होता हे। इस विभव अंतर की उत्पत्ति को समझना थोड़ा पेचीदा मसला है। पर एक मोटे तौर पर हम कह सकते हैं कि यह विद्युत विभव अंतर इसलिए मौजूद होता है क्योंकि धरती की सतह का कुल आवेश ऋणात्मक है और वायुमंडल की किसी भी परत का कुल आवेश धनात्मक।
आवेश का प्रभाव क्षेत्र
जैसा कि संदर्भ पत्रिका के सातवें अंक में प्रकाशित ‘बिजली और आवेश’ लेख में मैंने ज़िक्र किया था - प्रकृति में कई कण एक ‘विशेष’ गुणधर्म प्रदर्शित करते हैं जिसे हम विद्युत आवेश के नाम से पहचानते हैं। सरल शब्दों में, विद्युत आवेश वह गुणधर्म है जिसके कारण आवेशित कण (यानी जिन पर आवेश होता है) एक दूसरे पर विद्युत या विद्युत चुम्बकीय बल - आकर्षण या विकर्षण - डालते हैं। विद्युत आवेश दो किस्म का होता है - धन और ऋण। समान आवेश धारण किए कण एक दूसरे को विकर्षित करते हैं और असमान रूप से आवेशित कण एक दूसरे को आकर्षित।
*विद्युत आवेश का मापन कूलंब नामक इकाई में किया जाता है।
आवेशित कण एक दूसरे पर यह बल विद्युत क्षेत्र की मदद से लगाते हैं। दरअसल होता यह है कि हरेक आवेशित कण अपने चारों ओर एक विद्युत क्षेत्र को जन्म देता है। अब अगर इस क्षेत्र में कोई दूसरा आवेशित कण भी मौजूद है तो उस पर एक विद्युत या विद्युत-चुम्बकीय बल ज़रूर लगेगा। यह बल कितना और किस दिशा में लगेगा यह इस बात पर निर्भर करता है कि उस बिन्दु (जहां पर दूसरा आवेशित कण मौजूद है) पर विद्युत क्षेत्र का मान और दिशा क्या है। विद्युत क्षेत्र के मान से हमारा तात्पर्य उस बिन्दु पर लगने वाले विद्युत बल प्रति आवेश से है।
जब जिस तरह किसी चुम्बक के चुम्बकीय क्षेत्र को हम अक्सर बल रेखाओं द्वारा दर्शाते हैं, उसी तरह किसी विद्युत क्षेत्र को दर्शाने के लिए भी विद्युतीय बल रेखाओं का उपयोग काफी प्रचलित है (चित्र-1अ, ब और स)।
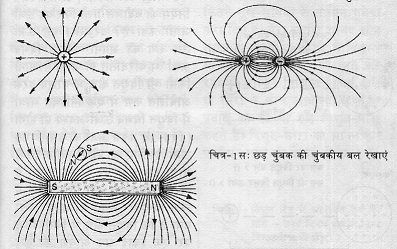 चित्रात्मक प्रस्तुति करते वक्त बल रेखाओं की आपस में दूरी विद्युत बल की शक्ति का प्रतीक है।* यानी अगर किसी जगह यह बल रेखाएं थोड़ी दूरी पर बनाई गई हैं या थोड़ी बिखरी हुई हैं तो वहां पर विद्युत बल कमज़ोर होगा, और अगर बल रेखाएं पास-पास सटी हुई बनाई गई हैं तो उसका अर्थ है कि वहां विद्युत बल का मान ज़्यादा होगा। एक पृथक आवेश की बल रेखाएं अनंत तक जाती हैं। जबकि दो या अधिक विपरीत आवेशों के विद्युत क्षेत्र को उन बल रेखाओं द्वारा दर्शाया जाता है जो धनात्मक आवेश से निकल कर ऋणात्मक आवेश पर खत्म होती हैं।
चित्रात्मक प्रस्तुति करते वक्त बल रेखाओं की आपस में दूरी विद्युत बल की शक्ति का प्रतीक है।* यानी अगर किसी जगह यह बल रेखाएं थोड़ी दूरी पर बनाई गई हैं या थोड़ी बिखरी हुई हैं तो वहां पर विद्युत बल कमज़ोर होगा, और अगर बल रेखाएं पास-पास सटी हुई बनाई गई हैं तो उसका अर्थ है कि वहां विद्युत बल का मान ज़्यादा होगा। एक पृथक आवेश की बल रेखाएं अनंत तक जाती हैं। जबकि दो या अधिक विपरीत आवेशों के विद्युत क्षेत्र को उन बल रेखाओं द्वारा दर्शाया जाता है जो धनात्मक आवेश से निकल कर ऋणात्मक आवेश पर खत्म होती हैं।
चित्र-1अ: एक धन आवेश की बल रेखाएं
चित्र-1ब: धन और ऋण आवेश के बीच विद्युत बल रेखाएं
चित्र-1स: छड़ चुंबक की चुंबकीय बल रेखाएं
*विज्ञान की और बहुतेरी मान्यताओं की तरह यह भी एक मान्यता है।
विभव: आखिर क्या बला है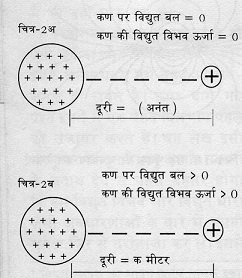 आइए अब देखते हैं कि विद्युत विभव की अवधारणा विद्युत क्षेत्र के सिद्धांत से कैसे उत्पन्न होती है। किसी भी विद्युत क्षेत्र की एक खासियत यह भी होती है कि किसी भी आवेशित पिंड का विद्युत क्षेत्र दूरी के साथ क्षीण होता जाता है और अनंत दूरी पर जाकर लुप्त हो जाता है। अब फर्ज़ कीजिए कि एक आवेशित कण चित्र में दर्शाए आवेशित पिंड से अनंत दूरी पर स्थित है। दोनों धनात्मक रूप से आवेशित हैं, पर पिंड का आवेश कण के आवेश से कहीं ज़्यादा (चित्र 2अ)।
आइए अब देखते हैं कि विद्युत विभव की अवधारणा विद्युत क्षेत्र के सिद्धांत से कैसे उत्पन्न होती है। किसी भी विद्युत क्षेत्र की एक खासियत यह भी होती है कि किसी भी आवेशित पिंड का विद्युत क्षेत्र दूरी के साथ क्षीण होता जाता है और अनंत दूरी पर जाकर लुप्त हो जाता है। अब फर्ज़ कीजिए कि एक आवेशित कण चित्र में दर्शाए आवेशित पिंड से अनंत दूरी पर स्थित है। दोनों धनात्मक रूप से आवेशित हैं, पर पिंड का आवेश कण के आवेश से कहीं ज़्यादा (चित्र 2अ)।
ऐसी स्थिति में कण पर पिंड के आवेश के कारण लगने वाला विद्युत विकर्षण बल भी शून्य ही होगा। अब हम कण को पिंड की ओर खिसकाना शुरू करते हैं। ज़ाहिर है कि जैसे-जैसे कण पिंड के करीब आता जाएगा, उस पर न सिर्फ विद्युत विकर्षण बल लगने लगेगा, बल्कि वह बल घटती हुई दूरी के साथ बलवती भी होता जाएगा। यानी अगर हम आवेशित कण को पिंड की ओर ढकेलते हैं तो हमें विद्युत विकर्षण के खिलाफ ऊर्जा व्यय करनी पड़ेगी। अब इस काम में हम जितनी भी ऊर्जा खर्च करते हैं, वह नष्ट तो हो नहीं सकती। (ऊर्जा संरक्षण नियम की बदौलत)। तो फिर वह ऊर्जा जाती कहां है? दरअसल यह ऊर्जा उस कण की अपनी ‘विद्युत विभव ऊर्जा’ में परिवर्तन हो जाती है। यानी किसी भी विद्युत क्षेत्र में मौजूद हरेक आवेशित कण में एक निश्चित मात्रा में विद्युत विभव ऊर्जा अवश्य ही होगी (चित्र-2ब)। इस ऊर्जा को हम ‘विभव ऊर्जा’ के लिए कह रहे हैं क्योंकि इसकी मात्रा इस बात पर निर्भर करती है कि वह आवेशित कण विद्युत क्षेत्र में किस बिन्दु पर स्थित है। अक्सर देखा गया है कि विद्युत क्षेत्र में किसी बिन्दु पर एक इकाई धन आवेश की कुल विद्युत विभव ऊर्जा कितनी होगी, यह जानना वैज्ञानिकों को विद्युत संबंधी सवालों का हल ढूंढने में काफी उपयोगी साबित होता है। इसलिए इस मात्रा को भौतिकी में एक अलग से नाम दिया गया है - विद्युत विभव।
किसी बिन्दु का विद्युत विभव = उस बिन्दु पर उपस्थ्ति आवेशित कण की कुल विद्युत विभव ऊर्जा / उस कण का कुल आवेश
विद्युत विभव का मापन वोल्ट नाम की इकाई में होता है। इसलिए विद्युत विभव को अक्सर ‘वोल्टेज’ के नाम से भी जाना जाता है।
हमारी अब तक चर्चा से स्पष्ट है कि विद्युत क्षेत्र में किसी भी बिन्दु पर विद्युत क्षेत्र (यानी विद्युत बल/आवेश) जितना अधिक प्रबल होगा, उस बिन्दु का विद्युत विभव भी उतना ही अधिक होगा। अब फर्ज़ कीजिए कि एक विद्युत क्षेत्र में दो बिन्दु हैं ‘अ’ और ’ब’ (चित्र-3)। इस विद्युत क्षेत्र में हम एक आवेशित कण को ‘अ’ बिन्दु पर इधर-उधर विचरने के लिए खुला छोड़ देते हैं। मान के चलिए कि इस कण पर विद्युत बल के अलावा और कोई बल नहीं लग रहा है। कण को ‘अ’ बिन्दु पर छोड़ते ही हम देखते हैं कि वह ‘ब’ बिन्दु की ओर भाग उठता है।
अब बताइए कि किस बिन्दु का विद्युत विभव ज़्यादा होगा? ‘अ’ का या ‘ब’ का?
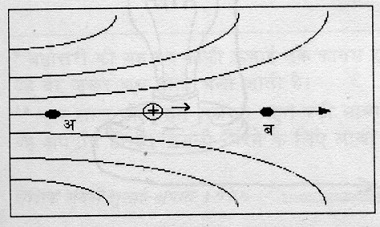 ज़ाहिर है, विद्युत विभव ‘अ’ का ही ज़्यादा ही होगा। आवेशित कणों को हम ज़्यादा वोल्टेज से कम वोल्टेज की ओर ही दौड़ता पाते हैं। एक तरह से देखा जाए तो आवेशित कणों का यह गुण हमारे लिए किसी वरदान से कम नहीं है। दो विभिन्न विद्युत विभव वाले बिन्दुओं के बीच आवेशित कणों को बहा कर वैज्ञानिकों ने हमें न जाने कितनी सुख-सुविधा के सामान मुहैया करा दिए हैं। मेरा इशारा शायद आप समझ ही गए होंगे। जी हां, मैं विद्युत-धारा (या करंट) की ही बात कर रहा हूं। आखिर विभिन्न विभव वाले दो सिरों के बीच आवेशित कणों के प्रवाह को ही तो हम विद्युत-धारा कहते हैं। विद्युत-धारा का मापन हम एम्पीयर नाम की इकाई में करते हैं।
ज़ाहिर है, विद्युत विभव ‘अ’ का ही ज़्यादा ही होगा। आवेशित कणों को हम ज़्यादा वोल्टेज से कम वोल्टेज की ओर ही दौड़ता पाते हैं। एक तरह से देखा जाए तो आवेशित कणों का यह गुण हमारे लिए किसी वरदान से कम नहीं है। दो विभिन्न विद्युत विभव वाले बिन्दुओं के बीच आवेशित कणों को बहा कर वैज्ञानिकों ने हमें न जाने कितनी सुख-सुविधा के सामान मुहैया करा दिए हैं। मेरा इशारा शायद आप समझ ही गए होंगे। जी हां, मैं विद्युत-धारा (या करंट) की ही बात कर रहा हूं। आखिर विभिन्न विभव वाले दो सिरों के बीच आवेशित कणों के प्रवाह को ही तो हम विद्युत-धारा कहते हैं। विद्युत-धारा का मापन हम एम्पीयर नाम की इकाई में करते हैं।
चूंकि कई किस्म के कणों पर आवेश हो सकता है, इसलिए संभव है कि अलग-अलग पदार्थों में करंट अलग-अलग किस्म के आवेशित कणों के प्रवाह के कारण हो। मसलन, धातुओं (जैसे तांबे के तार) में विद्युत धारा प्रवाह इलेक्ट्रॉन नाम के ऋण आवेशित कणों के बहने से ही होता है। तरल पदार्थों में या वायुमंडल में एक अलग तरह के आवेशित कणों, जिन्हें ‘आयन’ कहते हैं, का प्रवाह विद्युत-धारा बन सकता है।
गौर करें चित्र-4 अ, ब और स पर। चित्र में दर्शाई स्थिति से स्पष्ट है कि समय के साथ पानी के प्रवाह के कारण पानी तलों में, और उष्मा के बहने से दोनों छोरों के तापमान में अंतर घटने लगेगा, और अंतत: समानता आ जाएगी। लगभग ऐसा ही विद्युत प्रवाह के साथ होता है। यानी विद्युत प्रवाह भी दोनों बिन्दुओं (जिनके बीच करंट बह रहा है) के विद्युत विभव अंतर को खत्म कर देता है। ऐसे में विद्युत धारा प्रवाह भी अस्थाई ही होगा।
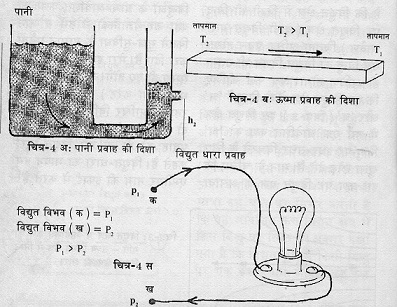
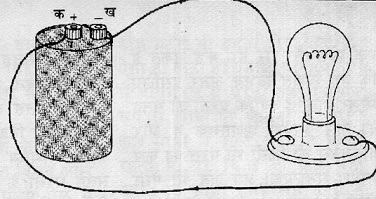 इसलिए अगर हम चाहते हैं कि करंट चालू रहे, तो कुछ ऐसा इंतज़ाम करना पड़ता है जिससे दोनों छोरों के बीचका विद्युत विभव अंतर यथावत कायम रहे। ऐसा हम दोनों छोरों को ‘वोल्टेज रुाोत’ नाम के साधन से जोड़ कर हासिल कर सकते हैं (चित्र-4द)। ‘वोल्टेज रुाोत’ विभव अंतर को एक निर्धारित मान पर बरकरार रखता है। वोल्टेज रुाोत कई प्रकार के होते हैं, जिनमें प्रमुख हैं ‘बैटरी’ और ‘जनरेटर’।
इसलिए अगर हम चाहते हैं कि करंट चालू रहे, तो कुछ ऐसा इंतज़ाम करना पड़ता है जिससे दोनों छोरों के बीचका विद्युत विभव अंतर यथावत कायम रहे। ऐसा हम दोनों छोरों को ‘वोल्टेज रुाोत’ नाम के साधन से जोड़ कर हासिल कर सकते हैं (चित्र-4द)। ‘वोल्टेज रुाोत’ विभव अंतर को एक निर्धारित मान पर बरकरार रखता है। वोल्टेज रुाोत कई प्रकार के होते हैं, जिनमें प्रमुख हैं ‘बैटरी’ और ‘जनरेटर’।
क्यों नहीं लगता झटका
वोल्टेज और करंट पर इस संक्षिप्त चर्चा के बाद आइए अब वापस चलें उन सवालों पर जो इस लेख की शुरूआत में हमने अनुत्तरित छोड़ दिए थे। यह बात बिलकुल सही है कि अगर आप किसी सामान्य दिन (यानी अब आपके ऊपर घनघोर बादल न छाए हों और बिजली न कड़क रही हो), किसी भी खुली जगह - ज़मीन या समुद्र की सतह - पर खड़े हैं तो आपके पैर और सिर की ऊंचाई के बीच 150-200 वोल्ट का विद्युत विभव अंतर ज़रूर होगा। दरअसल, हमारे वायुमंडल की यह अनूठी विशेषता है कि धरती की सतह से हर एक मीटर ऊपर जाने पर उस ऊंचाई का विद्युत विभव, धरती के बनिस्बत सौ वोल्ट से बढ़ जाता है। यानी अगर हम धरती का विद्युत विभव शून्य मान लें तो उससे एक मीटर की ऊंचाई पर वायुमंडल के हरेक बिन्दु का विद्युत विभव 100 वोल्ट (औसत मान) होगा। दो मीटर की ऊंचाई पर वोल्टेज 200 वोल्ट होगा। और इसी तरह आगे भी।*
क्या आप अंदाज़ा लगा सकते हैं कि धरती और वायुमंडल की छत के बीच कुल कितना विद्युत विभव अंतर होगा? चौंकिए नहीं, यह अंतर मात्र 4,00,000 वोल्ट का ही होता है।** इस विभव अंतर की उत्पत्ति को समझना थोड़ा पेचीदा मसला है। पर एक मोटे तौर पर हम कह सकते हैं कि यह विद्युत विभव अंतर इसलिए मौजूद होता है क्योंकि धरती की सतह का कुल आवेश ऋणात्मक है और वायुमंडल की किसी भी परत का कुल आवेश धनात्मक। अब जब भी ऐसा होता है यानी एक किस्म के आवेश एक छोर पर इकट्ठा हो जाते हैं और दूसरी किस्म के दूसरे छोर पर, तो उन दो छोरो के बीच विद्युत विभव अंतर पैदा होना स्वाभाविक है - ठीक किसी बैटरी की तरह।
अब पेश है आपके पहले सवाल का जवाब।
चूंकि धरती से एक ऊंचाई पर स्थित सभी बिन्दुओं का विद्युत विभव एक समान होता है हम वायुमंडल में विभिन्न ऊंचाईयों वाली अनेक सतहों की कल्पना कर सकते हैं। ऐसी हर काल्पनिक सतह पर विद्युत विभव का एक निश्चित मान होगा।। सबसे निचली सतह तो धरती ही होगी, और इसका विद्युत विभव होगा शून्य वोल्ट। सामान्य परिस्थितियों में यह सतहें धरती के समान्तर होती है, जैसा कि चित्र-5अ में दर्शाया गया है।
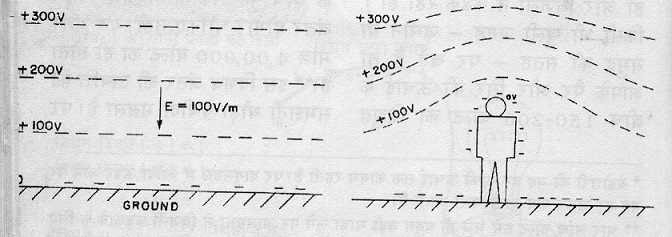
जब हम सपाट धरती पर कहीं खड़े होते हैं तो विद्युत विभव की स्थिति थोड़ी बदल जाती है। क्योंकि हमारा शरीर एक ठीक-ठीक सुचालक है इसलिए धरती पर मौजूदा ऋण आवेश हमारे शरीर पर भी फैल जाते हैं। फलस्वरूप हमारे शरीर के हर बिन्दु का विद्युत विभव धरती की सतह के विद्युत विभव के बराबर हो जाता है। लिहाज़ा सम विभव सतह (equipotential suface) भी थोड़ी टेढ़ी-मेढ़ी हो जाती है जैसे कि चित्र-5ब में दिखाया गया है। ऐसे हलातों में स्वाभाविक है कि हमारे सिर और पैर के बीच विद्युत विभव अंतर भी लगभग शून्य होगा।
चि-5 अ: धरती के ऊपर विद्युत विभव वितरण।
चि-5ब: विभव वितरण जब कम सपाट ज़मीन पर खड़े होते हैं।
हमारी पिछली चर्चा के अनुसार करंट बहने के लिए विद्युत विभव अंतर होना अनिवार्य है। इसलिए ऐसे में हमें बिजली का झटका भला क्यों लगे? दूसरे सवाल का उत्तर भी इसी जवाब में छुपा हुआ है। इसलिए आपके सिर खुजलाने के लिए मैं दूसरा सवाल अनुत्तरित ही छोड़ रहा हूं। उम्मीद है इसका हल आपको थोड़ी मेहनत-मशक्कत के बाद मिल ही जाएगा।
बढ़ोत्तरी का यह दर काफी ऊंचाई तक कायम रहती है। पर वायुमंडल में ज़यादा ऊपर जाने पर यह दर ज़रूर कम होती चली जाती है।
*चार लाख वोल्ट हमें भले ही बहुत बड़ी मात्रा लगे पर आसमान से बिजली कड़काने के लिए यह अपर्याप्त ही है। बिजली गिरने के लिए लाखों नहीं करोड़ों वोल्ट का विभव अंतर चाहिए।
धरती बनाम बैटरी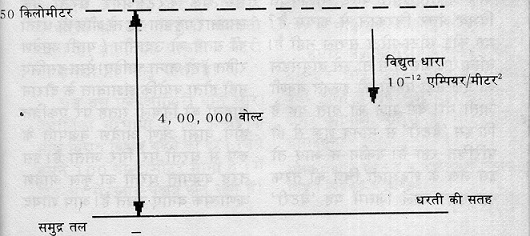 वैसे प्रश्नों का सिलसिला अभी खत्म नहीं हुआ है। ऊपर दिया गया हमारा जवाब कुछ और नए और दिलचस्प प्रश्न खड़े कर दता है। मसलन, जब आसमां और ज़मीन के बीच विद्युत विभव अंतर है तो क्या इन दोनों के बीच करंट भी बहता होगा? जी हां, ऐसा ही होता है। सामान्य परिस्थितियों में वायुमंडल से धरती तक धनात्मक रूप से आवेशित आयनों के ज़रिए कुछ मात्रा में करंट अनवरत बहता रहता है। पर चिंता की कोई बात नहीं, यह मात्रा बेहद कम होती है सिर्फ दस माइक्रो-माइक्रो एम्पियर प्रति वर्गमीटर क्षेत्रफल में लगभग 10-12 एम्पियर करंट ही प्रवेश कर पाता है। इसके लिए हमें शुक्रगुज़ार होना चाहिए वायु का, क्योंकि उसकी कुचालकता के कारण ही वायुमंडलीय करंट इतना क्षीण होता है।
वैसे प्रश्नों का सिलसिला अभी खत्म नहीं हुआ है। ऊपर दिया गया हमारा जवाब कुछ और नए और दिलचस्प प्रश्न खड़े कर दता है। मसलन, जब आसमां और ज़मीन के बीच विद्युत विभव अंतर है तो क्या इन दोनों के बीच करंट भी बहता होगा? जी हां, ऐसा ही होता है। सामान्य परिस्थितियों में वायुमंडल से धरती तक धनात्मक रूप से आवेशित आयनों के ज़रिए कुछ मात्रा में करंट अनवरत बहता रहता है। पर चिंता की कोई बात नहीं, यह मात्रा बेहद कम होती है सिर्फ दस माइक्रो-माइक्रो एम्पियर प्रति वर्गमीटर क्षेत्रफल में लगभग 10-12 एम्पियर करंट ही प्रवेश कर पाता है। इसके लिए हमें शुक्रगुज़ार होना चाहिए वायु का, क्योंकि उसकी कुचालकता के कारण ही वायुमंडलीय करंट इतना क्षीण होता है।
पर हमारी पूरी पृथ्वी तो बहुत विशाल है। उसकी सतह पर न जाने कितने वर्ग-मीटर होंगे। क्या आप अंदाज़ा लगा सकते हैं कि संपूर्ण धरती पर वायुमंडल से कुल कितना करंट लगातार बहता रहता होगा? यह मात्रा है सिर्फ 1800 एम्पीयर।
उम्मीद है कि आप सहमत होंगे अगर मैं अपनी इस पृथ्वी की एक विशालकाय विद्युतीय मशीन से तुलना करूं जिससे 4,00,000 वोल्ट पर 1800 एम्पियर करंट लगातार बहता रहता है। इस बैटरी की विद्युतीय शक्ति होगी - 4,00,000 वोल्ट X 1800 एम्पियर, यानी लगभग 700 मेगावॉट!
हमारा अनुभव है कि किसी भी बैटरी से अगर लगातार करंट बहता है तो उसे डिस्चार्ज होने यानी चुकने में ज़्यादा समय नहीं लगता। ऐसी गणना की गई है कि यदि ज़मीन और आसमां के बीच विद्युत-विभव अंतर किसी भी तरह बरकरार न रखा जाए, तो 1800 एम्पियर का वायुमंडलीय करंट मात्र आधें घंटे तक ही बहेगा। पर आधे घंटे से ज़्यादा समय तो मुझे यह लेख लिखते हुए ही हो गया है। तो फिर वह कौन-सी प्राकृतिक बैटरी है तो कभी डिस्चार्ज नहीं होती और जिसके ज़रिए ज़मीन और आसमां के बीच 4,00,000 वोल्ट या विद्युत विभव अंतर चिरकाल से कायम है? यह कोई छोटा-मोटा सवाल नहीं हैं। बल्कि एक ज़माने में तो इसे वायुमंडल की एक बड़ी पहेली की इज्जत बक्शी जाती थी। वैसे मज़े की बात यह है कि इस ‘बैटरी’ से मानव शुरू से ही परिचित रहा है। यकीन न आए तो इस लेख के शुरुआती चित्र की तरफ एक नज़र डालें यह ‘बैटरी’ दर्शाई गयी है। जी हां, झंझावात (Thunderstorm) और वज्रपात ही वह इंतज़ाम है जिसके कारण पृथ्वी की विद्युतीय मशीन कभी नहीं रुकती।
वैसे यह पूरा मसला काफी पेचीदा है, पर अगर एक प्राथमिक स्तर पर समझना चाहें तो माज़रा कुछ इस प्रकार है।
साधारणत: झंझावात में ऋण और धन आवेशों का संतुलन बिगड जाता है। धन आवेश बादलों के ऊपरी हिस्सों में पहुंच जाते हैं और ऋण आवेश निचले हिस्सों में इकट्ठा होने लगते हैं। फिर हवा के ज़रिए धन आवेश बादल के ऊपरी हिस्सों से निकल कर वायुमंडल की बहुत ऊंची परतों में बिखर जाते हैं। अब उन जगहों पर जहां मौसम साफ है यन धन आवेश 1800 एम्पियर धनात्मक करंट के रूप में धरती की सतह पर कुल आवेश तो ऋणात्मक है। 1800 एम्पियर का धनात्मक करंट अगर धरती तक लगातार पहुंचता रहे तो शीघ्र ही धरती की सतह को उदासीन (यानी आवेश रहित) हो जाना चाहिए। ऐसा इसलिए नहीं होता क्योंकि झंझावात के दौरान बादलों की निचली सतह पर एकत्रित होने वाला ऋण आवेश वज्रपात के रूप में धरती पर गिर जाता है। इस तरह वज्रपात धरती का कुल आवेश ऋणात्मक बनाए रखते है। आप शायद सोच रहे होंगे कि वायुमंडलीय करंट तो हर समय बहता रहता है, पर हम तो बिजली को साल भर में कुछ ही बार गिरता हुआ देखते हैं। पर ऐसा नहीं है। पूरी धरती को ध्यान में रख कर गणना की जाए तो मालूम पड़ता है कि एक दिन में करीब 40,000 झंझावात आते हैं, और एक सेकेण्ड में करीब सौ बार बिजली चमकती रहती है। यानी यह प्राकृति बैटरी भी हमेशा ही चालू रहती है।
. . . विद्युत विभव नापना
कई तरीके हैं जिनके द्वारा धरती से किसी भी ऊंचाई का वायुमंडलीय विभव मापा जा सकता हे। एक तरीका तो यही है कि आप किसी इन्सुलेट्ड सुचालक को धरती से उस ऊंचाई पर किसी प्रकार टांग दें। हालांकि वायु की सुचालकता काफी कम होती है, पर उस सुचालक को अगर हम काफी लंबे अर्से तक टंगा रहने दें, तो धीरे-धीरे उस सुचालक की सतह पर आवेश जमा होने लगेगा। यह सिलसिला तब तक चलेगा जब तकउस सुचालक का विद्युत विभव उस ऊंचाई के वायुमंडलीय विद्युत के बराबर नहीं हो जाता है। जब आप इस सुचालक को धरती पर उतारेंगे तो स्वाभाविक है कि उसका विद्युत विभव भी बदलेगा। विद्युत विभव के इस बदलाव को आप एक इलेक्ट्रोमीटर की मदद से नाप सकते हैं। चूंकि धरती का विद्युत विभव हम शून्य वोल्ट मान रहे हैं इसलिए मापी गई मात्रा उस ऊंचाई के वायुमंडलीय विद्युत विभव के बराबर ही होगी।
अब बस एक आखिरी बात और। वैज्ञानिकों ने पाया है कि ऊंचाई के साथ विद्युत विभव बढ़ने की दर (जिसे हमने 100 वोल्ट/मीटर माना है) में दिन-भर में उतार-चढ़ाव होते रहते हैं।
पर हैरत की बात यह है कि आप करंट का मापन धरती पर कहीं भी करें, हिंद महासागर में, अमेरिका में या एंटार्कटिका में, करंट अधिकतम और न्यूनतन तभी रहता है जब लंदन की घड़ियों में शाम को सात और सुबह के चार बज रहे होते हैं। यानी जब हमारी घड़ियों में दोहहर के डेढ़ और रात के साढ़े दस बज रहे होते हैं।
हमारे अजीबोगरीब वायुमंडल का यह एक और अनूठा पहलू है। ऐसा क्यों होता है यह मुझे नहीं मालूम, अगर आपको मालूम हो तो ज़रूर बताइएगा।
अजय शर्मा - एकलव्य के होशंगाबाद विज्ञान शिक्षण कार्यक्रम में कार्यरत।


