सुशील जोशी
पिछले अंक में मैंने एवोगैड्रो संख्या की सैद्धांतिक चर्चा की थी और वायदा किया था प्रायोगिक रूप से इसके निर्धारण की बात अगले अंक में करेंगे। वह अंक अब आ पहुंचा है।
एवोगैड्रो संख्या का मतलब होता है किसी भी पदार्थ के एक मोल में उपस्थित कणों की संख्या (ये कण अणु, परमाणु या आयन हो सकते हैं)। यह तो आप जानते ही हैं कि यह संख्या काफी विशाल है। आप यह भी जानते ही हैं कि जिन कणों की बात हो रही है वे अत्यंत सूक्ष्म हैं और आम-संतरों की तरह इन्हें गिनना असंभव ही होगा (चाहे शिक्षा विभाग के सारे शिक्षकों को लगा दिया जाए)। इनकी गिनती अप्रत्यक्ष रूप से की जाती है और गिनती करने के लिए कई मान्यताएं लेकर चलना होता है। इस अंक में मैं इस संख्या को ज्ञात करने के लिए प्रयुक्त की गई पहली विधि की चर्चा करूंगा।
यह विधि फ्रांसीसी वैज्ञानिक ज़्यां पेरिन ने खोजी थी और उपयोग की थी। बात 20वीं सदी के शुरु की है। पेरिन ने इस काम के लिए भौतिकी के कई सिद्धांतों व अवलोकनों की मदद ली थी। सबसे पहले तो उन्हें गैसों के अणु गति सिद्धांत से मदद मिली थी। दूसरा, उन्हें इस बात से मदद मिली थी कि वान्ट हॉफ ने दर्शाया था कि गैस का अणु गति सिद्धांत तनु विलयनों पर भी लागू होता है। और अंतत: उनका पूरा प्रयोग इस मान्यता पर टिका था कि तनु विलयन पर और गैसों पर लागू होने वाले सिद्धांत कोलॉइड्स (इमल्शन्स) पर भी लागू होते हैं।
गैसों का सिद्धांत
दरअसल परमाणु सिद्धांत को स्थापित करने के लिए ज़रूरी था कि डाल्टन ने जिन परमाणुओं की बात की थी या एवोगैड्रो ने जिन अणुओं की बात की थी, उनका डील-डौल तो कुछ पता चले, सिर्फ अनुपातों से काम नहीं चल सकता था। यानी सिर्फ यह कहना काफी नहीं है कि ऑक्सीजन का एक अणु हाइड्रोजन के एक अणु से 16 गुना भारी है।
इस मामले में सबसे पहला प्रयास गैसों के दबाव की व्याख्या के रूप में किया गया था। गैसों के कण-गति सिद्धांत में मान्यता यह थी कि गैसें लचीले अणुओं से मिलकर बनी हैं और ये कण लगातार गति करते रहते हैं। ये किसी अन्य कण से टकराने से पहले सीधी रेखा में चलते रहते हैं। बगैर टकराए कोई कण जितनी औसत दूरी तय करता है उसे औसत मुक्त पथ कहते हैं। गैसों का दबाव इन कणों के दीवार से टकराने के कारण होता है। इस सिद्धांत और प्रायोगिक अवलोकनों के बीच काफी सामंजस्य देखा गया था।
क्लॉसियस ने दर्शाया था कि गैस के अणु जितने छोटे होंगे, औसत मुक्त पथ उतना अधिक होगा। यानी यदि हमें औसत मुक्त पथ पता हो तो हम गैस की निश्चित मात्रा में अणुओं की कुल सतह की गणना कर सकते हैं। यह माना जा सकता है कि अणुओं का कुल आयतन शायद उतनी ही गैस को ठोस बनाकर नापे गए आयतन से बहुत भिन्न नहीं होगा। तो इस तरह से हम गैस की उस संहति में अणुओं की संख्या भी निकाल सकेंगे और उनका व्यास भी निकाल सकेंगे।
इस तरह से गणना करने पर अणुओं का व्यास (अलग-अलग गैसों के लिए) मिलीमीटर का 1 करोड़वां भाग निकला। और एवोगैड्रो संख्या 40 x 1022 और 120 x 1022 के बीच निकाली गई थी। मगर ये गणनाएं करने के लिए कई सारी मान्यताएं स्वीकार करनी पड़ी थीं। जैसे अणुओं को गोलाकार मानना पड़ा था।
इससे अलग पेरिन की विधि मूलत: किसी इमल्शन में कणों के अवक्षेपित होने की दर पर आधारित थी। इस विधि का तार्किक आधार कई राहों से मिला था।
गैसें और तनु विलयन
इस सम्बन्ध को आप ध्यान में रखें, और हम तर्क के अगले सोपान पर चलते हैं। अणु गति सिद्धांत के मुताबिक गैसों का दबाव उनके अणुओं की गति के कारण होता है। वांट हॉफ नामक एक रसायन शास्त्री ने दर्शाया था कि गैस का यह सिद्धांत तनु विलयनों पर भी लागू होता है। वांट हॉफ ने यह भी स्पष्ट किया था कि यदि तनु विलयन को ऐसे पात्र में रखा जाए जिसकी दीवारें विलायक के अणुओं को तो गुज़रने दें मगर विलेय के अणुओं को रोकें (अर्ध-पारगम्य दीवार) तो विलेय के अणु (गैस के अणुओं के समान) ऐसे पात्र की दीवार पर एक दबाव डालते हैं (जिसे हम परासरण दबाव कहते हैं)। यह दबाव ठीक उतना होता है जितना विलेय के उतने ही अणु गैसीय अवस्था में होने पर (यानी विलायक के बगैर) पात्र की दीवारों पर डालेंगे। यानी एवोगैड्रो का सिद्धांत तनु विलयनों पर लागू होता है।
पेरिन ने इस बात को आगे बढ़ाते हुए माना था कि यह नियम इमल्शन। पर भी लागू होना चाहिए। इमल्शन यानी कोई पदार्थ किसी अन्य पदार्थ में घुला तो नहीं है मगर टंगा है। जैसे दूध एक इमल्शन है। यानी एवोगैड्रो के नियम को हम विस्तार दे सकते हैं: अणुओं की बराबर संख्या, चाहे गैसीय अवस्था में हो या घुलित अवस्था में, समान आयतन व तापमान पर बराबर दबाव डालेगी। यानी दबाव सिर्फ कणों की संख्या से तय होता है, उनके आकार अथवा वज़न से नहीं।
पता करें एवोगैड्रो संख्या
तो यह एवोगैड्रो संख्या ज्ञात करने का आसान तरीका हो सकता है। एक ऐसे पदार्थ का इमल्शन बनाएं जिसके कण बड़े-बड़े हों। अब इसे किसी अर्ध पारगम्य दीवार वाले पात्र में रख दें। आप परासरण दाब नाप लें और चूंकि कण बड़े-बड़े हैं इसलिए प्रति घन सेंटीमीटर आयतन में इनकी संख्या गिनी जा सकेगी। यानी इतने ही दबाव वाली किसी भी गैस में कणों की संख्या बराबर होगी। इसके आधार पर यह गणना की जा सकती है कि सामान्य दाब (वायुमंडलीय दाब) पर 1 मिलीलीटर गैस में कितने अणु होंगे और फिर यह पता लगाया जा सकता है कि 22,400 मिलीलीटर गैस (यानी 1 मोल गैस) में कितने अणु होंगे। मगर इस विधि का उपयोग करने में व्यावहारिक कठिनाइयां हैं। आपको बहुत तनु विलयन की ज़रूरत होगी। यदि विलयन बहुत तनु हुआ तभी तो आप कणों को गिन पाएंगे। मगर इमल्शन जितना तनु होगा उसका परासरण दाब उतना ही कम होता जाएगा और उसे सटीकता से नापना उतना ही मुश्किल होता जाएगा।
तो पेरिन इमल्शनों के किसी ऐसे गुण की तलाश में थे जो गैस नियमों के अनुरूप हो और प्रायोगिक रूप से नापने योग्य हो। सन् 1908 में उन्होंने यह गुण खोज निकाला।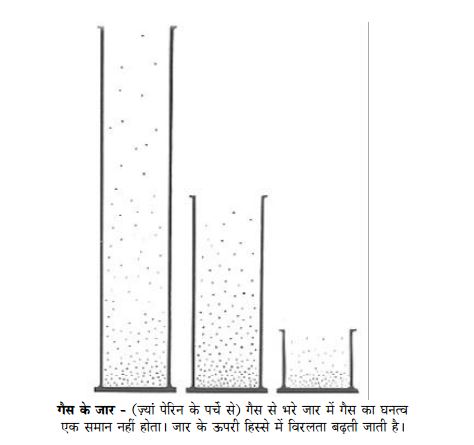
एक और नियम
पहले तो गैसों के व्यवहार पर ध्यान दें। यदि कोई गैस किसी बर्तन में भरी जाती है, तो वह पूरे बर्तन में फैल जाती है। मगर यदि बर्तन बहुत गहरा हो, तो पूरे बर्तन में गैस का घनत्व एक समान नहीं होता। जैसे-जैसे आप ऊपर की ओर जाएंगे गैस का घनत्व कम होता जाएगा। जैसे जब आप सीढ़ी की एक पायदान चढ़ते हैं तो हवा के दबाव में पहली पायदान से 1/40,000 भाग की कमी आती है। हर पायदान चढ़ने पर इतनी कमी आती है। इस कम होते जाने का एक नियमित क्रम होता है। यानी यदि आप समुद्र तल से शुरु करें तो एक निश्चित ऊंचाई पर गैस का घनत्व आधा रह जाता है। फिर उतनी ही ऊंचाई और चढ़ें तो फिर से घनत्व आधा रह जाएगा। यानी गैस की विरलता बढ़ती जाती है।
इस सम्बंध में एक बात यह पहचानी गई थी कि ऊंचाई के साथ गैस की विरलता बढ़ने की दर गैस के अणु भार पर निर्भर करती है। जैसे ऑक्सीजन का उदाहरण लें तो हरेक 5 किलोमीटर की ऊंचाई पर उसका दबाव पहले से आधा रह जाता है। एवोगैड्रो के नियम के अनुसार इसका मतलब है कि उसमें बराबर आयतन में अणुओं की संख्या पहले से आधी रह गई है। यदि हाइड्रोजन गैस की बात करें तो उसका दबाव आधा होने के लिए हमें 80 किलोमीटर की ऊंचाई चढ़ना पड़ेगी क्योंकि हाइड्रोजन का अणु भार ऑक्सीजन से 16 गुना कम है।
वान्ट हॉफ के मुताबिक यह नियम तनु विलयनों पर भी लागू होता है। पेरिन ने माना कि यह नियम इमल्शन पर भी लागू होता है। हमारे पास एक स्थिर इमल्शन है जिसके सारे कण एक ही आकार के हैं। इसे हम कुछ समय के लिए एक स्थिर तापमान पर रखा रहने देते हैं। यानी इसके कणों पर सिर्फ गुरुत्व का असर हो रहा है। अब ये कण अपनी स्वतंत्र गति करते हैं, बिल्कुल गैसों की तरह। अंतर सिर्फ इतना है कि गैसों के कण शून्य में विचरते हैं और इमल्शन के कणों के आसपास विलायक के अणुओं का परिवेश है। विलायक की उपस्थिति का असर यह होता है कि इमल्शन के अणुओं पर आर्किमिडीज़ के नियम के मुताबिक उछाल बल लगता है। इसका परिणाम यह होता है कि इन कणों का प्रभावी भार उतना कम हो जाता है।
अब यदि हमारी मान्यता सही है कि ऊंचाई के साथ विरलता बढ़ने का नियम इमल्शन पर भी लागू होता है, तो संतुलन स्थापित हो जाने के बाद हमारे इमल्शन के इस लघु वातावरण में एक निश्चित ऊंचाई पर विरलता एक निश्चित मान से बढ़ेगी। यदि विरलता को दुगना करने के लिए हमें ऑक्सीजन की अपेक्षा 10 लाख गुना कम ऊंचाई पार करना पड़ती है, तो उपरोक्त नियम के मुताबिक इमल्शन के कण का भार ऑक्सीजन के अणु के भार से 10 लाख गुना अधिक होगा।
इस विधि का उपयोग करना आसान है क्योंकि आपको सिर्फ दो चीज़ें नापना है - इमल्शन के कणों का भार और उसमें विरलता को दुगना करने के लिए ऊंचाई।
और अब प्रयोग
पेरिन ने यह प्रयोग सफलतापूर्वक संपन्न किया। सबसे पहले उन्होंने विभिन्न रेज़िन्स के गोलाकार कण बनाए। इसके लिए वे पहले तो रेज़िन। को अल्कोहल में घोल लेते थे और फिर इस घोल को ढेर सारे पानी में डालते थे। रेज़िन पानी में अघुलनशील होने के कारण उसमें लेई-सी बन जाती थी। इस लेई को सेंट्रीफ्यूज करते थे। सेंट्रीफ्यूज करना यानी इसे एक उफननली में रखकर तेज़ गति से घुमाना। यह लगभग वैसा ही होता है जैसा कि दूध में से क्रीम निकालने के लिए किया जाता है। ऐसा करने पर लेई में मौजूद ठोस रेज़िन के कण परखनली की पेंदी में जमा हो जाते हैं और ऊपर साफ तरल बच जाता है। अल्कोहल व पानी के इस मिश्रण को निथार देते हैं तो रेज़िन के कण परखनली में बच जाते हैं।
इसके बाद पेरिन के सामने समस्या थी कि उनके पास रेज़िन के एक ही साइज़ के कण होने चाहिए - तभी तो वे उपरोक्त समीकरण को लागू कर पाते। इसके लिए एक बार फिर इन कणों की लेई बनाई गई और अत्यंत नियंत्रित ढंग से सेंट्रीफ्यूज किया गया। इसमें सबसे मोटे कण सबसे नीचे बैठते हैं और सबसे बारीक कण सबसे ऊपर। यह वैसा ही है जैसे यदि हम मिट्टी को पानी में घोलकर रखा रहने दें तो धीरे-धीरे पेंदे में कण अपने आकार के अनुसार बैठ जाते हैं।
इस तरह कई बार सेंट्रीफ्यूज करने के बाद पेरिन एकरूप कण प्राप्त करने में सफल रहे। वैसे इस प्रक्रिया में काफी धैर्य की ज़रूरत थी। पेरिन अपने नोबल व्याख्यान में बताते हैं कि उन्होंने 1 किलोग्राम गैम्बोगे रेज़िन से शुरु किया था। और कई महीनों के बाद उन्हें चंद डेसिग्राम ऐसे कण मिल पाए थे जिनका व्यास मिलीमीटर के हज़ारवें भाग का भी तीन-चौथाई था। सूक्ष्मदर्शी की मदद से उन्होंने इनका व्यास कैसे नापा, इनसे बनी एक गेंद का घनत्व कैसे नापा, वह एक अलग कहानी है। कुल मिलाकर हम इस पचड़े में नहीं पड़ेंगे कि उन्होंने इन कणों का भार कैसे पता किया।
बहरहाल, कणों का आकार एक-सा है और भार मालूम है तो हम आगे बढ़ सकते हैं।
उनका अगला लक्ष्य यह पता करना था कि यदि इन कणों से बने इमल्शन को गुरुत्व के भरोसे छोड़ दिया जाए तो साम्यावस्था स्थापित होने के बाद ऊंचाई के साथ कणों का वितरण किस तरह बदलता है। इसके लिए उन्होंने एक अत्यंत छोटी-सी तश्तरी में एक बूंद इमल्शन डाला और उसे कवर स्लिप से अच्छी तरह बंद कर दिया ताकि वाष्पन की कोई गुंजाइश न रहे। शुरु में तो कणों का वितरण एक सा रहता है। धीरे-धीरे कण निचली परतों में अधिक जमा होने लगते हैं और ऊपर वाली परतों में उनका घनत्व कम होने लगता है।
कणों के घनत्व के अवलोकन की दो विधियां थीं। एक विधि में आड़े सूक्ष्मदर्शी का उपयोग करते थे और फोटो खींच लेते थे। बाद में इन फोटो से अलग - अलग ऊंचाइयों पर कणों की संख्या ज्ञात कर लेते थे। मगर इसमें एक दिक्कत यह थी कि इस विधि के उपयोग में इमल्शन की कुल ऊंचाई (गहराई) करीब 1 मि.मी. से कम नहीं रखी जा सकती थी और साम्यावस्था बनने में कई दिन लग जाते थे।
दूसरी विधि में सूक्ष्मदर्शी खड़ा होता था। स्लाइड पर रखे इमल्शन और उसे ढंकने वाली कवर स्लिप के बीच की दूरी (यानी इमल्शन की ऊंचाई) 1 मि.मी. के दसवें भाग के बराबर थी। यहां उन्होंने सूक्ष्मदर्शी के एक दिलचस्प गुण का फायदा उठाया था। यदि आपके सूक्ष्मदर्शी के ऑब्जेक्टिव की आवर्धन क्षमता बहुत अधिक है तो उससे एक समय में बहुत ही पतली कटान (करीब 2 माइक्रॉन) फोकस में आती है। इस तरह इमल्शन की अलग-अलग कटानों को फोकस करके उन्होंने विभिन्न ऊंचाई की परतों में कणों की संख्या गिन ली।
अब उनके पास एवोगैड्रो संख्या की गणना के लिए सारे आंकड़े थे। आगे बढ़ने से पहले बता दें कि पेरिन ने एक ऐसा इमल्शन बनाया था जिसमें हर 6 माइक्रॉन पर विरलता दुगनी होती थी। हम जानते ही हैं कि ऑक्सीजन में विरलता हर 5 कि.मी. पर दुगनी होती है। तो ऑक्सीजन का एक अणु इमल्शन के एक कण से लगभग 1 करोड़ गुना कम वज़नदार है। इमल्शन के कण का वज़न पेरिन निकाल ही चुके थे, तो ऑक्सीजन या किसी भी गैस के अणु का वज़न निकालने में कितनी देर लगनी थी। इसके आधार पर बताया जा सकता है कि 1 ग्राम गैस में कितने अणु हैं। यानी यह भी निकाला जा सकता है कि 1 मोल गैस में कितने अणु हैं।
इसके आधार पर गणना करने पर एवोगैड्रो संख्या का मान 68x1022 आया। यह वर्तमान में मान्य संख्या (6.0221415 ± 0.0000010) x 1023 के काफी करीब है। पेरिन ने एवोगैड्रो संख्या ज्ञात करने का प्रयोग कई तरह से किया था। जैसे उन्होंने रेज़िन के कणों का भार बदलकर देखा (1 इकाई से 50 इकाई तक), उनकी प्रकृति बदलकर देखी (गैम्बोगे से लेकर मैस्टिक तक), उनका आपेक्षिक घनत्व बदला (1.20 से 1.06), विलायक बदलकर देखा (पानी, शक्कर की चाशनी, ग्लिसरीन) और अलग-अलग तापमान (-90 से +600 तक) पर प्रयोग करके देखे।
वैसे पेरिन ने ये प्रयोग उन्नीसवीं सदी के अंत और बीसवीं सदी की शुरुआत में किए थे और उस समय तो पदार्थों की कण प्रकृति को ही स्थापित करने की मशक्कत चल रही थी। इसलिए पेरिन को नोबल पुरस्कार एवोगैड्रो संख्या ज्ञात करने के लिए नहीं बल्कि कण प्रकृति को निर्विवाद रूप से स्थापित करने के लिए दिया गया था।
पेरिन के इस व्यापकतर लक्ष्य का तकाज़ा था कि अलग-अलग कई प्रयोगों के अवलोकनों की व्याख्या कण प्रकृति से की जाए जिसके मद्देनज़र उन्होंने इतने सारे तरीके अपनाए।
सुशील जोशी: एकलव्य द्वारा प्रकाशित स्रोत फीचर सेवा से जुड़े हैं। विज्ञान लेखन में रुचि।
