एवोगैड्रो संख्या कुछ और विधियां

सुशील जोशी

भाग:3
पिछले अंक में हमने एवोगैड्रो संख्या ज्ञात करने की पेरिन विधि की बात की थी। मैं आपको याद दिला दूं कि एवोगैड्रो संख्या अणु, परमाणु की वह संख्या है जो उस पदार्थ के एक मोल में पाई जाती है। वर्तमान में इसका मान 6.02296 (+/- 0.00017) x 10²³ माना जाता है। मैंने कहा था कि अगले अंक में इसी संख्या को ज्ञात करने की कुछ और विधियों की बात करूंगा।

यह आश्चर्य का विषय है कि इस संख्या को प्रायोगिक रूप से ज्ञात करने के एक दर्ज़न से ज़्यादा प्रयास किए गए हैं। मगर इसमें इतना आश्चर्य नहीं होना चाहिए क्योंकि पदार्थ की परमाणु प्रकृति का प्रमुख प्रमाण यह है कि हम परमाणुओं, अणुओं वगैरह को गिन सकते हैं और विभिन्न विधियों से गिनने पर लगभग एक जैसा मान प्राप्त होता है।
इस बार मैं विधियों के विस्तार में नहीं जाऊंगा। मैं करूंगा यह कि उनका मोटा-मोटा सिद्धांत बताऊंगा, प्रायोगिक बारीकियां छोड़ दूंगा। इसलिए शायद ये विधियां अत्यंत सरल जान पड़ें मगर याद रखें कि इनमें से कई विधियों के लिए बरसों तक प्रयोग किए गए थे और कई प्रायोगिक गुत्थियां सुलझानी पड़ी थीं।
सबसे पहले देखते हैं रदरफोर्ड और गाइगर द्वारा विकसित विधि।

रदरफोर्ड-गाइगर विधि
इस विधि का आधार यह है कि रेडियम नामक तत्व में विखंडन होता रहता है यानी उसके परमाणु टूटते रहते हैं। विखंडन के दौरान रेडियम में से एक निश्चित संख्या में अल्फा कण निकलते रहते हैं। ये अल्फा कण और कुछ नहीं, हीलियम के नाभिक होते हैं। यदि इन्हें इलेक्ट्रॉन मिल जाए तो ये हीलियम के परमाणु बना लेते हैं। अल्फा कणों की संख्या मात्र इस बात पर निर्भर करती है कि आपने कितना रेडियम लिया है। आप रेडियम की एक निश्चित मात्रा लेकर उसमें से एक निश्चित समय में उपजी हीलियम को नाप सकते हैं - आयतन और भार। यह इस विधि का पहला भाग है।

दूसरा भाग यह है कि रेडियम से निकले अल्फा कण जब ज़िंक सल्फाइड के पर्दे से टकराते हैं तो पर्दे पर चमक पैदा होती है। इस तरह से एक निश्चित समय में निकले अल्फा कणों की मात्रा गिनी जा सकती है। इसके लिए जिस उपकरण का उपयोग किया जाता है उसे स्पिंथेरिस्कोप कहते हैं।
करते यह हैं कि रेडियम का एक छोटा-सा नमूना लेकर उसे ज़िंक सल्फाइड के पर्दे के सामने रख देते हैं और एक दूरबीन में से देखकर गिनते रहते हैं कि कितने अल्फा कण निकले।

प्रथम भाग के आधार पर आप यह गणना करते हैं कि यदि एक निश्चित मात्रा में रेडियम लिया जाए, तो एक निश्चित समय में कितनी हीलियम (घन से.मी. में) बनेगी। इसके लिए आपके पास प्रायोगिक रूप से प्रतिपादित सूत्र हैं। द्वितीय भाग से आप यह जानते हैं कि उतने ही समय में कितने अल्फा कण निकलते हैं जो हीलियम परमाणुओं में तब्दील हो जाते हैं। यानी आप पता कर सकते हैं कि ये कण कितने घन से.मी. हीलियम में हैं। इसके आधार पर आप यह गणना कर सकते हैं कि 22,414 घन से.मी. (सामान्य ताप और दाब पर एक मोल हीलियम या किसी गैस का आयतन) में कितने परमाणु होंगे। शुरु में इस विधि से निम्नलिखित मान प्राप्त हुए थे:

प्रति घन से.मी. में अणुओं की संख्या
= 2.7 x 10¹⁹
एवोगैड्रो संख्या = 6.05 x 10²³
प्रसंगवश बता दूं कि एक घन से.मी. गैस में उपस्थित अणु या परमाणुओं की संख्या को लॉश्मिट संख्या भी कहते हैं।
आगे चलकर सन् 1908 में इस विधि के उपकरण में सुधार किया गया और अल्फा कणों को गिनने के लिए इन कणों को कम दबाव पर रखी एक गैस में भेजा गया। ये कण गैस को आयनीकृत कर देते थे। हर बार आयनीकरण होने पर धारा प्रवाहित होती थी। अत: इन कणों को गिना जा सकता था। इस नए तरीके से एवोगैड्रो संख्या का मान 6.14 x 10²³ निकला।

मिलिकन की विधि
मिलिकन की विधि वास्तव में आठ सालों तक किए गए प्रयोगों का परिणाम थी और ये प्रयास वास्तव में एवोगैड्रो संख्या ज्ञात करने के लिए नहीं किए गए थे। मिलिकन का प्रयास एक इलेक्ट्रॉन पर उपस्थित आवेश की मात्रा ज्ञात करने का था। मगर उनके परिणामों को जब फैरेडे द्वारा किए गए प्रयोगों के परिणामों के साथ जोड़कर देखा गया तो एवोगैड्रो संख्या का मान प्राप्त हुआ।
चूंकि फैरेडे के प्रयोग काफी पहले हो चुके थे, इसलिए पहले उनका ज़िक्र मुनासिब है। विद्युत अपघटन संबंधी अपने प्रयोगों से फैरेडे सन् 1834 में दर्शा चुके थे कि विभिन्न आयनिक पदार्थों के घोलों में से बराबर मात्रा में बिजली प्रवाहित करने पर बराबर मात्रा में अपघटन होता है। अपघटन से प्राप्त तत्व की मात्रा उसके तुल्यांक भार के समानुपाती होती है। जैसे यदि कॉपर सल्फेट, सिल्वर नाइट्रेट और लेड नाइट्रेट के घोलों में बराबर धारा प्रवाहित की जाए, तो कैथोड पर जमा हुए तांबे, चांदी और सीसे की मात्रा 31.785 : 107.88 : 103.61 के अनुपात में होती है।

इस नियम का मतलब यह होता है कि एक ग्राम तुल्यांक भार के बराबर कोई भी तत्व जमा करने के लिए विद्युत की मात्रा बराबर होगी - यह मात्रा 96,500 कूलंब पाई गई थी (जिसे 1 फैरेडे कहते हैं)। यह मान सबसे पहले फैरेडे ने नहीं बल्कि 1912 में वॉशबर्न और बेट्स ने ज्ञात किया था।

फैरेडे के प्रयोगों का एक महत्वपूर्ण पक्ष तत्काल उजागर नहीं हुआ था। वैसे तो उसकाहमारी चर्चा से संबंध नहीं है मगर उसका ज़िक्र गैर मुनासिब न होगा। इस पक्ष को हेल्महोल्ट्ज़ ने सन् 1881 में रॉयल सोसायटी के समक्ष दिए गए अपने फैरेडे व्याख्यान में उजागर किया था: “फैरेडे के नियमों का सबसे हैरतअंगेज़ परिणाम यह है। यदि हम मानते हैं कि प्राथमिक पदार्थ परमाणुओं से बने हैं, तो हम यह निष्कर्ष निकालने से बच नहीं सकते कि विद्युत भी निश्चित हिस्सों में बंटी होती है जो विद्युत के परमाणुओं की तरह व्यवहार करते हैं।” इसी में से इलेक्ट्रॉन (विद्युत का परमाणु) का विचार उभरा था। विद्युत की इस निश्चित मात्रा को इलेक्ट्रॉन का नाम जी. जॉनस्टन स्टोनी ने दिया था।

खैर अपने विषय पर लौटें। फैरेडे के नियम से हम जानते हैं कि किसी तत्व का 1 ग्राम तुल्यांक जमा करने के लिए 96,500 कूलंब विद्युत की ज़रूरत होती है। यानी यदि एक आवेश वाले आयन जमा हो रहे हैं, तो तुल्यांक भार और अणु भार बराबर होगा। अर्थात 96,500 कूलंब से एक मोल तत्व जमा हो जाएगा। इसका यह भी मतलब है कि 96,500 कूलंब एक मोल इलेक्ट्रॉन के बराबर है। अब यदि आपको एक इलेक्ट्रॉन का आवेश मालूम हो, तो आप एक मोल में इलेक्ट्रॉन की संख्या निकाल सकते हैं।

रॉबर्ट मिलिकन ने इलेक्ट्रॉन का आवेश निकालने का जुगाड़ किया था और इसमें उन्हें पूरे आठ साल तक प्रयोग करने पड़े थे। उन्होंने दरअसल टाउनसेण्ड नामक वैज्ञानिक की विधि में सुधार ही किया था मगर इस विधि को मिलिकन की विधि ही कहते हैं।

इस विधि में किसी तेल की बहुत बारीक फुहार तैयार की जाती है। इस फुहार को दो प्लेट्स के बीच भेजा जाता है जहां एक्स किरणों की बौछार होती रहती है और तेल की बारीक-बारीक बूंदें घर्षण के कारण धनात्मक आवेशित हो जाती हैं। यदि न भी हो पाई हों, तो एक्स किरणें इन्हें आवेशित कर देती हैं। दो प्लेटों के बीच उच्च विभव आरोपित किया जा सकता है और बदला जा सकता है।

प्रयोग इस तरह किया जाता था कि पहले बूंद को गुरुत्व के प्रभाव से गिरने देते थे। जब वह लगभग निचली प्लेट के पास पहुंचने को होती, तब विभव आरोपित किया जाता ताकि वह फिर से ऊपर चली जाए। हर बार जब कोई बूंद आवेश ग्रहण करती तो उसके ऊपर उठने के वेग में परिवर्तन से पता चल जाता था कि ऐसा हुआ। नीचे गिरने का वेग तो स्थिर रहता था।

मिलिकन के प्रयोगों से पता चला था कि हर बार एक अतिरिक्त आवेश पकड़ने पर बूंद के उर्ध्व वेग में लगभग बराबर परिवर्तन होता है जो औसतन 0.00891 से.मी. प्रति सेकंड था। हर बार एक आवेश के कारण वेग में बराबर परिवर्तन का मतलब था कि हर बार जो आवेश बूंद पर आता है उसकी मात्रा बराबर है। इस मान के आधार पर इलेक्ट्रॉन के लिए आवेश/संहति का मान तो निकाला जा सकता था। यदि संहति मालूम हो, तो आवेश की मात्रा पता लग सकती है।

बूंदों के नीचे गिरने के वेग को लेकर स्टोक्स ने कई प्रयोग करके कुछ नियम व समीकरणें विकसित की थीं। कुल मिलाकर ये समीकरणें बताती हैं कि इतनी बारीक बूंदों के गिरने पर गुरुत्व बल के अलावा हवा के उछाल बल व घर्षण बल का भी असर पड़ता है जो बूंदों की साइज़, संहति, माध्यम के घनत्व तथा श्यानता पर निर्भर करता है। उनके समीकरण से बूंदों के वेग के आधार पर उनकी संहति ज्ञात की जा सकती है। मिलिकन ने बूंदों की संहति ज्ञात करने के लिए स्टोक्स के थोड़े सुधरे हुए रूप का उपयोग किया था।

इस तरह गणना करने पर इलेक्ट्रॉन पर आवेश की मात्रा 1.602 X 10^-17 कूलंब निकली। फैरेडे के प्रयोगों से यह तो पता ही था कि एक मोल इलेक्ट्रॉन का आवेश 96,500 कूलंब होता है। तो एक मोल में इलेक्ट्रॉन की संख्या निकालना गणित का खेल ही बच गया था।

आप देख ही सकते हैं कि विधि काफी मुश्किल है और यकीन मानिए, इन प्रयोगों को करना इससे कहीं अधिक मुश्किल रहा होगा। हम चलते हैं अगली विधि पर। यह विधि एक्स किरणों और परमाणुओं की परस्पर क्रिया पर आधारित है और माना जाता है कि सबसे विश्वसनीय आंकड़ा देती है।

एक्स किरण विधि
इस विधि का मूल यह है कि एक्स किरणें जब किसी रवेदार यानी क्रिस्टेलाइन पदार्थ पर डाली जाती हैं तो वे विवर्तित (diffract) हो जाती हैं। यह तो आप जानते ही होंगे कि प्रत्येक पदार्थ की एक विशिष्ट क्रिस्टल संरचना होती है। जब किसी क्रिस्टल पर एक्स किरण डाली जाती है और दूसरी तरफ एक फोटोग्राफी प्लेट रखी जाती है तो उस पर बिंदुओं का एक पैटर्न प्राप्त होता है। ये बिंदु मोटे तौर पर क्रिस्टल में परमाणुओं की स्थिति दर्शाते हैं। इसके आधार पर, दिए गए क्रिस्टल में आप परमाणुओं की दूरी पता कर सकते हैं। क्रिस्टल दरअसल परमाणुओं के बारंबार दोहराए जाने वाले पैटर्न से बने होते हैं। ऐसे पैटर्न की एक इकाई को हम एक सेल कहते हैं।

एक्स किरण विवर्तन की मदद से हम यह पता लगा सकते हैं कि किसी क्रिस्टल की एक सेल कितनी बड़ी है और इस एक सेल में कितने परमाणु हैं। इसके आधार पर यह पता लगाना मुश्किल नहीं है कि उस पदार्थ के एक मोल में कितनी सेल होंगी और कुल कितने परमाणु होंगे। एक उदाहरण से बात को समझते हैं।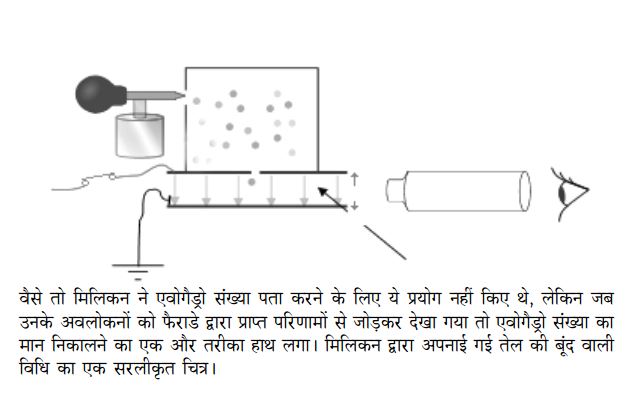

जैसे सोडियम क्लोराइड को ही लेते हैं। रवेदार नमक का घनत्व 2.169 ग्राम प्रति घन से.मी. है। इसका अणु भार 58.45 है। एक्स किरण विवर्तन से पता चलता है कि इसकी क्रिस्टल संरचना अगले पृष्ठ पर दिए गए चित्र जैसी होती है। इसमें बड़े काले गोले सोडियम तथा छोटे सफेदे गोले क्लोरीन के परमाणु के द्योतक हैं। चित्र में सोडियम क्लोराइड क्रिस्टल के चार सेल दिखाए गए हैं।

यहां एक बात पर ध्यान दें कि हालांकि चित्र में सोडियम के 14 परमाणु दिख रहे हैं मगर वे पड़ोसी सेलों के भी हिस्से हैं, जिस वजह से उन्हें दो बार, चार बार गिनने से बचना होता है। इसलिए प्रत्येक परमाणु को किसी एक सेल को आवंटित कर दिया जाता है। जैसे कोने वाले 8 सोडियम परमाणुओं को लें। इनमें से प्रत्येक 8 सेलों का हिस्सा है। अत: इनमें से प्रत्येक का 1/8 हिस्सा एक सेल को आवंटित होगा - यानी इनमें से कुल 1 सोडियम परमाणु इस सेल का अंग है। अब फलक पर उपस्थित सोडियम परमाणुओं को देखें। ऐसे 6 परमाणु हैं। प्रत्येक दो-दो सेलों का हिस्सा है इसलिए प्रत्येक का आधा यानी कुल तीन इस सेल को मिलेंगे। इसी प्रकार कुल 4 सोडियम परमाणु इस सेल में हैं। इस चित्र में चार सेल दिख रही हैं जिनमें सोडियम के चार और क्लोरीन के चार परमाणु हैं। अत: प्रत्येक सेल में 1-1 सोडियम व क्लोरीन परमाणु होगा।

एक्स किरण विवर्तन से पता चलता है कि इस क्रिस्टल में एक सोडियम परमाणु से दूसरे की दूरी 5.65 आंगस्ट्रॉम है। तो चार सेलों का आयतन होता है 5.653 आंग्रस्ट्रॉम3 = 179.1 आंगस्ट्रॉम3। एक सेल का आयतन हुआ 44.8 आंगस्ट्रॉम3। घन से.मी. इकाई में यह आयतन होगा 44.8 x 10^-24 से.मी.3।

प्रति मोल भार है 58.45 ग्राम।
घनत्व है 2.169 ग्राम प्रति घन से.मी.।
घनत्व = मोल भार/(आयतन x एवोगैड्रो संख्या)
घनत्व (2.169 ग्राम प्रति से.मी.3) = 58.45 ग्राम/(44.8 x10-24 से.मी.3 x N)
जहां N एवोगैड्रो संख्या है। तो
N = 58.45 ग्राम/(44.8 x 10-24 से.मी.3 x 2.169)
= 6.023x10²³
तो इसके साथ हम एवोगैड्रो संख्या कथा बंद करते हैं मगर उससे पहले एक ऐसी विधि का ब्यौरा मौजूं होगा जिसे आप भी आज़मा सकते हैं।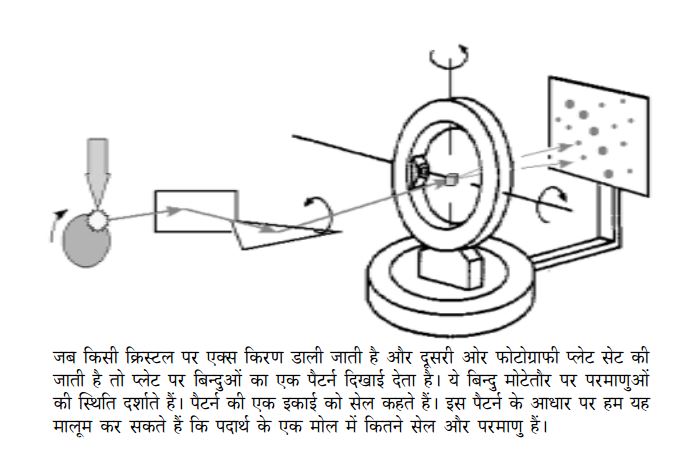

घरेलू विधि
यह विधि उतनी घरेलू भी नहीं है मगर काफी सरल है और ऐसे उपकरणों व सामग्री से की जा सकती है जो किसी भी हायर सेकंडरी स्कूल की प्रयोगशाला में उपलब्ध होंगे।
विधि का मूल सिद्धांत यह है कि आप मानकर चलते हैं कि अणु घनाकार होते हैं। दूसरी बात आप यह मानकर चलते हैं कि यदि किसी जलस्नेही (हाइड्रोफिलिक पदार्थ) को पानी पर फैलने दिया जाए तो वह अधिकतम फैलेगा और अंतत: एक ऐसी झिल्ली के रूप में फैल जाएगा जिसकी मोटाई एक अणु के बराबर होगी।
इस विधि से एवोगैड्रो संख्या पता करने के लिए हमें निम्नलिखित पदार्थों की ज़रूरत होगी: एक प्लास्टिक का टब, पानी, पिस्टन ऑइल, रासायनिक तुला, एक आयतन मापी फ्लास्क, ओलीक अम्ल, हेक्सेन, पारदर्शी कागज़, ग्राफ कागज़, पेंसिल।

तरीका निम्नानुसार है:
1. 10 मि.ग्रा. ओलीक अम्ल को 100 मिली लीटर हेक्सेन में घोल लें।
2. प्लास्टिक के टब में पानी भरकर उस पर थोड़ा-सा पिस्टन ऑइल डाल दें।
3. ओलीक अम्ल के घोल में से 50 माइक्रोलीटर मात्रा इस पानी पर डालें। यदि आपके पास माइक्रो-पिपेट न हो, तो सिरिंज का उपयोग करें। यदि सिरिंज पर आपने 22 गेज की सुई लगाई है, तो इससे 6 बूंद घोल डालें। यदि सुई 24 गेज की है तो 9 बूंद घोल डालना होगा।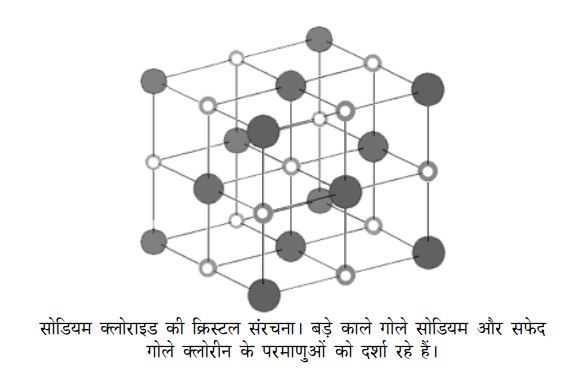
4. हेक्सेन तुरंत उड़ जाएगा और ओलीक अम्ल पिस्टन ऑइल को धकेलते हुए एक पतली झिल्ली के रूप में फैल जाएगा। टब के ऊपर एक पारदर्शी कागज़ को इस झिल्ली से थोड़ा ऊपर रखकर झिल्ली की रेखाकृति खींच लीजिए।
5. इस पारदर्शी कागज़ को एक ग्राफ कागज़ पर रखकर क्षेत्रफल ज्ञात कर लें।

हमने माना है कि यह झिल्ली एक अणु मोटी है। अत: इसकी मोटाई ओलीक अम्ल के एक अणु की मोटाई है। हमने यह भी माना है कि अणु घनाकार हैं। अत:अणु की मोटाई के आधार पर एक अणु के आयतन की गणना की जा सकती है।

एक अणु का आयतन पता हो गया और उस झिल्ली में ओलीक अम्ल का कुल आयतन पता ही है। अब उस झिल्ली में अणुओं की कुल संख्या निकाल लीजिए।
इतने अणु 0.00005 ग्राम ओलीक अम्ल में हैं, तो आपके लिए यह गणना कदापि मुश्किल न होगी कि एक मोल (282 ग्राम) ओलीक अम्ल में कितने अणु होंगे।

सुशील जोशी: एकलव्य द्वारा प्रकाशित स्रोत फीचर सेवा से जुड़े हैं। विज्ञान लेखन में रुचि।