आइज़ेक एसीमोव
अनुवाद: रमा चारी
भाग-2
इन विज्ञान निबन्धों के लेखन में मग्न हो जाने से कई बार मुझे परेशानियों का सामना करना पड़ता है। एक बार मैं अपने एक मित्र के साथ खाना खा रहा था। उन्होंने पहला कौर चखने के बाद खाने पर नमक छिड़का और फिर दूसरा कौर चखकर कहा, “अब ज़्यादा अच्छा है।” मैं थोड़ा कुनमुनाया, फिर उनसे कहा, “असल में आपको कहना चाहिए कि अब मुझे ज़्यादा अच्छा लगा।” जब आप सिर्फ “अब ज़्यादा अच्छा है” कहते हैं तब आप एक अनुचित व अवांछित पूर्वानुमान लगा रहे हैं कि कोई भी भोजन वस्तुनिष्ठ रूप से (objectively) स्वादिष्ट या बेस्वाद हो सकता है और यह भी कि आपका स्वाद का वैयक्तिक (subjective) निर्णय वस्तुनिष्ठ हो सकता है। अर्थात् ज़रूरी नहीं कि जो चीज़ आपको स्वादिष्ट लगे वही दूसरे को भी अच्छी लगे।
मेरा ख्याल है कि यह सुनकर मित्र की इच्छा मेरे मुँह पर थाली उठाकर मार देने की हुई होगी और इसमें कुछ गलत भी नहीं होता। दरअसल, मैंने पहले वाला लेख अभी लिखा ही था और ‘मान्यताएँ’ मेरे दिमाग पर पूरी तरह छाई हुई थीं।
चलिए, वापस यूक्लिड के पाँचवें आधार तत्व को देखते हैं, जो कुछ इस प्रकार है:
“यदि एक सरल रेखा, दो अन्य सरल रेखाओं को इस प्रकार काटती है कि कटाव के एक तरफ के अन्त:कोणों का योग दो समकोणों के योग से कम हो तो वे दो सरल रेखाएँ अनन्त तक बढ़ाई जाने पर उसी तरफ आपस में मिलेंगी जिस तरफ के समकोणों का योग दो समकोणों से कम हो।”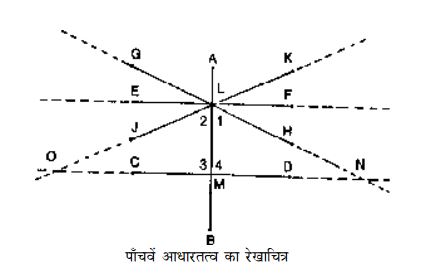
यूक्लिड के बाकी नौ स्वसिद्ध काफी सरल हैं। परन्तु यूक्लिड शायद यह समझ गए थे कि पाँचवाँ आधारतत्व चाहे कितना भी दुरूह लगे, उसे बाकी नौ स्वसिद्धों से सिद्ध नहीं किया जा सकता और उसे एक स्वसिद्ध ही मानना पड़ेगा।
यूक्लिड के बाद दो हज़ार साल तक अन्य रेखाशास्त्री यह दिखाने की कोशिश करते रहे कि यूक्लिड ने थोड़ी जल्दबाज़ी की। उनका प्रयत्न इस ओर रहा कि वे किसी तरह पाँचवें आधारतत्व को बाकी नौ स्वसिद्धों के द्वारा सिद्ध कर लें। अगर ऐसा हो पाता तो इस लम्बे और दुरूह कथन को स्वसिद्ध सूची से हटाया जा सकता था।
इस बात को सिद्ध करने का एक तरीका इस प्रकार था। सामने पृष्ठ पर दिए चित्र में दर्शित चतुर्भुज को देखें। इसमें दिया हुआ है कि दो कोण DAB और ABC समकोण हैं और भुजा AD लम्बाई में भुजा BC के बराबर है। इन दिए गए तथ्यों के आधार पर यह सिद्ध किया जा सकता है कि भुजाएँ DC और AB भी आपस में बराबर होंगी और कोण ADC व DCB भी समकोण होंगे अर्थात् यह चतुर्भुज वास्तव में एक आयत होगा। लेकिन यह सिद्ध करना तभी सम्भव है जब यूक्लिड के पाँचवें आधारतत्व का उपयोग किया जाए। इसका उपयोग किए बिना अर्थात् केवल बाकी नौ स्वसिद्धों का उपयोग करके केवल इतना सिद्ध किया जा सकता है कि कोण ADC व DCB आपस में बराबर होंगे; यह नहीं कि ये कोण समकोण भी होंगे।
अब प्रश्न यह उठता है कि क्या ADC और DCB कोणों के बराबर होने से यह सिद्ध किया जा सकता है कि वे समकोण भी होंगे? अगर ऐसा किया जा सके तो सिद्ध हो जाएगा कि चतुर्भुज ABCD वास्तव में एक आयत है और पाँचवें आधारतत्व को बाकी स्वसिद्धों का उपयोग करके सिद्ध किया जा सकेगा और फिर उसे यूक्लिड की स्वसिद्ध सूची में रखने की कोई आवश्यकता नहीं होगी।
अरबों की पहल
इस प्रकार का प्रयत्न सबसे पहले मध्ययुगीन अरबों ने किया था, जिन्होंने उस समय यूनानी ज्यामिति की परम्परा को आगे बढ़ाया ,जब पश्चिमी यूरोप अज्ञान के अँधेरे में डूबा हुआ था। चित्र में दिए चतुर्भुज और उसके समकोणों का विवेचन सर्वप्रथम उमर खैय्याम (1050-1123) ने किया था।
उमर खैय्याम ने कहा कि यदि दोनों कोण ADC और DCB बराबर हैं तो तीन सम्भावनाएँ हो सकती हैं: एक - दोनों कोण समकोण हैं। दूसरी - दोनों कोण समकोण से छोटे हैं अर्थात न्यूनकोण हैं। तीसरी - दोनों कोण समकोण से बड़े हैं अर्थात् अधिक कोण हैं। फिर उन्होंने तर्क द्वारा यह सिद्ध किया कि पहली दो सम्भावनाएँ, इस मान्यता के आधार पर कि दो अभिमुखी (converging) रेखाएँ एक-दूसरे को अवश्य काटेंगी, बेतुकी हैं।
अब यह तो ज़ाहिर लगता है कि दो अभिमुखी रेखाएँ एक-दूसरे को काटेंगी ही, पर दुर्भाग्य से यह मान्यता वास्तव में यूक्लिड के पाँचवें आधारतत्व के समतुल्य है। अर्थात् उमर खैय्याम ने पाँचवें आधारतत्व का आधार लेकर पुन: उसे ‘सिद्ध’ किया। इसे हम ‘हाथ की सफाई’ कह सकते हैं, पर यह गणित शास्त्र में मान्य नहीं हो सकता।
एक और अरबी गणितज्ञ नसीरुद्दीन अल्तस (1201-74) ने भी एक चतुर्भुज को लेकर ऐसा ही एक और प्रयत्न किया। उन्होंने एक अन्य व अधिक दुरूह मान्यता प्रारम्भ कर अधिक व न्यून कोण वाली सम्भावनाओं को गलत सिद्ध किया। पर फिर वही बात, उनकी उपयोग की हुई मान्यता भी गणितीय दृष्टि से यूक्लिड के पाँचवें आधारतत्व के समतुल्य थी।
सच्चेरी और न्यूनकोण ज्यामिति
इसके बाद हम पहुँचते हैं इतालवी गणितज्ञ जिरोलामो सच्चेरी (1667-1733) तक जिनकी चर्चा मैंने पहले लेख में की थी। वे पीसा विश्वविद्यालय में गणित के प्राध्यापक होने के साथ-साथ जेसुइट धर्मगु डिग्री भी थे। वे नसीरुद्दीन के काम के बारे में जानते थे। उन्होंने भी इस चतुर्भुज की समस्या से जूझना शुरु किया। लेकिन सच्चेरी ने एक ऐसी युक्ति अपनाई जो कि यूक्लिड के पाँचवें आधारतत्व के बारे में इन दो हज़ार वर्षों में किसी को भी नहीं सूझी थी।
उस समय तक सबने दो तरह से इस समस्या का हल ढूँढ़ने का प्रयत्न किया था - या तो उन्होंने यह देखा था कि यदि पाँचवें आधारतत्व को छोड़ दिया जाए तो क्या होगा या फिर पाँचवें आधारतत्व के स्थान पर कोई अन्य मान्यता अपनाई जो अन्त में यूक्लिड के पाँचवें आधारतत्व के समतुल्य ही निकली। इसके विपरीत सच्चेरी ने शुरुआत ही इससे की कि यूक्लिड का पाँचवाँ आधारतत्व असत्य है। उसके स्थान पर उन्होंने कोई और आधारतत्व मान्यता अपनाई जो पाँचवें आधारतत्व के विपरीत थी। उनका उद्देश्य था कि यूक्लिड के बाकी स्वसिद्ध और इस मान्यता को लेकर ज्यामिति का विकास तब तक करें जब तक वे किसी विरोधाभास पर न पहुँच जाएँ (विरोधाभास का एक उदाहरण यह होगा कि किसी भी प्रमेय को अलग-अलग तरीके से सत्य और असत्य दोनों सिद्ध कर पाना)।
उनका सोचना था कि जब इस प्रकार का विरोधाभास मिलेगा तो उन्हें नए वाले पाँचवें आधारतत्व को सूची में से हटाना पड़ेगा। अगर प्रत्येक सम्भव वैकल्पिक पाँचवें आधारतत्व को इस तरह हटाया जा सके तो इससे सिद्ध हो जाएगा कि यूक्लिड का पाँचवाँ आधारतत्व सत्य और आवश्यक है। किसी भी तथ्य को सिद्ध करने का यह तरीका गणित में स्वीकार्य है, अत: सच्चेरी सही रास्ते पर थे।
इस पद्धति का उपयोग करते हुए सच्चेरी ने इस ऊपर दी हुई तीसरी सम्भावना को लिया अर्थात् यह मानकर शुरुआत की कि कोण ADC और DCB दोनों समकोण से बड़े हैं। इस मान्यता के साथ बाकी नौ स्वसिद्धों को लेकर उन्होंने अधिक-कोण ज्यामिति विकसित करनी शु डिग्री की। जल्दी ही वे एक विरोधाभास पर पहुँच गए। इसका मतलब यह हुआ कि अधिक-कोण ज्यामिति सही नहीं हो सकती और कोण ADC व DCB समकोण से बड़े नहीं हो सकते।
सच्चेरी की यह प्राप्ति इतनी महत्वपूर्ण थी कि उमर खैय्याम के उस चतुर्भुज को अब ‘सच्चेरी चतुर्भुज’ कहा जाता है। अपनी इस सफलता से प्रसन्न होकर सच्चेरी ने अब ‘न्यूनकोण ज्यामिति’ की तरफ रुख किया। इस बार उन्होंने यह माना कि दोनों कोण ADC व DCB समकोण से छोटे हैं अर्थात् न्यूनकोण हैं। उन्होंने बड़े हल्के मन से शुरुआत की होगी क्योंकि उन्हें विश्वास रहा होगा कि इस बार भी उन्हें जल्दी ही कोई विरोधाभास मिल जाएगा। अगर ऐसा हुआ तो इसका अर्थ होगा कि यूक्लिड का पाँचवाँ आधारतत्व सिद्ध हो सकता है और उसे स्वसिद्ध सूची में रखने की कोई आवश्यकता नहीं है।
लेकिन जैसे-जैसे सच्चेरी अपनी इस न्यूनकोण ज्यामिति में एक के बाद एक प्रमेय की ओर बढ़ने लगे, उनकी प्रसन्नता व्यग्रता में बदलने लगी क्योंकि उन्हें कोई विरोधाभास नहीं मिल रहा था। उन्हें यह सम्भावना नज़र आने लगी कि यूक्लिड के पाँचवें आधारतत्व के विपरीत स्वसिद्ध को लेकर भी बाकी नौ स्वसिद्धों के साथ एक स्वसंगत (self-consistent)ज्यामिति की रचना की जा सकती है। अगर ऐसा हुआ तो इसका फल होगा एक ऐसी गैर-यूक्लिडीय (non-Euclidean) ज्यामिति जो हमारे सहज ज्ञान से तो बिलकुल उल्टी होगी पर अपने आपमें पूर्णतया स्वसंगत और गणितीय दृष्टि से मान्य होगी।
एक पल के लिए सच्चेरी गणित में अमरत्व पाने की स्थिति में थे, किन्तु उन्होंने हाथ खींच लिया। उनसे यह नहीं हुआ। एक गैर-यूक्लिडीय ज्यामिति की परिकल्पना को स्वीकार करने के लिए बड़े साहस की ज़रूरत थी। उस समय के विद्वान इस भ्रामक स्थिति में थे कि वे यूक्लिड की ज्यामिति को परम सत्य मानते थे। अत: यूक्लिड की किसी भी बात को गलत ठहराना यूरोप के बुद्धिजीवियों के दिलो-दिमाग को घोर परेशानी में डालने वाली बात होती। यूक्लिड पर सन्देह करना यानी परम सत्य पर सन्देह करना। और अगर यह कहा जाए कि यूक्लिड के सिद्धान्त परम सत्य नहीं हैं तो शायद यह भी कहा जा सकता है कि परम सत्य कुछ होता ही नहीं। क्योंकि परम सत्य के होने का सबसे ठोस आधार धर्म था, क्या यूक्लिड के सिद्धान्तों को असत्य ठहराना ईश्वर की सम्भावना पर प्रहार करने जैसा नहीं होगा?
इसमें कोई शक नहीं कि सच्चेरी एक महान सम्भावना वाले गणितज्ञ थे पर साथ ही वे एक ईसाई धर्मगुरु और एक साधारण मनुष्य भी थे, इसलिए वे यह बात कहने की हिम्मत नहीं जुटा पाए और उन्होंने इस बात को नकार दिया। जब उनकी न्यूनकोण ज्यामिति धीरे-धीरे इस बिन्दु पर पहुँच गई कि उससे आगे बढ़ने का साहस उनमें नहीं रहा तब उन्होंने अपने आपको झूठा दिलासा देते हुए एक ऐसे विरोधाभास को खोज लिया जो वास्तव में विरोधाभास था ही नहीं। इस तरह उन्होंने यह (गलत) परिणाम निकाल लिया कि उन्होंने यूक्लिड के पाँचवें आधारतत्व को ‘सिद्ध’ कर लिया है। सन् 1733 में उन्होंने अपने परिणाम एक पुस्तक रूप में प्रकाशित किए। पुस्तक का नाम था, ‘Euclid cleared of Every flaw (यूक्लिड सारे दोषों से मुक्त)। उसी वर्ष उनका देहान्त हो गया।
अपनी ही न्यूनकोण ज्यामिति को नकारने से सच्चेरी ने गणित में अमरत्व पाने का अवसर खो दिया और गुमनामी के अँधेरे में डूब गए। उनकी पुस्तक पर तब तक किसी ने विशेष ध्यान नहीं दिया जब तक एक और इतालवी गणितज्ञ यूजिनियो बेल्ट्रामी (1835-1900) ने उसकी ओर फिर से ध्यान आकर्षित नहीं किया। तब तक सच्चेरी की असफलता पर औरों ने कामयाबी हासिल कर ली थी। इस समय हमें सच्चेरी के बारे में इतना ही पता है कि वे एक अत्यन्त महत्वपूर्ण गणितीय खोज की कगार पर थे, पर अपनी ही खोज पर विश्वास करने का साहस नहीं जुटा पाए।
अब हम करीब सौ साल आगे चलते हैं, जर्मन गणितज्ञ कार्ल गॉस (1775-1855) की तरफ। इसमें कोई सन्देह नहीं कि गॉस अब तक के सबसे महान गणितज्ञ रहे हैं। बहुत ही कम उम्र में उन्होंने यूरोप के वैज्ञानिकों को अपनी बुद्धिमत्ता से चकित कर दिया था।
उन्होंने सन् 1815 के करीब यूक्लिड के पाँचवें आधारतत्व पर काम करना शुरु किया। वे भी यूक्लिड के ही निष्कर्ष पर पहुँचे कि पाँचवें आधारतत्व को बाकी नौ स्वसिद्धों से सिद्ध नहीं किया जा सकता। अत: उसे स्वसिद्ध सूची में शामिल करना ज़रूरी था। लेकिन इससे आगे उन्हें यह भी समझ में आया कि अन्य स्वसंगत (self-consistent) गैर-यूक्लिडीय ज्यामिति भी सम्भव हैं जिनमें वैकल्पिक स्वसिद्ध/आधारतत्व पाँचवें आधारतत्व का स्थान ले लेता है। यह वही निष्कर्ष था जिसे समझकर भी सच्चेरी घोषित करने का साहस नहीं कर पाए थे।
परन्तु गॉस को भी अपनी इस खोज को प्रकाशित करने का साहस नहीं हुआ। यहाँ मैं यह कहना चाहूँगा कि मुझे उनसे कोई हमदर्दी नहीं है। उनकी और सच्चेरी की परिस्थिति में बहुत अन्तर था। गॉस का रुतबा सच्चेरी की अपेक्षा कहीं अधिक था। गॉस धर्मगुरु नहीं थे और वैसे भी उस समय जर्मनी में चर्च का दबदबा सच्चेरी के समय की अपेक्षा काफी कम था। गॉस चाहे जितने भी प्रतिभाशाली हों, अन्तत: एक कायर थे।
लोबाचेव्स्की और बोल्यायी
अब हम पहुँचते हैं रूसी गणितज्ञ निकोलाइ इवानोविच लोबाचेव्स्की (1793-1856) तक। सन् 1826 में लोबाचेव्स्की भी इस बात पर विचार करने लगे कि कोई ज्यामिति यूक्लिडीय न होते हुए भी स्वसंगत हो सकती है। जैसे सच्चेरी ने सौ साल पहले किया था वैसे ही लोबाचेव्स्की ने भी न्यूनकोण ज्यामिति के प्रमेय सिद्ध करने शु डिग्री किए। परन्तु 1829 में लोबाचेव्स्की ने वह काम कर दिखाया जो न सच्चेरी कर सके थे, न गॉस। वह प्राप्त परिणामों से पीछे नहीं हटे और उन्हें प्रकाशित किया। किन्तु दुर्भाग्य यह रहा कि उन्होंने अपना लेख ‘ज्यामिति के सिद्धान्त’ रूसी भाषा में एक स्थानीय पत्रिका में प्रकाशित किया (वे प्रान्तीय रूस में काज़ान विश्वविद्यालय में काम करते थे।)।
अब भला रूसी भाषा कितने लोग पढ़ते हैं? लोबाचेव्स्की काफी हद तक अज्ञात रहे। फिर 1840 में उन्होंने अपना काम जर्मन भाषा में प्रकाशित किया। और तब वे विश्वभर के गणितज्ञों की नज़र में आए। लेकिन इसी दौरान हंगरी के गणितज्ञ जैनोस बोल्यायी (1802-60) भी इसी दिशा में काम कर रहे थे। बोल्यायी गणित के इतिहास में रोमांचक व्यक्तित्वों में से एक हैं। वे हंगरी के उच्चकुल की रीतियों के अनुसार वॉयलिन बजाने और तलवारबाज़ी में भी सिद्धहस्त थे। एक किस्सा है कि उन्होंने एक बार तेरह तलवारबाज़ों को एक के बाद एक परास्त किया और मुकाबलों के बीच में वायलिन बजाते रहे।
सन् 1831 में बोल्यायी के पिता ने गणित की एक पुस्तक प्रकाशित की। बोल्यायी कई साल से यूक्लिड के पाँचवें आधारतत्व के बारे में सोच-विचार कर रहे थे और उन्होंने अपने पिता को इसके लिए राज़ी कर लिया कि वे अपनी पुस्तक में एक 26 पन्ने का परिशिष्ट जोड़ दें जिसमें न्यूनकोण ज्यामिति का विवरण दिया गया था। यह सब लोबाचेव्स्की के रूसी लेख के प्रकाशन के दो साल बाद हुआ पर तब तक लोग लोबाचेव्स्की के बारे में नहीं जानते थे। आजकल साधारणतया लोबाचेव्स्की व बोल्यायी दोनों को गैर-यूक्लिडीय ज्यामिति (non-Euclidean geometry) का जनक माना जाता है।
अब क्योंकि बोल्यायी पिता-पुत्र ने अपनी पुस्तक जर्मन भाषा में प्रकाशित की, गॉस को तुरन्त इसके बारे में पता चल गया। यदि गॉस इस पुस्तक का अनुमोदन कर देते तो युवा बोल्यायी के लिए यह बहुत बड़ी बात होती। गॉस ने मौखिक रूप से ज़रूर बोल्यायी के काम की प्रशंसा की, पर अभी भी उनमें लिखित रूप से इसके बारे में कुछ कहने का साहस नहीं हुआ। लेकिन उन्हें सब्र नहीं हुआ और उन्होंने बोल्यायी को बताया कि सालों पहले यही विचार उनको भी आए थे परन्तु उन्होंने इन्हें प्रकाशित नहीं किया था। इस सम्बन्ध में अपना काम भी उन्हें दिखाया।
मेरे विचार में गॉस को ऐसा करने की कोई आवश्यकता नहीं थी। उसकी प्रसिद्धि स्थापित थी। गैर-यूक्लिडीय ज्यामिति को छोड़ दें, तो भी उनका कार्य दर्जन भर गणितज्ञों की उपलब्धियों के बराबर था। जब उन्हें खुद अपनी खोज प्रकाशित करने का साहस नहीं था तो फिर उन्हें बोल्यायी को इस खोज का श्रेय लेने देना चाहिए था। पर उन्होंने ऐसा नहीं किया। गॉस चाहे कितनी भी प्रखर बुद्धिवाले रहे हों कुछ मामलों में उनकी सोच काफी छोटी थी।
बेचारे बोल्यायी गॉस के इस खुलासे से इतने शर्मिन्दा और आहत हो गए कि उसके बाद उन्होंने गणित में आगे कुछ नहीं किया।
अधिक-कोण ज्यामिति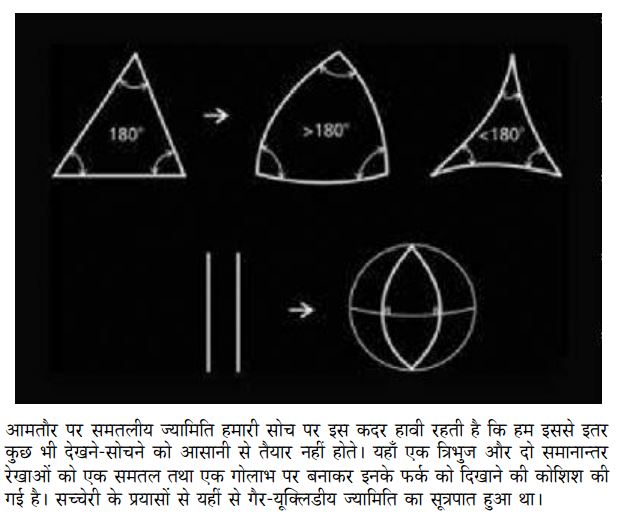
अब देखते हैं कि अधिक-कोण ज्यामिति का क्या हुआ। सच्चेरी ने अधिक-कोण ज्यामिति में एक विरोधाभास पाते ही उस पर आगे काम करना छोड़ दिया था। अब चूँकि एक गैर-यूक्लिडीय ज्यामिति (न्यूनकोण ज्यामिति) स्थापित हो ही गई तो फिर क्या अधिक-कोण ज्यामिति की रचना का भी कोई तरीका था? हाँ, था तो, पर यूक्लिडीय सिद्धान्तों से और भी हटने की कीमत पर। सच्चेरी ने अधिक-कोण ज्यामिति पर कार्य करते हुए एक अव्यक्त मान्यता/धारणा का उपयोग किया था जो यूक्लिड ने भी किया था। वह यह था कि कोई भी सरल रेखा असीमित हो सकती है अर्थात् अनन्त तक बढ़ाई जा सकती है। इस मान्यता से न्यूनकोण ज्यामिति या यूक्लिड की समकोण ज्यामिति में कोई विरोधाभास नहीं उत्पन्न हुआ पर अधिक-कोण ज्यामिति में इस मान्यता के कारण परेशानियाँ उठ खड़ी हुईं।
पर अगर, उसे भी छोड़ दें। अगर आप अपने सहज ज्ञान के विपरीत यह मान लेते हैं कि किसी भी सरल रेखा की लम्बाई सीमित ही होगी। ऐसा करने पर अधिक-कोण ज्यामिति के समस्त विरोधाभास गुम हो जाते हैं, एक दूसरी तर्कसंगत गैर-यूक्लिडीय ज्यामिति खड़ी हुई। ऐसी ज्यामिति का विवरण सबसे पहले 1854 में जर्मन गणितज्ञ जार्ज एफ. रीमान (1812-66) ने दिया।
इस तरह अब हमारे पास तीन तरह की ज्यामितियाँ हो गई हैं जिनमें अन्तर सिर्फ उस स्वसिद्ध का है जिसे पाँचवें आधार तत्व के स्थान पर रखा जाता है। ये हैं -
1) न्यूनकोण ज्यामिति (गैर-यूक्लिडीय): किसी सरल रेखा के बाहर के बिन्दु से होती हुई उस रेखा के समानान्तर असंख्य रेखाएँ खींची जा सकती हैं।
2) समकोण ज्यामिति (यूक्लिडीय): किसी सरल रेखा के बाहर के बिन्दु से होती हुई और उस रेखा के समानान्तर एक और सिर्फ एक रेखा खींची जा सकती है।
3) अधिक-कोण ज्यामिति (गैर-यूक्लिडीय): किसी सरल रेखा के बाहर के बिन्दु से होती हुई और उस रेखा के समानान्तर कोई भी रेखा नहीं खींची जा सकती है।
इन तीनों ज्यामितियों का यह अन्तर हम निम्न प्रकार से भी दिखा सकते हैं:
1) न्यूनकोण ज्यामिति: एक त्रिभुज के अन्त: कोणों का योग 1800 से कम होता है।
2) समकोण ज्यामिति: एक त्रिभुज के अन्त:कोणों का योग 1800 ही होता है।
3) अधिक-कोण ज्यामिति: एक त्रिभुज के अन्त:कोणों का योग 1800 से अधिक होता है।
अब प्रश्न यह उठता है कि इन तीनों में से कौन-सी ज्यामिति ‘सत्य’ है? अगर हम ‘सत्य’ का अर्थ अपने आप में स्वसंगत होना लें तो फिर तीनों ही ज्यामितियाँ सत्य मानी जाएँगी। ये एक-दूसरे के साथ ज़रूर स्वसंगत नहीं हैं और यह भी हो सकता है कि इनमें से शायद एक ही वास्तविक जगत के अनुरूप हो। तो हम यह प्रश्न कर सकते हैं कि इनमें से कौन-सी ज्यामिति हमारे वास्तविक संसार में मान्य होगी। इस प्रश्न का उत्तर फिर वही है कि तीनों ज्यामितियाँ मान्य हैं (यह कैसे हो सकता है, इसे आगे देखिए।)।
गोले की ज्यामिति
हम इस समस्या पर विचार करते हैं कि हमें अपनी पृथ्वी की सतह पर एक बिन्दु ॠ से दूसरे बिन्दु ए तक जाना है और वह भी ऐसे कि कम-से-कम दूरी तय करनी पड़े।
इस समस्या को थोड़ा सरल करने के लिए हम दो मान्यताएँ स्वीकार कर लेते हैं। पहली यह कि हम पृथ्वी को एक आदर्श, चिकनी, गोल सतह (ideal sphere) मान लेते हैं। यह बात काफी हद तक सही है; पृथ्वी के पर्वतों, घाटियों और भूमध्य रेखा के उभारों को पृथ्वी के व्यास की तुलना में नगण्य माना जा सकता है। दूसरी, हम यह मान लेते हैं कि हमें पृथ्वी की सतह पर ही चलना है अर्थात् हम सुरंग खोदकर अन्दर नहीं जा सकते।
अब पृथ्वी की सतह पर बिन्दु ॠ से बिन्दु ए तक सबसे कम दूरी वाला रास्ता पता करने के लिए हम यह कर सकते हैं कि ॠ से ए तक एक रस्सी तान लें। अगर यही चीज़ हम एक समतल पर करते तो हमें वह रास्ता मिलता जिसे हम सामान्यत: एक सरल रेखा कहते हैं।
परन्तु, एक गोले पर यह रेखा वक्र होगी। यह वक्र रेखा वास्तव में एक सरल रेखा के सदृश (analogous) होगी क्योंकि यह गोले की सतह पर दो बिन्दुओं के बीच न्यूनतम दूरी है। लेकिन हमेशा से हमारे अन्दर जो विचार बैठे हुए हैं उनके चलते इस बात को स्वीकार कर पाना मुश्किल है कि एक वक्र रेखा भी एक सरल रेखा के सदृश हो सकती है। इसलिए हम ‘सरल रेखा’ की जगह एक दूसरे शब्द का उपयोग करते हैं। किसी भी सतह पर दो बिन्दुओं के बीच की न्यूनतम दूरी को हम एक नया नाम देते हैं जियोडेसिक(Geodesic)।। 
एक समतल पर जियोडेसिक सरल रेखा होती है और एक गोले की सतह पर जियोडेसिक एक वक्र रेखा होती है जो कि एक ‘वृहद वृत्त’ (great circle) का वृत्त-खण्ड (arc) होता है। वृहद वृत्त उस वृत्त को कहते हैं जिसकी परिधि गोले की परिधि के बराबर होती है और जो ऐसे समतल में होता है जो गोले के केन्द्र से होकर जाता है। उदाहरण के लिए पृथ्वी पर भूमध्य रेखा एक वृहद वृत्त है और सारी देशान्तर रेखाएँ (Meridians) भी वृहद वृत हैं। किसी भी गोले पर असंख्य वृहद वृत्त खींचे जा सकते हैं। यदि गोले की सतह पर किन्हीं दो बिन्दुओं को एक तनी हुई डोरी से जोड़ा जाए तो वह रेखा सदा किसी-न-किसी वृहद वृत्त का वृत्त-खण्ड होगी।
अब यह आसानी से देखा जा सकता है कि गोले की सतह पर खींचा गया कोई भी वृहद वृत्त अपरिमित लम्बाई का नहीं हो सकता। अगर उसे बढ़ाया जाए तो किसी-न-किसी बिन्दु पर वह अपने आप से मिल जाएगा और एक संवृत्त वक्र (Closed Curve) बन जाता है। उदाहरण के लिए, पृथ्वी की सतह पर कोई भी जियोडेसिक 25,000 मील से लम्बी नहीं हो सकती। इसके अलावा किसी गोले पर खींची गई दो भिन्न जियोडेसिक रेखाएँ दो ही बिन्दुओं पर एक-दूसरे को काटती हैं। पृथ्वी पर कोई भी दो देशांश रेखाएँ एक-दूसरे को उत्तरी और दक्षिणी ध्रुव पर काटती हैं। इसका अर्थ यह हुआ कि यदि हम पृथ्वी की सतह पर कोई भी जियोडेसिक लें और कोई एक बिन्दु लें जो उस जियोडेसिक पर न हो तो उस बिन्दु से होकर कोई भी ऐसी जियोडेसिक नहीं खींची जा सकती जो पहली जियोडेसिक के समानान्तर हो। यह इसलिए कि उस बिन्दु से होकर जो भी जियोडेसिक खींची जाएगी वह पहली जियोडेसिक को दो बिन्दुओं पर काटेगी अर्थात् पृथ्वी पर कोई भी दो जियोडेसिक एक-दूसरे के समानान्तर नहीं हो सकतीं।
और यह भी देखिए। यदि गोले की सतह पर ऐसा त्रिभुज खींचा जाए जिसकी भुजाएँ वृहद वृत्तों के वृत्त-खण्ड हों, तो उस त्रिभुज के अन्त:कोणों का योग 1800 से अधिक होगा। इस कल्पना को मूर्त रूप देने के लिए आप एक ग्लोब की सहायता ले सकते हैं। इस पर ऐसे त्रिभुज की कल्पना कीजिए जिसका एक शीर्ष उत्तरी ध्रुव पर हो, एक भूमध्य रेखा पर 100 पश्चिमी देशान्तर पर हो और तीसरा भूमध्य रेखा पर ही 1000 पश्चिमी देशान्तर पर हो। यह एक समद्विबाहु त्रिभुज होगा जिसका हर अन्त:कोण 900 होगा अर्थात् इन अन्त:कोणों का कुल योग 2700 होगा।
रीमान द्वारा विकसित ज्यामिति बिलकुल ऐसी ही थी। इसमें जियोडेसिक रेखाओं को सरल रेखाओं के समतुल्य माना गया है। रीमान की ज्यामिति परिमित रेखाओं की ज्यामिति है जिसमें समानान्तर रेखाएँ नहीं होतीं और किसी भी त्रिभुज के अन्त:कोणों का योग 1800 से अधिक होता है। हम जिसे अभी तक ‘अधिक-कोण’ ज्यामिति कह रहे हैं, उसे ‘गोलीय’ ज्यामिति भी कहा जा सकता है और जिसे हम ‘समकोण’ या ‘यूक्लिडीय’ ज्यामिति कहते रहे हैं, उसे ‘समतल’ ज्यामिति भी कहा जा सकता है।
छद्म गोलाभ
सन् 1865 में एक और गणितज्ञ यूजिनियो बेल्टामी ने एक और आकार की ओर लोगों का ध्यान आकर्षित किया, जिसे Pseudosphere (छद्म गोलाभ) कहते हैं। यह आकृति आप चित्र में देख सकते हैं। यह देखने में ऐसी लगती है जैसे कि दो शहनाइयाँ चौड़े मुँह की तरफ से आपस में जोड़ दी गई हों और दूसरी तरफ अनन्त दूरी तक बढ़ा दी गई हों। आकृति के दोनों छोर सिकुड़ते जाएँ पर कभी पूरी तरह बन्द न हों। ऐसी आकृति पर खींची गई geodesic रेखाएँ न्यूनकोण ज्यामिति की आवश्यकताओं को पूरा करती हैं। किसी भी छद्म गोलाभ पर खींची गई जियोडेसिक की लम्बाई अपरिमित होती है। ऐसी दो जियोडेसिक खींचना सम्भव है जो अनन्त दूरी तक बढ़ाने पर भी एक-दूसरे को नहीं काटतीं अर्थात् एक-दूसरे के समानान्तर हों। यहाँ तक कि ऐसा भी सम्भव है कि दो जियोडेसिक एक-दूसरे को काटती हों और साथ ही एक तीसरी जियोडेसिक ऐसी हो कि वह पहली दोनों को ही किसी भी बिन्दु पर न काटे। अर्थात् पहली दो जियोडेसिक तीसरी के समानान्तर होंगी पर एक-दूसरे के नहीं।
यह बात बड़ी अटपटी लगती है क्योंकि हमें समतल ज्यामिति की ही आदत पड़ गई है, जहाँ जियोडेसिक सरल रेखाएँ होती हैं और एक-दूसरे को काटने वाली दो सरल रेखाएँ किसी भी तीसरी रेखा के समानान्तर नहीं हो सकतीं। पर छद्म गोलाभ पर जियोडेसिक इस तरह की वक्र रेखाएँ होती हैं कि ऐसा सम्भव है। वास्तव में, यदि हम दो जियोडेसिक लें जो एक-दूसरे को किसी बिन्दु पर काटतीे हों तो उनके बीच असंख्य ऐसी जियोडेसिक खींची जा सकती हैं जो उसी बिन्दु से होकर जाती हों और वे सब ऐसी जियोडेसिक के समानान्तर होंगी जो उस बिन्दु से होकर नहीं जाती। अर्थात् इस जियोडेसिक के समानान्तर और उसके बाहर के किसी बिन्दु से होते हुए असंख्य जियोडेसिक खींची जा सकती हैं। दूसरे शब्दों में, ‘न्यूनकोण ज्यामिति’ को हम ‘छद्म गोलाभ ज्यामिति’ भी कह सकते हैं।
पर फिर प्रश्न यह उठता है कि अपनी -अपनी जगह पर यदि ये तीनों प्रकार की ज्यामितियाँ स्वसंगत हैं तो फिर हमारे पूरे ब्रह्माण्ड के लिए इनमें से कौन-सी ज्यामिति सबसे सही है?
ब्रह्माण्ड की ज्यामिति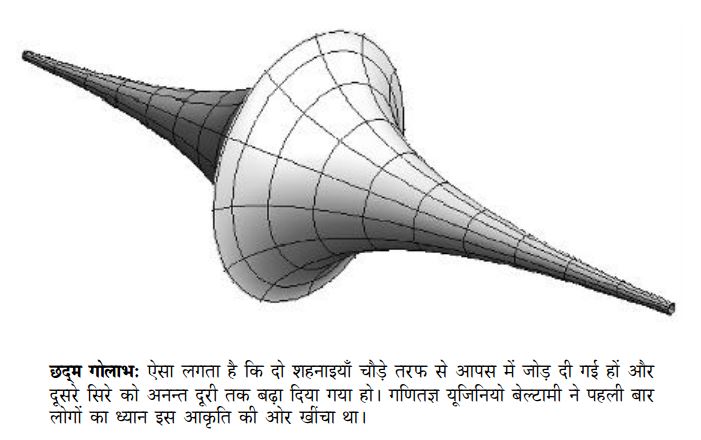
इस प्रश्न का उत्तर इतना आसान नहीं है। यदि हम दो गोले लें, एक छोटा और एक उससे काफी बड़ा और दोनों पर एक निश्चित लम्बाई की जियोडेसिक से त्रिभुज बनाएँ, तो दोनों त्रिभुजों के अन्त:कोणों का योग 1800 से अधिक होगा। किन्तु यह अन्तर छोटे गोले पर अधिक स्पष्ट होगा। हम गोले का आकार जितना बढ़ाते जाएँगेे अर्थात् त्रिभुज की भुजा की लम्बाई गोले के व्यास की अपेक्षा जितनी कम होती जाएगी, त्रिभुज के अन्त:कोणों का योग 1800 के उतना ही पास आता जाएगा। एक स्थिति ऐसी आएगी कि सूक्ष्म से सूक्ष्म नाप भी इस अन्तर को नहीं नाप पाएँगे। संक्षेप में, एक बड़े गोले की सतह का छोटा-सा हिस्सा समतल जैसा ही होता है और दोनों में अन्तर कर पाना सम्भव नहीं है।
यह बात पृथ्वी पर बिलकुल सही बैठती है। चूँकि पृथ्वी का आकार इतना बड़ा है, इसलिए उसके छोटे भाग बिलकुल समतल लगते हैं। यही कारण है कि मानव को यह स्वीकार करने में बहुत समय लगा कि पृथ्वी समतल न होकर गोल है। यही समस्या ब्रह्माण्ड के साथ भी है।
अन्तरिक्ष में प्रकाश एक बिन्दु से दूसरे बिन्दु तक बहुत लम्बी दूरियाँ भी तय करता है, जैसे सूर्य से पृथ्वी तक या एक आकाशगंगा से दूसरी आकाशगंगा तक। ये दूरियाँ पृथ्वी की सतह पर नापी जाने वाली किसी भी दूरी से बहुत, बहुत अधिक हैं। इन दूरियों के लिए खगोल शास्त्र में पारसेक (Parsec) इकाई उपयोग की जाती है। पारसेक वह दूरी है जो प्रकाश की किरण एक वर्ष में तय करती है अर्थात् लगभग चौरानबे खरब (94.6 ज्र् 1011) किमी.।
साधारणतया हम यह मान लेते हैं कि प्रकाश कई पारसेक की दूरियाँ भी सरल रेखा में तय करता है क्योंकि पृथ्वी पर किए गए मापन यही दिखाते हैं कि प्रकाश सरल रेखा में चलता है। परन्तु वास्तव में प्रकाश भी एक जियोडेसिक रेखा में चलता है और ज़रूरी नहीं है कि वह जियोडेसिक सरल रेखा हो। यदि ब्रह्माण्ड की ज्यामिति गैर-यूक्लिडीय (non-Euclidean) है तो ये जियोडेसिक वक्र रेखाएँ होंगी, सरल रेखाएँ नहीं।
गॉस के ध्यान में यह बात आई थी और उन्होंने एक परीक्षण किया। उन्होंने पृथ्वी पर तीन पर्वत चोटियों को त्रिभुज के शीर्ष मानकर, एक शीर्ष से दूसरे शीर्ष तक प्रकाश किरणें भेजीं और इस तरह बने त्रिभुज के अन्त:कोणों का योग नापा। यह योग तो 1800 ही आया, पर प्रश्न यह है कि क्या यह बिलकुल 1800 था? यदि ब्रह्माण्ड एक ऐसा गोला है जिसका व्यास कुछ अरब मील है और यदि प्रकाश किरणें इस गोले की वक्रता के अनुसार चलती हैं तो पृथ्वी जैसी छोटी सतह पर वर्तमान में उपलब्ध कोई भी माप त्रिभुज के अन्त:कोणों के योग का 1800 से अन्तर नहीं नाप पाएगा।
परन्तु सन् 1916 में आइंस्टाइन ने सामान्य सापेक्षता सिद्धान्त (General Theory of Relativity) की खोज की। इस सिद्धान्त की रचना करते समय जब वे गुरुत्वाकर्षण को समझाने लगे तो उन्होंने पाया कि गुरुत्वाकर्षण की सही व्याख्या तभी हो सकती है जब यह मान लिया जाए कि ब्रह्माण्ड में प्रकाश (और बाकी सब भी) गैर-यूक्लिडीय जियोडेसिक रेखाओं में चलता है, सरल रेखा में नहीं।
आइंस्टाइन के सिद्धान्त के अनुसार ब्रह्माण्ड गैर-यूक्लिडीय है और उसमें ‘अधिक-कोण’ ज्यामिति लागू होती है।
संक्षेप में, यूक्लिड की ज्यामिति जिसे दो हज़ार वर्ष तक परम शाश्वत सत्य माना जाता था, वास्तव में बहुत सीमित सिद्धान्त है, जो सिर्फ समतल पर लागू होता है। पृथ्वी की सतह या ब्रह्माण्ड के लिए यह लगभग सही है, पूरी तरह नहीं। यूक्लिड की ज्यामिति समग्र सत्य नहीं, सिर्फ सम (तल) सत्य है।
मूल लेख: आइज़ेक एसीमोव।
अँग्रेज़ी से अनुवाद: रमा चारी: राजा रमन्ना सेंटर फॉर एडवांस्ड टेक्नॉलॉजी, इन्दौर से सम्बद्ध हैं। विज्ञान शिक्षण व अनुवाद में रुचि।
यह लेख एसीमोव के संकलन ‘द एज ऑफ टुमॉरो’ (The Edge Of Tomorrow) से साभार।
आइज़ेक एसीमोव: बीसवीं शताब्दी में विज्ञान को लोगों तक पहुँचाने में जिन वैज्ञानिकों का महत्वपूर्ण योगदान रहा है - उनमें से एक हैं आइज़ेक एसीमोव। विज्ञान गल्प को भी वे नईऊँचाइयों तक लेकर गए। उन्होंने बहुत-सी पुस्तकें भी लिखीं हैं, उनकी किताबों की कुल संख्या सैकड़ों में होगी।