लेखक: श्रेया खेमानी
अनुवाद: विवेक मेहता [Hindi PDF, 217 kB]
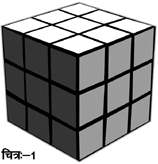
आम तौर पर हम सममिति यानी सिमैट्री (Symmetry) को आकार का एक गुण मानते हैं। लेकिन यह गणित में भी शामिल है। किसी भी सममित चीज़ को कुछ ऐसे बदला जा सकता है कि वह बदली अवस्था में भी सम का गुण न खोए। ये तरीके क्या हैं, कितने हैं और इनके ज़रिए सममित चीज़ों का विश्लेषण कैसे किया जा सकता है हम गणित की ग्रुप थियरी के ज़रिए समझ सकते हैं। भौतिकशास्त्र और रसायनशास्त्र में ही नहीं, सममिति का सामना हम अपनी आम ज़िन्दगी में भी करते हैं जैसे रूबिक क्यूब, गद्दी, उपरोक्त जैसे कई पैटर्न इत्यादि। इन सबके बारे में हमारी समझ बढ़ती है ऐसी गणितीय सोच से।1974 में एरनो रूबिक ने एक ऐसे खिलौने का आविष्कार किया जिसने आज तक लोगों को अपने सम्मोहन में बाँधकर रखा है। आपने भी शायद कभी-न-कभी इस रंगीन और जादुई खिलौने को देखा होगा जिसे हम आज रूबिक क्यूब के नाम से जानते हैं। आप में से कइयों ने शायद इस खिलौने की पहेली को हल करने की कशमकश में घण्टों बिताए होंगे। और कुछ लोगों को इसे हल करने में सफलता भी मिली होगी। पर यह भी हो सकता है कि आपको इसके बारे में कुछ भी न पता हो। ऐसे लोगों के लिए नीचे एक अनछुए रूबिक क्यूब का चित्र दिया गया है (चित्र-1)। क्यूब का हर एक तल नौ वर्गों से मिलकर बना हुआ है और चित्र में क्यूब की जो अवस्था दिखाई गई है उसमें हर एक तल पर जो वर्ग हैं, वे एक ही रंग के हैं। असल में ये वर्ग उन छोटे-छोटे क्यूब के ही तल हैं जिनसे मिलकर रूबिक क्यूब बना हुआ है। अगर क्यूब को हाथों में पकड़कर तलों को कुछ समय के लिए घुमाया जाए तो आप पाएँगे कि तलों के रंग मिल-जुल गए हैं और क्यूब को उसकी शुरुआती अनछुई स्थिति में पहुँचाने का कोई स्पष्ट तरीका नहीं है। क्यूब को उसकी अनछुई स्थिति में पहुँचाने की यह पहेली ही इस खेल की चुनौती है।
 अक्सर ही इस खिलौने के बारे में लोग यह कहते हुए मिल जाते हैं कि यह कितना मैथेमैटिकल या गणितीय खेल है।
अक्सर ही इस खिलौने के बारे में लोग यह कहते हुए मिल जाते हैं कि यह कितना मैथेमैटिकल या गणितीय खेल है।
कई बार लोग किसी खिलौने, संगीत की धुन या किसी डिज़ाइन के बारे में कहते हैं कि वह निहायत गणितीय है - “कितना गणितीय है यह”। इस बात को वे ऐसे लहज़े में कहते हैं कि मन करता है ‘गणितीय’ की जगह ‘सुन्दर’ शब्द रखा जा सकता है। या शायद ‘सुन्दर और रहस्यमय’ कहना बेहतर होगा। आपको क्या लगता है, ऐसा कहने वालों का क्या आशय होता है?
आखिर एक रूबिक क्यूब में ऐसा क्या है जो उसे गणितीय बनाता है? इस मासूम-से लगने वाले खिलौने में ऐसा क्या मिला जिसके चलते गणितज्ञों ने इससे जुड़े गणितीय गुणों का विश्लेषण करते हुए कई शोधपत्र लिख डाले? यकीनन, इसके पीछे का कारण इतना साधारण तो हो नहीं सकता कि रूबिक क्यूब एक रेगुलर पोलिहेड्रन (नियमित बहुतल) है। एरनो रूबिक स्वयं भी एक गणितज्ञ नहीं थे। द्वितीय विश्व युद्ध के दौरान हवाई-हमलों से बचने के लिए आश्रयालय बने बूडापेस्ट के एक अस्पताल में एक कवि और विमान-इंजीनियर के घर जन्मे रूबिक ने आर्किटेक्चर का अध्ययन किया और बाद में इंटीरियर डिज़ाइन पढ़ाने लगे। उन्हें शायद इस बात का अन्दाज़ा नहीं था कि उनका बनाया खिलौना कुछ ही सालों में इतना विख्यात हो जाएगा। 1982 का साल आते-आते रूबिक क्यूब घर-घर में पहुँचने लगा था और ऑॅक्सफोर्ड इंग्लिश डिक्शनरी का हिस्सा बन चुका था। दुनियाभर में अब तक दस करोड़ से भी ज़्यादा रूबिक क्यूब बेचे जा चुके हैं।1
रूबिक क्यूब, गणित व सममिति
रूबिक क्यूब पर एक सतही निगाह डालने पर हम पाते हैं कि - इस खिलौने में न तो कोई नम्बर है, और न ही कोई समीकरण हल करना है - तो फिर इसमें गणितीय हुआ क्या? लेकिन अगर हम यह सवाल पूछें कि “रूबिक क्यूब को कितने सम्भावित तरीकों से जमाया जा सकता है?” या यह कि “तलों की मिले-जुले रंगों वाली व्यवस्था से इसे कितने चरणों में शुरुआती स्थिति में लाया जा सकता है?” तो इनके जवाब ढूँढ़ने के लिए हमें गणित का रुख करना होगा। गणित की वह शाखा जो इन सवालों के जवाब देती है हमें एक ऐसे संसार में लेकर जाती है जो बहुत ही आश्चर्यजनक है - और वो संसार है सममिति का। दरअसल, आम तौर पर, यह सममिति ही है जो किसी ‘गणितीय’ कला या संगीत के नमूने या रूबिक क्यूब जैसे खिलौने में पाई जाती है। तो यह बात समझने से पहले कि सममिति का गणित से क्या लेना-देना है, आइए हम इस बात की समझ बनाने की कोशिश करते हैं कि आखिर सममिति से हमारा मतलब क्या है और इसे कैसे ‘मापा’ जा सकता है।
सममिति के गुण-नियम
हम किसी चीज़ को समरूप तब कहते हैं जब एक से अधिक दृष्टियों से देखने पर वो एक ही जैसी दिखाई दे। उदाहरण के तौर पर, ऐसा माना जाता है कि इन्सानी शरीर में द्विपक्षीय सममित होती है क्योंकि हमारा दायाँ भाग व बायाँ भाग लगभग एक जैसे होते हैं व जब हम एक आइने के सामने खड़े होते हैं तो हम और हमारा प्रतिबिम्ब लगभग एक समान ही होते हैं। वहीं छत पर लटके हुए पंखे में तीनपक्षीय घूर्णी-सममिति होती है - अगर हम पंखे को 120 डिग्री (जो 360 डिग्री के कोण का तीसरा हिस्सा है) घुमाएँ तो पहले वाली और नई स्थिति में कोई भी अन्तर नहीं नज़र आता।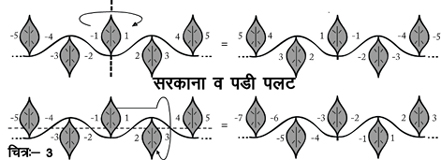 अब दीवार पर उतारे गए चित्र-3 को देखिए। एक पड़ी/लेटी रेखा पर आगे सरकाने व उसी रेखा को सन्दर्भ मान घुमाते हुए और एक खड़ी रेखा को सन्दर्भ मान कर पलटने से चित्र में उकेरे गए पैटर्न पर कोई असर नहीं पड़ता। ऐसे पैटर्न जो एक आयाम में अपने आप को दोहराते हों, फ्रीज़ पैटर्न (frieze pattern)) कहलाते हैं।
अब दीवार पर उतारे गए चित्र-3 को देखिए। एक पड़ी/लेटी रेखा पर आगे सरकाने व उसी रेखा को सन्दर्भ मान घुमाते हुए और एक खड़ी रेखा को सन्दर्भ मान कर पलटने से चित्र में उकेरे गए पैटर्न पर कोई असर नहीं पड़ता। ऐसे पैटर्न जो एक आयाम में अपने आप को दोहराते हों, फ्रीज़ पैटर्न (frieze pattern)) कहलाते हैं।
तो हम कैसे इन वस्तुओं व छवियों की सममिति माप सकते हैं? क्योंकि हम चीज़ों या पैटर्न के आकार या संरचना पर विचार कर रहे हैं ना कि रंग जैसे गुणों पर, इसलिए ‘एक जैसे दिखने’ कहने की बजाय अन्य कुछ ऐसी स्थितियों के बारे में सोचते हैं जिसमें वो छवि या पैटर्न उसी आयाम के स्थान में फिट हो जाए। सममिति मापने के लिए हम उन तमाम तरीकों की एक लिस्ट बनाते हैं जिनसे हम उस वस्तु को दोबारा से ऐसे व्यवस्थित कर सकें कि वो अपनी शुरुआती अवस्था के स्थान पर व आकार जैसी ही बनी रहे।
जब हम रूबिक क्यूब की बात करते हैं, तो हम उसके छोटे-छोटे क्यूब के अलग-अलग संयोजनों को देख रहे होते हैं। क्यूब को कुछ इस तरह से डिज़ाइन किया गया है कि इसे किसी भी तरह से घुमाने पर यह दोबारा उसी आकार में आ जाता है जिसमें यह पहले था। ऐसे में क्यूब के संयोजनों का अध्ययन करने का मतलब होगा उसकी सममिति का अध्ययन करना।
आप शायद अब भी सोच रहे होंगे कि इन सब में आखिर गणित कहाँ है। असल में, क्यूब के भागों के अलग-अलग संयोजन मिलकर एक समूह बनाते हैं जिसे गणितज्ञ ‘ग्रुप’ (group) कहते हैं। ऐसे समूह निश्चित नियमों का पालन करते हैं और समान तरीके से व्यवहार भी करते हैं। इन समूहों में निहित आधारभूत संरचना का अध्ययन व किसी सार्थक तरीके से उनका वर्गीकरण हमें इनके व्यवहार की भविष्यवाणी करने में सक्षम बनाता है।
आइए अब ज़रा रूबिक क्यूब को गौर से अवलोकन करते हुए एक ग्रुप की अनौपचारिक या स्थूल समझ बनाने की कोशिश करते हैं।
रूबिक क्यूब का डिज़ाइन उन सम्भावित तरीकों की संख्या पर एक सीमा निर्धारित करता है जिनसे उसे घुमाया जा सकता है। वास्तव में, हम कह सकते हैं कि ऐसे केवल 6 तरीके ही हैं - 6 तलों में से हर एक को 90 डिग्री से घड़ी की घूमने की दिशा में घुमाना। बेशक, आप चाहें तो किसी तल को 180 डिग्री घड़ी की दिशा में या 90 डिग्री घड़ी की उल्टी दिशा में भी घुमा सकते हैं। लेकिन यह किसी तल को दो या तीन दफे घड़ी की दिशा में 90 डिग्री से घुमाने के बराबर ही होगा। और 360 डिग्री से घुमाने का मतलब कुछ ना करने के बराबर ही हुआ। तो, इससे हम अपने पहले महत्वपूर्ण अवलोकन या निष्कर्ष तक पहुँचते हैं कि -
* पूर्वनिर्धारित तरीकों (चाल/मूव्स/निर्देशों) की एक ऐसी सूची है जो कभी नहीं बदलती।
इस तरह से आप क्यूब के किसी भी तल को कितना भी घुमाएँ, आप उसे उतना ही उल्टा घुमा कर पहले की स्थिति में आ सकते हैं। जिसका मतलब हुआ कि -
* हर क्रिया उलटनीय यानी रिवर्सिबल है।
किसी ताश के खेल की तरह जहाँ आपकी हार या जीत हाथ में आए पत्तों पर निर्भर करती है या पासा फेंकने से जुड़ा कोई खेल जिसमें आपको पता ही नहीं होता कि अगली बार पासा फेंकने पर कौन-सा नम्बर आएगा, रूबिक क्यूब चांस या संयोगों पर निर्भर कोई खेल नहीं है। इसमें आप जब भी किसी तल को घुमाते हैं तो उसका एक पूर्वानुमानित परिणाम होता है जो किसी भी तरह से घुमाने वाले के कौशल या भाग्य पर निर्भर नहीं करता। जिसके चलते -
* हर कार्रवाई के परिणाम का पहले से ही पता लगाया जा सकता है।
और अन्त में, तलों को किसी अनुक्रम में घुमाने से बनी कुल कार्रवाई भी अपने आप में एक कार्रवाई है, बशर्ते यह कुल कार्रवाई पूर्वनिर्धारित सूची में हमारे द्वारा सूचीबद्ध बुनियादी कदमों के संयोजन से बनी हो। इस पर कोई पाबन्दी नहीं है कि इन कदमों को किस क्रम में लागू किया जाए। बुनियादी कदमों का एक अनुक्रम क्यूब को ऐसी स्थिति में पहुँचा देता है जहाँ से किसी अन्य अनुक्रम को भी लागू किया जा सकता है। तो हम कह सकते हैं कि -
* किसी भी क्रम में लागू किए गए बुनियादी कदमों की कुल कार्रवाई भी एक क्रिया है।
क्यूब के बारे में हम अन्य कई अवलोकन कर सकते हैं। लेकिन फिलहाल के लिए हमारी दिलचस्पी उन गणितीय परिणामों में ही है जो कि इन चार अवलोकनों के कारण होंगे। ये अवलोकन ही क्यूब की सममिति का वर्णन करने के लिए पर्याप्त हैं। अगर हम इन अवलोकनों की व्याख्या नियमों के तौर पर करें तो अनौपचारिक तरीके से हम कह सकते हैं कि एक ग्रुप ऐसे कदमों या कार्रवाइयों का एक संग्रह है जो कि इन चार नियमों का पालन करते हों।2
रूबिक क्यूब का हल
अब सवाल उठता है कि कैसे इन नियमों की मदद से हम क्यूब के बारे में कुछ जान-समझ सकते हैं। या यह कि कैसे इनकी मदद से हम क्यूब की पहेली को हल कर सकते हैं। अव्यवस्थित क्यूब को मात्र देखकर ही इस बात का अन्दाज़ा लगा पाना लगभग हमेशा ही असम्भव होता है कि किस तरीके से घुमाने से यह दोबारा से व्यवस्थित हो जाएगा। ऐसे में क्यूब की भूलभुलैया में फँसे किसी इन्सान की शायद सबसे बड़ी मदद होगी कि कहीं से उसे उन बुनियादी कदमों का एक अनुक्रम मिल जाए जो उसे क्यूब की पहेली हल करने की दिशा में आगे बढ़ा सके। यह ठीक उस नक्शे जैसा होगा जो आपकी वर्तमान स्थिति से आपको उस तरफ जाने का रास्ता सुझाए जिधर आप जाना चाहते हों। इस तरह का एक नक्शा बनाने का मतलब हुआ कि क्यूब की तमाम सम्भावित स्थितियों (विन्यासों) और उन स्थितियों के बीच के सम्बन्धों को दर्शाना।
एक-दूसरे तरीके से हम यह कह सकते हैं हमें बुनियादी कदमों के सभी अनुक्रमों को देखना होगा और साथ ही यह भी कि उनके बीच के आपसी सम्बन्ध कैसे हैं। हमने पहले ही देखा कि रूबिक क्यूब से जुड़ी चालें या कार्रवाईयाँ मिलकर एक ग्रुप बनाती हैं। 6 बुनियादी कदमों से मिलकर बनी कार्रवाइयों की एक विस्तृत सूची के सदस्य ही इस ग्रुप के सदस्य होंगे। और जिस नक्शे की बात हम कर रहे हैं वो इन तमाम सम्भावित कार्रवाइयों से बने इसी ग्रुप का एक नक्शा होगा। रूबिक क्यूब पर कई किताबें व शोधपत्र हैं जो हमें यह जानकारी देते हैं। लेकिन, जैसा कि आप कल्पना भी कर सकते हैं कि ऐसा नक्शा असाधारण रूप से बड़ा होगा। और यह है भी। इस ग्रुप का आकार (यानी कि कार्रवाइयों की कुल संख्या) है 43252003274489856000 - एक इतनी बड़ी संख्या जिसे पढ़ना भी अपने आप में एक बड़ा काम है। साफ ज़ाहिर है कि रूबिक क्यूब के लिए इतना बड़ा नक्शा बनाना कोई बच्चों का खेल नहीं और न ही इस लेख में हम यह कोशिश करेंगे। लेकिन हम एक सरल-सा उदाहरण लेकर उसके नक्शे से जुड़ी अवधारणाओं की समझ बनाने की कोशिश तो कर ही सकते हैं।
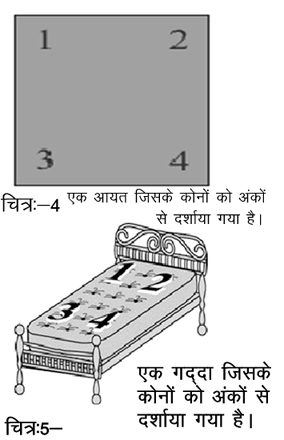 चित्र-4 में दिए आयत को देखिए। अगर हममें इस आयत की सममितिओं की बात करें तो हम उन सभी सम्भावित स्थितियों या विन्यासों व उनके संयोजनों के बारे में सोचना होगा जिससे इस आयत को इसके शुरुआती स्थान में ही रख सकें। आसानी के लिए आप आयत को बिस्तर पर रखे एक गद्दे के रूप में सोच सकते हैं (चित्र-5) जिससे जुड़ा यह सवाल आपको पूछना है कि ‘कितने तरीकों से गद्दे को बिस्तर फ्रेम में फिट बैठाया जा सकता है?’
चित्र-4 में दिए आयत को देखिए। अगर हममें इस आयत की सममितिओं की बात करें तो हम उन सभी सम्भावित स्थितियों या विन्यासों व उनके संयोजनों के बारे में सोचना होगा जिससे इस आयत को इसके शुरुआती स्थान में ही रख सकें। आसानी के लिए आप आयत को बिस्तर पर रखे एक गद्दे के रूप में सोच सकते हैं (चित्र-5) जिससे जुड़ा यह सवाल आपको पूछना है कि ‘कितने तरीकों से गद्दे को बिस्तर फ्रेम में फिट बैठाया जा सकता है?’
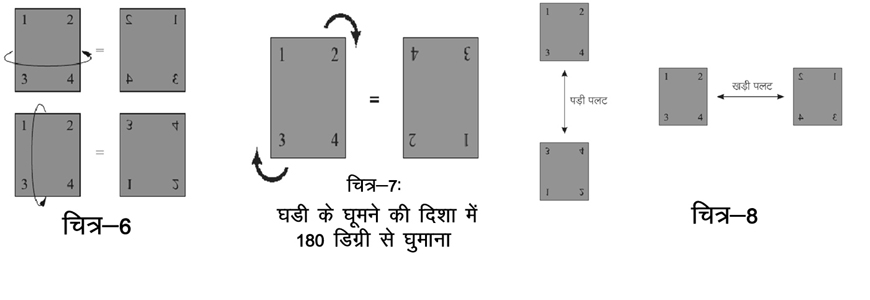
दो सम्भावित उत्तर जो झट से हमारे दिमाग में आते हैं वो गद्दे को उसकी लम्बाई व चौड़ाई को सन्दर्भ मान कर पलटने से मिलते हैं। आसानी के लिए हम इन्हें खड़ी पलट ‘H’ (लम्बाई को सन्दर्भ मान कर दी गई पलट) व पड़ी पलट ‘V’ (चौड़ाई को सन्दर्भ मान कर दी गई पलट) कह लेते हैं (चित्र-6)।
कोई चाहे तो गद्दे को 180 डिग्री से घड़ी के घूमने की दिशा में भी घुमा सकता है (चित्र-7) (चाहें तो इसे 180 डिग्री से घड़ी के घूमने की विपरीत दिशा में भी घुमाया जा सकता है, लेकिन यह 180 डिग्री से घड़ी की दिशा में घुमाने के समान ही होगा)।
अब हमें इन चालों के संयोजनों को देखना होगा। गौर कीजिए कि लम्बाई को सन्दर्भ मान गद्दे को दो बार पलटने से हम पहली वाली स्थिति में ही पहुँच जाते हैं। इसी तरह चौड़ाई को सन्दर्भ मान गद्दे को दो बार पलटने से हम पहली वाली स्थिति में ही पहुँच जाते हैं। इस तरह हम कह सकते हैं किHH=VV=N(जहाँ ग़् वो चाल हुई जिसमें कुछ भी नहीं किया गया)। तीरों की मदद से हमे इसे कुछ ऐसे दिखा सकते हैं जैसे चित्र-8।
अगर हम एक खड़ी पलट के बाद एक पड़ी पलट का इस्तेमाल करें तो नतीजा वैसे होगा जैसे चित्र-9 में दर्शाया गया है।
इसी तरह एक पड़ी पलट के बाद एक खड़ी पलट का नतीजा भी यही होगा। इसके अलावा, गद्दे को 180 डिग्री घुमाने का नतीजा भी यही होगा (चित्र-7 को देखिए)। तो हम कह सकते हैं कि HV=VH=R क्योंकि R, H और V के संयोजन से ही बना है, इसलिए इस पर अलग से ध्यान देना ज़रूरी नहीं। जिसका मतलब हुआ कि हमारा लेना-देना सिर्फ दो चालों से ही है - खड़ी पलट (H) और पड़ी पलट (V)।
आगे बढ़ने से पहले आप यह सुनिश्चित कर लें कि ये दोनों चालें उन चार नियमों का पालन करती हैं जिन्हें हम पहले परिभाषित कर चुके हैं। ऐसा कर लेने के बाद इस ग्रुप से जुड़ा नक्शा बनाने के लिए ज़रूरत होगी कि चालों के सभी संयोजनों को देखें-परखें। ऐसा करने की प्रक्रिया में हम इस ग्रुप के तमाम सदस्यों को सूचीबद्ध कर लेंगे व साथ ही उनके आपसी सम्बन्धोंें की समझ भी बना सकेंगे। एक चित्र की मदद से हम इसे बढ़िया तरीके से दर्शा सकते हैं (चित्र-10)।
आयत की सममितियों का ग्रुप
बेशक, रूबिक क्यूब के मामले की ही तरह यहाँ भी चालों का संयोजन किसी भी क्रम में किया जा सकता है। आप शायद सोच रहे हों कि इस तरह तो चालों के अनगिनत संयोजन बनाए जा सकते हैं। और क्या वे सभी इस सममिति के ग्रुप के सदस्य नहीं होंगे? आप कुछ संयोजन बनाकर देखिए। आप पाएँगे कि चालों के किसी भी संयोजन का आयत पर परिणाम इन चारों में से एक ही होगा: कोई बदलाव नहीं (N), खड़ी पलट (H), पड़ी पलट (V), खड़ी पलट व पड़ी पलट (HV)। उदाहरण के लिए, चालों के इस संयोजन को देखिए: खड़ी पलट - पड़ी पलट - पड़ी पलट - खड़ी पलट। चित्र-10 में दिखाए गए नक्शे से यह साफ ज़ाहिर है कि इस संयोजन का आयत पर कोई असर नहीं होगा। प्रतीकों में कहें तो HVVH=N अनौपचारिक तरीके से ही सही लेकिन कोशिश कीजिए तर्क देने की कि ऐसा क्यों सही है।
चित्र-10 असल में आयत की समरूपताओं के समूह का पूरा नक्शा है! रूबिक क्यूब की ही तरह - अगर हमारे सामने यह पहेली हो कि आयत की किसी भी स्थिति से हमें उसे उसकी शुरुआती स्थिति में ले जाना हो तो यह नक्शा हमें वो रास्ता सुझा देगा जिसकी मदद से हम इस पहेली को हल कर सकते हैं।
प्राथमिक स्कूल की गुणन-सारणी की ही तरह प्रतीकों का इस्तेमाल कर हम इस नक्शे के लिए एक सारणी तैयार कर यह दर्शा सकते हैं कि इस ग्रुप के सदस्य कैसे-कैसे संयोजन बनाते हैं व उन संयोजनों का आयत पर क्या असर होता है (चित्र-11)।
 आम ज़िन्दगी में आयत की सममिति के ग्रुप के उदाहरण
आम ज़िन्दगी में आयत की सममिति के ग्रुप के उदाहरण
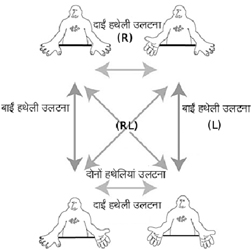
आयत की सममिति को दर्शाता यह ग्रुप, बिजली के स्विच की एक जोड़ी से जुड़े तर्क से लेकर पानी के अणुओं की सममिति जैसी कुछ अप्रत्याशित जगहों पर भी दिख जाता है। जैसा कि स्टीवन स्ट्रोगेटज़ लिखते हैं ‘यह ग्रुप थियरी से जुड़े आकर्षणों में से एक है। यह थियरी एकदम अलग-सी लगने वाली चीज़ों में भी अन्तर्निहित समानता को उजागर कर देती है। जैसा कि भौतिक विज्ञानी रिचर्ड फाइऩमेन से जुड़ा वो मज़ेदार किस्सा जिसके चलते उन्हें युद्ध के समय सेना की टुकड़ी में भेजे जाने से मोहलत मिल गई। जाँच करने के लिए जब सेना के मनोचिकित्सक ने उनसे अपने दोनों हाथ दिखाने के लिए कहा तो फाइनमेन ने एक हथेली ऊपर और दूसरी नीचे रखते हुए हाथ आगे बढ़ा दिए। जब चिकित्सक ने कहा, “नहीं ऐसे नहीं, दूसरी तरह से” तो फेनमैन ने दोनों हथेलियों को पलट दिया - सीधी हथेली को उल्टा और उल्टी हथेली को सीधा। फाइनमेन असल में सिर्फ एक दिमागी खेल ही नहीं खेल रहे थे बल्कि वो ग्रुप थियरी से जुड़े एक छोटे-से मज़ाक में व्यस्त थे।’ उन सभी तरीकों के बारे में सोचिए जिनका इस्तेमाल फाइनमेन चिकित्सक को अपनी दोनों हथेलियाँ दिखाने के लिए कर सकते थे। इन सभी तरीकों को चित्र-12 में दिखाया गया है।
क्या यह कुछ जाना-पहचाना-सा लग रहा है? प्रतीक चिन्ह R का इस्तेमाल दाईं हथेली को पलटने, L को बाईं हथेली को पलटने, RL को दोनों हथेलियों को पलटने व N को कुछ भी न करने, के लिए करते हुए एक सारणी बनाइए। अब इसकी तुलना आयत के लिए बनाई गई सारणी से कीजिए। आप देखेंगे कि यह आयत की सममितिओं के ग्रुप के पैटर्न का ही पालन करता है। क्या यह अपने आप में कमाल नहीं कि कैसे हमने दो एकदम अलग-अलग व असम्बन्धित स्थितियों में एक समान पैटर्न खोज निकाला?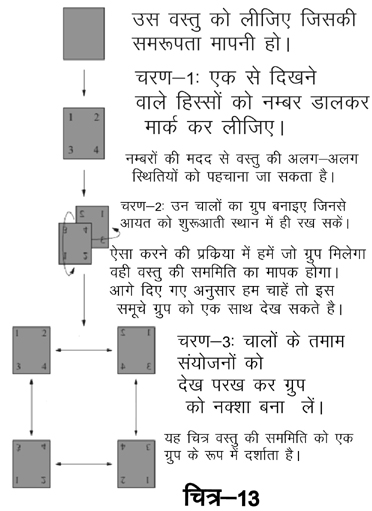 आश्चर्यजनक तौर पर एकदम अलग-अलग सन्दर्भों के बीच के कनेक्शन देखने में ग्रुप थियरी हमारी मदद करती है। ग्रुप की अवधारणा का इस्तेमाल न जाने कितनी ही जगहों पर सममितिओं का वर्णन करने के लिए किया जाता है - संख्याओं के संसार और अणुओं व क्रिस्टल के आकार से लेकर स्मारकों की दीवारों पर पाए जाने वाले फ्रीज़ पैटर्न तक। ग्रुप थियरी की सुन्दरता इस बात में है कि यह हमें एक ऐसा तरीका सुझाती है जिसकी मदद से हम अप्रत्याशित स्थानों में भी एक-जैसे पैटर्न पहचान सकते हैं। किसी खास वस्तु या पैटर्न में अन्तर्निहित ग्रुप की संरचना को पहचानने की प्रक्रिया में हम चीज़ों में छुपी हुई उस समानता का अनुभव करते हैं जिसका ज़िक्र स्ट्रोगेटज़ ने किया है। साथ ही हम ताज्जुब में पड़ जाते हैं कि कैसे गणित जैसा विषय हमारे आस-पास की दुनिया व घटनाओं की असरदार तरीके से व्याख्या करता है। उदाहरण के लिए, हमें ऐसा लग सकता है कि फ्रीज़ पैटर्न बनाने की अनगिनत सम्भावनाएँ हो सकती हैं - लेकिन ग्रुप थियरी हमें बतलाती है कि किसी भी फ्रीज़ पैटर्न को मात्र 7 में से एक ही ग्रुप की मदद से समझा जा सकता है। इसी तरह सभी वॉलपेपर पैटर्न (दीवारों पर बनाए या चिपकाए जाने वाले पैटर्न) - जो दो आयामों में फैले पैटर्न हैं - सिर्फ 17 में से किसी एक ग्रुप का ही हिस्सा हो सकते हैं! ऐसा माना जाता है कि स्पेन के भव्य महल अलहम्ब्रा की दीवारों पर इन सभी 17 वॉलपेपर ग्रुप से सम्बन्धित पैटर्न हैं।
आश्चर्यजनक तौर पर एकदम अलग-अलग सन्दर्भों के बीच के कनेक्शन देखने में ग्रुप थियरी हमारी मदद करती है। ग्रुप की अवधारणा का इस्तेमाल न जाने कितनी ही जगहों पर सममितिओं का वर्णन करने के लिए किया जाता है - संख्याओं के संसार और अणुओं व क्रिस्टल के आकार से लेकर स्मारकों की दीवारों पर पाए जाने वाले फ्रीज़ पैटर्न तक। ग्रुप थियरी की सुन्दरता इस बात में है कि यह हमें एक ऐसा तरीका सुझाती है जिसकी मदद से हम अप्रत्याशित स्थानों में भी एक-जैसे पैटर्न पहचान सकते हैं। किसी खास वस्तु या पैटर्न में अन्तर्निहित ग्रुप की संरचना को पहचानने की प्रक्रिया में हम चीज़ों में छुपी हुई उस समानता का अनुभव करते हैं जिसका ज़िक्र स्ट्रोगेटज़ ने किया है। साथ ही हम ताज्जुब में पड़ जाते हैं कि कैसे गणित जैसा विषय हमारे आस-पास की दुनिया व घटनाओं की असरदार तरीके से व्याख्या करता है। उदाहरण के लिए, हमें ऐसा लग सकता है कि फ्रीज़ पैटर्न बनाने की अनगिनत सम्भावनाएँ हो सकती हैं - लेकिन ग्रुप थियरी हमें बतलाती है कि किसी भी फ्रीज़ पैटर्न को मात्र 7 में से एक ही ग्रुप की मदद से समझा जा सकता है। इसी तरह सभी वॉलपेपर पैटर्न (दीवारों पर बनाए या चिपकाए जाने वाले पैटर्न) - जो दो आयामों में फैले पैटर्न हैं - सिर्फ 17 में से किसी एक ग्रुप का ही हिस्सा हो सकते हैं! ऐसा माना जाता है कि स्पेन के भव्य महल अलहम्ब्रा की दीवारों पर इन सभी 17 वॉलपेपर ग्रुप से सम्बन्धित पैटर्न हैं।
हाल ही में प्राथमिक स्कूल के पाठ्यक्रम में समरूपता की अवधारणा को जगह दी गई है। मेरा ऐसा मानना है कि अनिश्चित रूप से ही सही, पर हम सभी यह समझते हैं कि इसका गणित से कुछ लेना-देना तो है, लेकिन वास्तव में यह क्या बला है यह बात इतनी स्पष्ट नहीं थी। एक आयत की सममितियों के ग्रुप को देखने से आपको गणित और सममिति के बीच के रिश्ते को समझने में मदद मिली होगी। इस उदाहरण की मदद से आपका परिचय उस ग्रुप को खोजने की तकनीक से भी कराया गया है जो किसी वस्तु की सममिति की व्याख्या करता हो। संक्षेप में आयत का उदाहरण चित्र-13 में दोहराया गया है। चित्र वस्तु की सममिति को एक ग्रुप के रूप में दर्शाता है।
स्नातक स्तर पर दूसरे या तीसरे साल तक ग्रुप थियरी की पढ़ाई नहीं होती। ऐसे में प्राथमिक स्कूल के पाठ्यक्रम में समरूपता का समावेश जायज़ है या नहीं, यह तो मैं नहीं कह सकती लेकिन कम-से-कम अगर अगली बार ज़ाहिराना तौर पर समरूप दिखने वाली किसी वस्तु को देखकर कोई यह कहता मिल जाए कि, “यह बहुत गणितीय है” तो आप मुस्कुराते हुए कह सकती हैं कि, “मैं शायद समझती हूँ कि आप क्या कहना चाहते हैं।”
श्रेया खेमानी: गणित में स्नातकोत्तर और एकलव्य के गणित पाठ्यक्रम शोध व सामग्री विकास समूह से सम्बद्ध हैं। रायपुर, छत्तीसगढ़ में एक मज़दूर संगठन के स्कूल के साथ भी काम करती हैं। गणित शिक्षा-शिक्षण में उनकी रुचि गणित और राजनीति के इंटरसेक्शन को जाँच-समझने की इच्छा से उभरती है। उनसे
अँग्रेज़ी से अनुवाद: विवेक मेहता: आई.आई.टी., कानपुर से मेकेनिकल इंजीनियरिंग में पीएच.डी. की है। इन दिनों स्वतंत्र रूप से लिखने व अनुवाद का काम करते हैं।
चित्र: स्टीवन स्ट्रोगेटज़ के लेख ‘ग्रुप थिंक’ और नाथन कार्टर की किताब ‘विज़ुअल ग्रुप थियरी’ से और इंटरनेट कीविभिन्न वेबसाइट से लिए गए हैं।



