शून्य पर समझ

मनोज कुमार शराफ

अगर मैं आपसे पूछूँ कि ओ, डक और लव में क्या समानता है, तो आप या तो थोड़ा चुप रहेंगे या कहेंगे कि कुछ भी समानता नहीं या कहेंगे कुछ समानता हो सकती है, पर अभी मुझे सूझ नहीं रहा है। चलिए, आपकी कुछ मदद कर देते हैं। आपने बेड्मिनटन के खेल के दौरान रेफरी को ‘लव ऑल' कहते ज़रूर सुना होगा। अब आप कुछ-कुछ अन्दाज़ लगा रहे होंगे कि यहाँ ‘लव ऑल' का क्या मतलब हो सकता है। थोड़ा आगे बढ़ते हैं और सोचते हैं कि क्रिकेट में कहे जाने वाले शब्द ‘डक' के आखिर क्या मायने हैं। अभी भी न समझ में आया हो तो ‘ओ' को अँग्रेज़ी में कैसे लिखते हैं, इस पर विचार करें।

हाँ, आप सही समझे, मैं शून्य की  ही बात कर रहा था। शून्य जिसे अरबी-उर्दू में सिफर, अँग्रेज़ी में ज़ीरो तथा अमेरिकन लोग ‘ओ' या ‘नॉट' पढ़ते, लिखते और समझते हैं।
आप इस लेख को जिस कम्प्यूटर या मोबाइल पर पढ़ रहे हैं, वह भी द्वि-आधारित संख्या पद्धति यानी - ‘ज़ीरो' और ‘एक' के आधार पर चलता है। शून्य के बिना कोई भी आधुनिक इलेक्ट्रॉनिक उपकरण मौजूद ही नहीं होंगे। शून्य के बिना इन उपकरणों से कोई गणना सम्भव नहीं है जिसका अर्थ है कि शून्य के उपयोग के बिना आधुनिक इंजीनियरिंग या स्वचालित मशीनों की कल्पना भी सम्भव नहीं है। वास्तव में, हमारी आधुनिक दुनिया का ज़्यादातर हिस्सा शून्य के बिना अधूरा रह जाएगा।

शून्य एक गेम चेंजर
इस तरह देखें तो मानव द्वारा शून्य की खोज (आविष्कार) एक ‘गेम चेंजर' साबित हुआ है। लेकिन क्या आपको पता है कि मानव इतिहास  में हज़ारों साल तक शून्य का कहीं अता-पता ही नहीं था। शून्य की अवधारणा आ भी गई तब भी काफी समय तक मानव ने इसे  संख्या नहीं समझा। उपरोक्त बातों से एक बात तो तय है कि शून्य प्रकृति-प्रदत्त नहीं है। हमने शून्य का अपनी सुविधा या कहें आवश्यकता-पूर्ति हेतु   आविष्कार किया है। और हमें इसे अगली पीढ़ी को भी सिखाना होगा। मैंने सुना है कि वैज्ञानिकों ने विभिन्न शोध में यह पाया है कि कई जानवर, जैसे बन्दर, मधुमक्खी ‘कुछ भी नहीं' की अवधारणा को न केवल समझते हैं बल्कि छोटी मधुमक्खी तो अपने  दिमाग में शून्य की गणना भी कर सकती है। लेकिन केवल मनुष्यों ने  न केवल शून्य की अवधारणा को समझ लिया है बल्कि उसकी सहायता से कई स्वचालित उपकरणों का आविष्कार भी कर लिया है।

शून्य की समझ
तो आइए, जानने की कोशिश करते हैं कि यह अति उपयोगी किन्तु विचित्र शून्य आखिर है क्या।
जब आप इस बात पर विचार करते हैं तो पाते हैं कि प्रकृति में हम शून्य का सामना शायद कभी नहीं करते हैं। अगर हम शून्य को एक, दो और तीन जैसी संख्याओं की तरह   मूर्त चीज़ों से सम्बद्ध कर पाते जैसे एक आम, दो किताब, चार दिशाएँ आदि तो शायद शून्य की हमारी समझ और गहरी होती। हम ‘एक' प्रकाश पुंज को देख सकते हैं। हम कार के हॉर्न से ‘दो' बीप सुन सकते हैं। लेकिन क्या शून्य को देख या सुन सकते हैं? शायद नहीं! ऐसे में हमें यह समझने के लिए काफी मशक्कत करनी होगी कि किसी चीज़ की अनुपस्थिति भी अपने आप में एक चीज़ है।
हार्वर्ड विश्वविद्यालय के एक  गणित के प्रोफेसर और शून्य पर  पुस्तक लिखने वाले रॉबर्ट कपलान कहते हैं, “शून्य दिमाग में है, लेकिन संवेदी दुनिया में नहीं है।” यहाँ तक कि सूने अन्तरिक्ष में भी शून्य नहीं है क्योंकि आप वहाँ तारों को देख सकते हैं। तो इसका मतलब है कि शायद एक सच्चा शून्य - जिसका अर्थ पूर्ण शून्यता है - बिग बैंग से पहले के समय में अस्तित्व में रहा हो लेकिन हम इस बात को कभी प्रमाणित नहीं कर सकते कि कभी पूर्ण शून्यता की स्थिति भी रही होगी। वास्तव में, शून्य मौजूद नहीं है, फिर भी हम शून्य की अवधारणा का उपयोग अन्य सभी संख्याओं को प्राप्त करने के लिए कर सकते हैं।

रॉबर्ट कपलान का प्रयोग  
सबसे पहले रॉबर्ट कपलान ने  एक प्रयोग के माध्यम से शून्य को  समझाने का प्रयास किया जिसे गणितज्ञ जॉन वॉन न्यूमैन द्वारा कुछ इस तरह वर्णित किया गया है। वॉन न्यूमैन, रॉबर्ट कपलान के इस प्रयोग का वर्णन सरल किन्तु भ्रामक प्रयोग के रूप में करते हैं।
-    यह प्रयोग कुछ इस तरह है कि एक बॉक्स की कल्पना करें जिसमें कुछ भी नहीं है। यह शून्य का भौतिक प्रतिनिधित्व है। चित्र-1 में आप देख सकते हैं कि खाली बॉक्स के अन्दर क्या है। कुछ भी तो नहीं।
- अब एक और खाली बॉक्स लें, और इसे पहले वाले बॉक्स के अन्दर  रख दें। अब पहले बॉक्स में कितनी चीज़ें हैं? देखें (चित्र-2) इसमें एक वस्तु है।
- अब इस अन्दर वाले बॉक्स के अन्दर एक और खाली बॉक्स डाल दें। अब इसमें कितनी वस्तुएँ हैं? आप कहेंगे - दो।
- आप देख रहे होंगे कि कैसे हम शून्य से सभी गिनती (संख्या) प्राप्त करते जा रहे हैं, यह सोचने वाली बात है न?
क्या शून्य वास्तव में कुछ भी नहीं है? नहीं! यह हमारी संख्या प्रणाली की जान है।
शून्य एक ही समय में एक अमूर्त विचार और एक वास्तविकता है। कपलान अपने इस प्रयोग के आधार पर शून्य के बारे में कहते हैं, “शून्य हमारे मन-मस्तिष्क में संख्या के संसार को उसी तरह भर देता है जिस तरह एक खाली केनवास में एक पूरी तस्वीर को उकेरा जा सकता है। यदि आप शून्य को देखते हैं तो आप कुछ भी नहीं देखते हैं। लेकिन अगर आप इसे समझते हैं, तो आप संख्याओं की दुनिया को देखते हैं। यह एक क्षितिज की तरह है जहाँ लाखों-अरबों सितारे टिमटिमाते हैं।
एक बार हमने शून्य होने को आत्मसात कर लिया, तो हमारे लिए  ऋणात्मक संख्याओं की समझ भी आसान हो जाएगी। शून्य हमें यह समझने में मदद करता है कि हम गणित का उपयोग उन चीज़ों के बारे में सोचने के लिए भी कर सकते हैं जिनकी मूर्त रूप से या कहें भौतिक वस्तुओं से कोई सम्बद्धता सम्भव नहीं है।

गणित में शून्य क्यों उपयोगी है?
आइए, जानते हैं कि आज के  हमारे गणित के लिए शून्य किस तरह से उपयोगी है।
आधुनिक गणित में शून्य का उपयोग दो तरह से हो रहा है।
एक - यह हमारी संख्या प्रणाली में एक महत्वपूर्ण स्थान धारक अंक है: मानव इतिहास में शून्य का पहला  उपयोग आज से कोई 5,000 साल पहले प्राचीन मेसोपोटामिया में मिलता  है। वहाँ, इसका उपयोग अंकों की एक रस्सी (कुछ-कुछ आज की गिन माला की तरह) में अंकों की अनुपस्थिति को दर्शाने अर्थात उसका  प्रतिनिधित्व (represent) करने के लिए किया गया था।
 इसे एक उदाहरण से समझते हैं, एक संख्या ‘103' के बारे में सोचिए। इस संख्या में शून्य ‘दहाई  कॉलम'  में ‘कुछ भी नहीं है' के लिए है। अतः यह एक स्थान धारक है, जो हमें यह समझने में मदद करता है कि उपरोक्त संख्या ‘एक सौ तीन' है, न कि ‘13'।

क्या आपको याद है कि रोमनों ने अपनी संख्या कैसे लिखी थी? रोमन अंकों में 103 को CIII लिखते हैं। संख्या 99 को XCIX लिखते हैं। अब  आप CIII + XCIX को जोड़ने का प्रयास करें। यह तार्किक ढंग से या आसान विधि से कर पाना सम्भव नहीं है, बेतुका है। शून्य अपने आप में एक उपयोगी संख्या है। लेकिन प्राचीन रोमन लोगों को यह पता नहीं था जिसके कारण उन्हेेें अपनी संख्याओं के साथ संक्रिया करने में काफी कठिनाई होती थी जैसा कि आपने CIII एवं XCIX के मामले में देखा। शून्य की मदद से स्थानीय मान के आधार पर बनाई गई संख्या प्रणाली के ज़रिए हम आसानी-से संख्याओं को जोड़ने-घटाने का काम कर पाते हैं। यह प्रणाली ज़रूरत पड़ने पर हमें उनमें  हेरफेर करने की अनुमति भी देती है यानी उधार लेने, हासिल आने (regrouping) की इजाज़त देती है। स्थानीय मान के आधार पर स्थापित किए गए संख्या संकेत हमें किसी कागज़ की शीट पर जटिल-से-जटिल  गणितीय समस्याओं को हल करने की व्यवस्था देते हैं।
दो - शून्य एक संख्या के रूप में:  यदि शून्य केवल एक स्थान धारक  अंक ही बना रहता, तो भी यह अपने आप में अति उपयोगी सिद्ध होता। लेकिन लगभग 1,500 साल पहले (या शायद पहले भी), भारत में शून्य एक  नम्बर (संख्या) बन गया, जो ‘कुछ भी नहीं' को दर्शाता है। उसके बाद    मध्य अमेरिका एवं अन्य प्राचीन सभ्यताओं ने भी अपनी संख्या प्रणाली में शून्य को स्वतंत्र रूप से एक संख्या के रूप में मान्यता दे दी।

याद रहे, सातवीं शताब्दी में, भारतीय गणितज्ञ ब्रह्मगुप्त ने लिखा कि “जब किसी संख्या में शून्य जोड़ा जाता है या किसी संख्या से घटाया जाता है, तो संख्या अपरिवर्तित रहती है; और शून्य से गुणा होने वाली संख्या शून्य हो जाती है।” इस कथन को शून्य के अंकगणित के पहले  लिखित विवरण के रूप में मान्यता प्राप्त है।
यूरोप पहुँचने से पहले धीरे-धीरे शून्य मध्य-पूर्व में फैल गया, और 1200 के दशक में गणितज्ञ फिबोनाची ने ‘अरबी' अंक प्रणाली को लोकप्रिय बनाया, जिसका हम सभी आज भी उपयोग करते हैं। वहाँ से, शून्य की उपयोगिता का विस्तार हुआ। उस सदी में गणित का एक नया क्षेत्र भी देखा गया जो शून्य के साथ अन्य संख्याओं की गणना पर निर्भर करता है।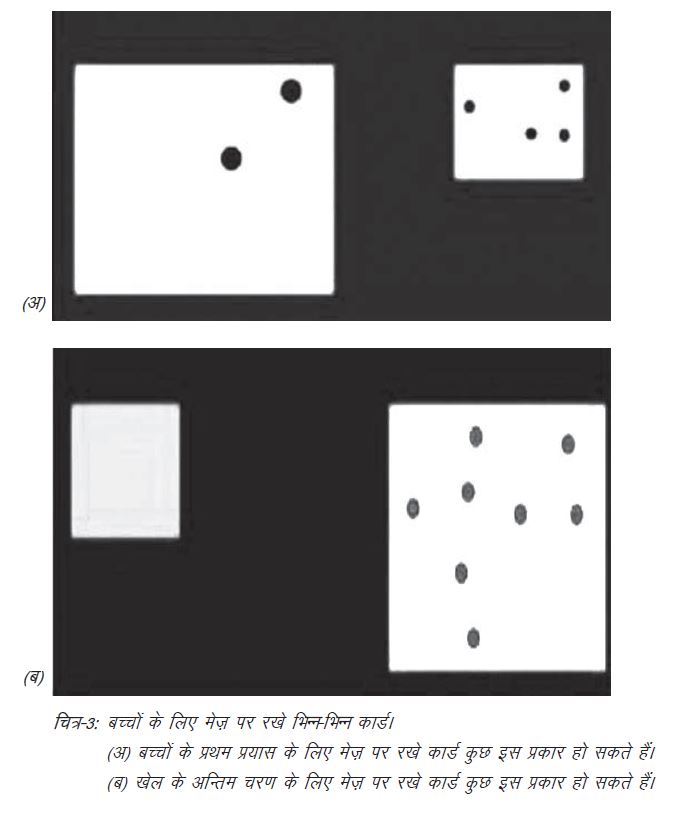

शून्य भी एक संख्या
ड्यूक विश्वविद्यालय में मनुष्य और जानवर के दिमाग में संख्याओं की धारणा का अध्ययन करने वाली  एक न्यूरोसाइंटिस्ट एलिज़ाबेथ ब्रोंकॉन बताती हैं कि “जब आप 6 वर्ष से छोटे बच्चे को ‘शून्य' का अर्थ ‘कुछ भी नहीं है' समझाते हैं और जब आप एक बच्चे से पूछते हैं कि कौन-सी संख्या छोटी है, शून्य या एक, तो वे अक्सर सबसे छोटी संख्या के रूप में ‘एक' को व्यक्त करते हैं; तब समझ लीजिए कि उनके लिए गणित को समझने का कठिन समय है।”
गणितज्ञ ब्रानोन कहते हैं, “यह सीखना सबसे मुश्किल है कि शून्य एक से छोटा है।”
आइए, इसके लिए ब्रोनोन द्वारा बताए गए एक खेल का हिस्सा बनते हैं। इस खेल का नाम है ‘सबसे कम को चुनिए'।

ब्रानोन अक्सर 4 साल के बच्चों के साथ एक खेल खेलते हैं जिसमें वे एक जोड़ी कार्ड को एक मेज़ पर रख देते हैं और प्रत्येक कार्ड पर अलग-अलग चित्र बने होते हैं। मसलन, एक कार्ड पर दो बिन्दु होंगे। तो दूसरे कार्ड पर तीन बिन्दु बने होंगे। चित्र-3 में उनके कार्ड का चित्र आपके समझने के लिए दिया जा रहा है। फिर बच्चों को सबसे कम संख्या वाले कार्ड उठाने को कहा जाता है। जब तक दोनों कार्ड में कुछ बिन्दु बने होते हैं तब तक बच्चों को चयन करने में कोई परेशानी नहीं होती परन्तु जैसे ही मेज़ पर ‘कुछ नहीं' वाला कार्ड और एक बिन्दु वाला कार्ड रखा जाता है, तो आधे से भी कम बच्चों के द्वारा सही उत्तर दिया जाता है। मेरी सलाह है कि किसी कक्षा में बच्चों के साथ या फिर शिक्षकों के साथ  आप भी इस खेल को खेलकर देखें। आपको भी आश्चर्य होगा बशर्ते आप शून्य को एक संख्या मानते हों।

शून्य के चार मनोवैज्ञानिक चरण  
जर्मनी के संज्ञानात्मक वैज्ञानिक एंड्रियास निडर ने कहा कि शून्य को समझने के लिए चार मनोवैज्ञानिक चरण होते हैं, और प्रत्येक चरण संज्ञानात्मक रूप से पहले की तुलना में अधिक जटिल होता  है।  धरती के कई जानवर पहले तीन चरणों को किसी-न-किसी तरीके से पार कर जाते हैं। लेकिन अन्तिम चरण उनके लिए सबसे कठिन होता है। या कहें अन्तिम चरण को केवल हम मनुष्य ही पार कर पाते हैं।
पहला चरण संवेदी अनुभव नोटिस करना है। जैसे कोई टिमटिमाती  रोशनी जो जल और बुझ रही  है। या किसी मोटर के हॉर्न से निकली बीप जैसी आवाज़ जो चालू और बन्द हो रही है, इसे नोटिस करने की क्षमता मनुष्य सहित सभी जानवरों में पाई जाती है क्योंकि यह काफी सरल संवेदी अनुभव है जिसे सभी जानवर महसूस कर सकते हैं।
दूसरा चरण व्यवहारगत समझ यानी प्रतिक्रिया देना है। इस स्तर पर, न केवल जानवर एक उत्तेजना (stimuli) की कमी को पहचान सकते हैं, वे इस पर प्रतिक्रिया भी कर सकते हैं। जैसे जब उन्हें अपनी भोज्य वस्तु की अनुपस्थिति का पता चलता है तो वे किसी अन्य भोज्य पदार्थ की ओर जाना और अन्य भोज्य वस्तु के बारे में जानना चाहते हैं।

तीसरा चरण यह मानना है कि  शून्य (या एक खाली कंटेनर), एक से कम मूल्य रखता है। मधुमक्खियों और बन्दरों सहित कई जानवरों के लिए यह मानना  थोड़ा  मुश्किल है, पर वे इस तथ्य को भी जानते हैं कि शून्य का मूल्य एक से कम है या कहें किसी वस्तु के नहीं होने की बजाय उस वस्तु का होना ज़्यादा मूल्यवान है।
चौथा चरण शून्य को एक प्रतीक के रूप में मानना है। यहाँ एक उत्तेजना की अनुपस्थिति को एक प्रतीक के रूप में मान्यता दी जाती है  और समस्याओं को हल करने के लिए एक तार्किक उपकरण के रूप में इस्तेमाल किया जाता है। मनुष्यों के अलावा अन्य कोई जानवर नहीं है जो  जानता हो कि शून्य का एक प्रतीक हो भी सकता है।
लेकिन अच्छी तरह से शिक्षित मनुष्य भी शून्य के बारे में सोचते हुए थोड़ी चूक कर सकता है। अध्ययनों से पता चला है कि वयस्कों को भी अन्य अंकों की तुलना में शून्य को  संख्या के रूप में मानने में कुछ  ज़्यादा समय लगता है। जब बर्नोन का ‘सबसे कम को चुनिए' वाला  प्रयोग वयस्कों के साथ दोहराया गया तो वे शून्य और एक के बीच का निर्णय लेते समय, शून्य से एक बड़ी संख्या की तुलना करने के समय से थोड़ा अधिक समय लेते हैं। यानी 1 और 0 की तुलना में लगने वाला समय, 2 और 3 की तुलना में लगने वाले समय से ज़्यादा होता था।  
उपरोक्त बातों से पता चलता है कि शून्य को एक संख्या के रूप में स्थापित करने और उसका मान एक से कम साबित करने के लिए काफी  मशक्कत करनी पड़ती है। रॉबर्ट कपलान कहते हैं, “संख्याओं से जुड़ी गणित की सभी संक्रियाएँ शून्य की अवधारणा के चारों ओर नृत्य करती हैं।” हालाँकि, हम शून्य की समझ के साथ पैदा नहीं हुए हैं परन्तु मेरे विचार में एक गणित शिक्षक होने के नाते हम सभी को शून्य की अवधारणा की गहरी समझ होनी चाहिए। हमें शून्य की अवधारणा को समझना ही होगा, भले ही इसमें थोड़ा अधिक वक्त लगे।

मनोज कुमार शराफ: विभिन्न विद्यालय जैसे ट्रिनिटी कॉन्वेंट, विद्या भारती, लायन्स स्कूल तथा डी.ए.व्ही. में गणित शिक्षक के रूप में करीब 27 वर्षों तक अध्यापन कार्य। पिछले तीन वर्षों से अज़ीम प्रेमजी फाउंडेशन, रायपुर में बतौर गणित विशेषज्ञ के रूप में कार्यरत।