रूस के किसानों का गुणा एक दुगुना तो एक आधा
संदर्भ के 17वें अंक में जरा सिर तो खुजलाइए स्तंभ में एक सवाल पूछा गया था - रूस के किसानों के गुणा करने के तरीके से जुड़ा। इसका एक जवाब अंक 18 में छपा था जिसमें 'द्विअंकीय पद्धति (Binary System)' से इसके हल के बारे में समझाया गया था। लेकिन इसे सवाल के बारे में सोचने के और भी तरीके मौजूद हैं। इस बार इन तरीकों के साथ ही 18वें अंक में पूछी गई ‘पहिए वाली उलझन' की चर्चा और साथ में एक नई गुत्थी ‘सिर खुजलाने' के लिए।
संदर्भ के 17वें अंक में एक सवाल था - रूस के किसानों के गुणा करने के तरीके के बारे में। कोई दो आंकड़े हैं - 23 और 16.
एक आंकड़े को दुगना करते जाओ और दूसरे को आधा करते जाओ जब तक एक न आ जाए।
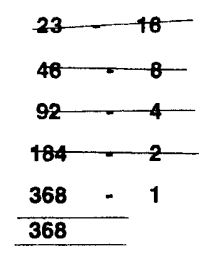
सम संख्या के सामने के आंकड़े काट दो, बचे आंकड़ों को जोड़ लो तो गुणा का सही जवाब आ जाता है। ऐसा क्यों हुआ?
इसलिए कि दो संख्याएं 9 और 6 का गुणनफल अगर 54 है तो एक अंक को आधा और दूसरे को दुगना करने पर गुणनफल उतना ही रहेगा -
9 x 6 = 54
9 x 2 x 6/2 = 54 होगा
इसलिए
23 x 16 = 368
46 X 8 = 368
92 x 4 = 368
184 x 2 = 368
368 x 1 = 368
अगर भाग देने वाले आंकड़े में विषम संख्या न आए तो जहां एक आएगा उसके सामने वाले गुणनफल का आंकड़ा उतने गुना होगा जितना भाग देने वाला आंकड़ा है - जैसे 368, 23 का 16 गुना है।
एक दूसरा
23 -- 13
46 -- 6
92 -- 3
184 -- 1
भाग देने वाले आंकड़े में अगर विषम संख्या आ जाए तो हम ऊपर का बचा हुआ एक छोड़ देते हैं। सम संख्या के सामने के आंकड़े काट दीजिए बचे आंकड़ों का जोड़ 23 X 13 का गुणनफल होगा।
यहां 23 x 2 तो हो गया पर 132 करने पर 1 बाकी रहा और इस एक को हम छोड़ देते हैं। यानी कि यहां पर हम 23 का एक गुना अर्थात 23 छोड़ रहे हैं। (276 + 23 = 299)
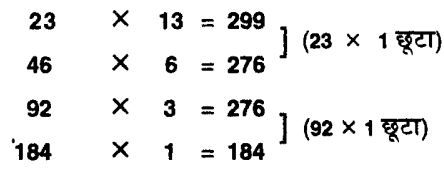
और इसी तरह अंत में 3 का आधा करने पर एक छूटा। यहां पर हम 92 को एक गुना छोड़ रहे हैं।
अतः विषम संख्या को 2 से विभाजित करने में जहां-जहां एक छूट रहा है। उसके असर को जोड़ना पड़ेगा हीः
23 x 13 = 299 (13 में से 1 छूटा)
46 x 6 = 276 + 23 = 299
92 x 3 = 276 + 23 = 299 (3 में से 1 छूटा)
184 x 1 = 184+23 + 92=299
यह एक और तरीका है इस सवाल को समझने का। इस हल तक पहुंचने में मुझे गणित की प्रारम्भिक प्रक्रियाएं ही करनी पड़ी, द्विअंकी पद्धति या किसी अन्य विशेष सिद्धांत की ज़रूरत नहीं लगी। परन्तु इस हल तक पहुंचने के लिए जोड़ तोड़ करते वक्त मुझे संख्याओं के बारे में कई नई बातें पता चली, शायद वे सब गणित की दृष्टि से अत्यन्त सामान्य होंगी परन्तु खुद खोजकर किसी बात को समझो तो आनंद आता ही है।
(यह जवाब भेजा था मुकेश मालवीय, सहायक शिक्षक, प्राथमिक शाला पावरझंडा, तहसील शाहपुर, ज़िला बैतूल, म.प्र. ने)
इसी सवाल के दो और सही हल आए हैं।
प्रमोद मैथिल ( सरदार पटैलपुरा वार्ड नंबर 3, पुरानी इटारसी ) ने सही जवाब देने के बाद सुझाया है कि दो की बजाए तीन से गुणा और भाग करते हुए भी ऐसी ही विधि विकसित की जा सकती है। एक उदाहरण लेकर उन्होंने यह भी दर्शाया है कि यह विधि थोड़ी जटिल है। क्या आप सोचना चाहेंगे कि ऐसा कैसे हो सकता है और क्या जटिलता है इस तरीके में।
मोहम्मद रज्ज़ाक ( बालागंज, होशंगाबाद ) का कहना है कि इस तरीके में एक तरफ दशमलव संख्या भी ली जा सकती है शर्त केवल इतनी है कि उस संख्या को ही दुगना करने के लिए चुना जाए। उनके शब्दों में, दो से भाग देने की तरफ दशमलव संख्या रखने पर इस विधि की सीमा आ जाती है। ऐसा क्यों?



