रामकृष्ण भट्टाचार्य
चितियां बनाने के लिए कितनी ज्यामिति की आवश्यकता थी?
सोमयज्ञ के लिए कई सारे सा पण्डाल लगाने पड़ते हैं, जिनके लिए बहुत बड़ी जगह की ज़रूरत पड़ती है। इसके लिए कई सारी अग्नियों, चितियों, वेदियों और मण्डपों की जटिल व्यवस्था भी ज़रूरी होती है। अगले पेज पर याज्ञिक क्षेत्र का एक रेखाचित्र प्रस्तुत किया गया है। इसमें अनावश्यक संरचनाएं नहीं दर्शाई गई हैं। (देखिए चित्र-1)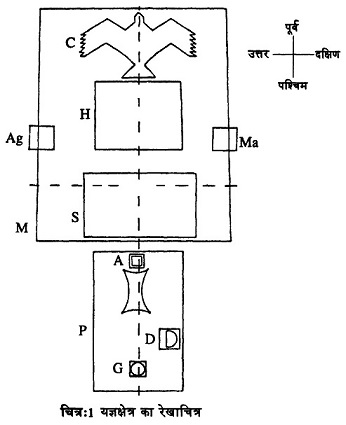 
यज्ञ क्षेत्र की जमावट
पश्चिम दिशा में स्थित अपेक्षाकृत छोटा घेरा (P) प्राग्वंश मण्डप कहलाता है। इसमें एक वृत्ताकार अग्नि (गार्हपत्य अग्नि, G) जिस पर बलि दिए गए जंतु को सर्वप्रथम पकाया जाता है। इसमें एक अर्द्ध वृत्ताकार अग्नि (दक्षिण अग्नि, D) भी होती है। एक वर्गाकार बलि वेदी, आहवनिया-अग्नि A होती है जिस पर अग्नि की स्थापना की जाती है। बड़े घेरे, M को महावेदी कहते हैं। इसकी आकृति एक समद्विबाहु समलंब के समान होती है और इसमें एक रेखा पूर्व से पश्चिम की ओर तथा दूसरी रेखा उत्तर से दक्षिण की ओर जाती है। इन्हें क्रमश: प्राची व उदिची कहते हैं। प्राची को पृष्ट्या (पृष्ठ यानी पीठ) भी कहा जाता है। एक मायने में यह महावेदी की रीढ़ है। यह सममिति की रेखा है। महावेदी का निर्माण यज्ञ शुरू हो जाने के बाद किया जाता है। यह एक नवीन बलि वेदी होती है जो पुरानी का स्थान ले लेती है। चित्र में नई वेदी को धुर पूर्व में दर्शाया गया है। इसका आकार एक बाज़ (श्येन) के समान है जिसके डैने मुड़े हुए हैं और पूंछ फैली हुई (वक्रपक्ष व्यस्तपुच्छ) है। अलबत्ता यह वेदी अन्य आकृतियों में भी बनाई जा सकती है। इसकी आकृति दरअसल यजमान की मनोकामना पर निर्भर है। मसलन, यदि वह ब्रह्मलोक प्राप्त करना चाहता है, तो चिति कूर्म (कछुए) के आकार की बनाई जाएगी। यदि उसे शत्रुओं को पछाड़ाना है तो चिति का आकार रथचक्र के समान होगा क्योंकि वेदों में कहा गया है, "रथ किसी वज्र के समान है जिसे यजमान अपने शत्रुओं पर फेंकता है। बहरहाल, श्येन तो प्रकृति है और यह ऐसी समस्त चितियों का प्रतिनिधित्व करती है।
महावेदी के अंदर आयताकार घेरा 5 सदस कहलाता है। यह मंत्रोच्चार कक्ष है। मध्य में निर्मित वर्गाकार घेरा Hहविर्धान कहलाता है। इसका शाब्दिक अर्थ है 'बलि संग्राहक'। यह वह स्थान है जहां सोम वनस्पति लाने वाले वाहनों को रखा जाता है और अनुष्ठान के दौरान इन पौधों को पीसा जाता है। महावेदी के उत्तर व दक्षिण की ओर एक-एक वर्गाकार घेरा है (Ag तथा Ma) जिन्हें क्रमशः अग्निघ्रिया तथा मार्जालिया मण्डप कहते हैं।
अग्नियों के विविध उल्लेख
यज्ञ क्षेत्र का इतना विवरण पर्याप्त होगा। इन्हीं अग्नियों आदि के निर्माण हेतु ही शायद शुल्व ज्यामिति और मापन अस्तित्व में आए थे। यहां यह कहना लाजिमी है कि विभिन्न शुल्व सूत्रों में कम-से-कम छः अग्नियों का उल्लेख है।
बौधायन में इन सभी को नाम सहित उल्लेख है जबकि मानव में 4 व अपस्तंब में 2 का उल्लेख है और कात्यायन में एक का भी उल्लेख नहीं है। इसी प्रकार से सूत्रों में तेरह प्रकार की चितियों का उल्लेख है (मानव में समस्त तेरह, बौधायन में सात, अपस्तंब में छः और कात्यायन में एक)। चितियां मूलतः बारह प्रकार की हैं। किंतु कई प्रकारों में एक से अधिक प्रकार सम्मिलित होते हैं। यदि इन्हें अलग-अलग गिना जाए तो चितियां अट्ठारह प्रकार की होंगी। बौधायन में एक को छोड़ शेष समस्त का उल्लेख है। जिसका नाम वहां नहीं है वह सुपर्णचिति है जो काल्पनिक पक्षी गरुड़ के आकार की होती है। अपस्तंब और मानव दोनों में ग्यारह-ग्यारह चितियों का उल्लेख है जबकि कात्यायन में एक का भी नहीं।
समस्त अनुष्ठानों में इस बात का ध्यान रखना होता है कि धर्मग्रंथों में निर्धारित नियमों का कठोरता से पालन किया जाए। तनिक-सा भी विचलन पूरे प्रयास को निष्फल या हानिकारक भी बना सकता है। विभिन्न वैदिक पंथों के श्रौतसूत्रों में निर्देश दिए गए हैं जिनका कड़ाई से पालन करना होता है। किन्तु अग्नि आदि के निर्माण के नियमों में एकरूपता नहीं है। उदाहरणार्थ, एक मत के अनुसार गार्हपत्य अग्नि वृत्ताकार होनी चाहिए जबकि एक अन्य मत के अनुसार इसे वर्गाकार होना चाहिए। अलबत्ता, आकृति कुछ भी हो मगर इसका आकार समान होना चाहिए -1 वर्ग व्यायाम (9216 वर्ग अंगुल)। आहवनिया अग्नि वर्गाकार होती है तथा दक्षिण अग्नि अर्द्ध-वृत्ताकार। किंतु इन दोनों का आकार समान होना चाहिए -
1 वर्ग व्यायाम। जैसा कि पहले बताया गया, महावेदी समद्विबाहु समलंब की आकृति में होती है। इसका आकार निम्नानुसार होता है: फलक 24 पद (या एक अन्य मतानुसार 24 प्रक्रम) लंबा, आधार 30 पद (या 30 प्रक्रम) और ऊंचाई 36 पद (या 36 प्रक्रम)। सूत्रभति वेदी भी इसी आकृति की होगी किन्तु इसका क्षेत्रफल महावेदी से एक तिहाई होगा।
इटें, ज्यामिति और प्रमेय
इसके बाद हम आते हैं ईंटों पर। ये ईंटें भी विभिन्न आकृतियों व आकारों की हैं। कुछ ईंटें सरलरेखीय होती हैं। जैसे तिकोन, चौकोन, पंचभुज व षट्भुज चौकोन में भी वर्ग, आयत, समांतर चतुर्भुज, समलंबक आदि विविध आकृतियों की ईंटें हो सकती हैं। कुछ ईंटें ऐसी भी होती हैं जो एक तरफ से वक्राकार होती हैं जबकि शेष तीन पक्ष सरल रेखीय होते हैं।
हर चिति की अपनी अनोखी शक्ल होती है किंतु प्रत्येक का क्षेत्रफल 7.5 वर्ग पुरुष (1,08,000 वर्ग अंगुल) होना चाहिए। इसके प्रत्येक प्रस्तर (परत) में 200 ईंटें होनी चाहिए और कुल पांच प्रस्तर होने चाहिए। अर्थात् प्रत्येक चिति में 1000 ईंटें होनी चाहिए - न एक कम, न एक ज्यादा। एक छोड़कर शेष समस्त चितियों की ऊंचाई घुटने (जानु) के बराबर होनी चाहिए। एक बार चिति का निर्माण हो जाने के बाद यदि यजमान एक और काम्येष्टि (किसी मनोकामना की पूर्ति के लिए दी जाने वाली बलि) करना चाहे तो उसे चिति के क्षेत्रफल में 1 पुरुष की वृद्धि करना होती है। इसी प्रकार से एक-एक मनोकामना के लिए एक-एक पुरुष बढ़ाते हुए चिति का क्षेत्रफल 101.5 पुरुष तक बढ़ाया जा सकता है।
इस सबके लिए निम्नलिखित बातों पर अच्छी पकड़ होनी चाहिएः
1. किसी दी गई रेखा को बराबर लंबाई के खण्डों में बांटना।
2. किसी दी गई सरल रेखा से समकोण बनाती दूसरी सरल रेखा खींचना।
3. एक ऐसा वर्ग बनाना जिसकी लंबाई दी गई है।
4. दी गई लंबाई-चौड़ाई का आयत बनाना।
5. दी गई भुजाओं व झुकाव के आधार पर समांतर चतुर्भुज बनाना।
6. विषमबाहु त्रिभुज बनाना।
7. दो बिंदुओं के बीच बने वृत्त का केन्द्र बिंदु पता लगाना।
8. दिए गए वृत्त के अंदर बनाए जा सकने वाले बड़े-से-बड़े वर्ग को बनाना।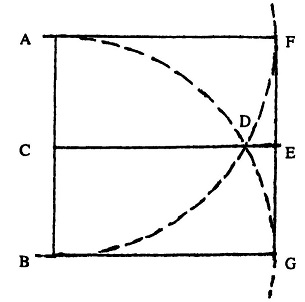 
वर्ग बनाने के तरीके
यहां स्थानाभाव के कारण हम इनमें से प्रत्येक प्रमेय की चर्चा नहीं कर पाएंगे। अतः हम एक समस्या (समस्या क्रमांक 3) को चुनकर उसकी चर्चा करेंगे। शुल्ब सूत्रों में वर्ग बनाने की एक-दो नहीं, पूरी पांच विधियां बताई गई हैं। संभवतः आपस्तंब में वर्णित विधि सबसे प्राचीन होगी। यह विधि निम्नानुसार है: "बांस की एक छड़ (वेणु) में दो छेद करें। इन दो छेदों के बीच उतनी ही दूरी हो जितनी दोनों भुजाएं उठाकर यजमान की ऊंचाई है। (अर्थात 1 पुरुष =120 अंगुल)। इन दो छेदों के बीचों-बीच एक तीसरा छेद कर दो। वेणु को पूर्व-पश्चिम रेखा (पृष्ट्या) पर रखकर उसके छिद्रों में शंकु लगा दो। अब पश्चिम की ओर के दो शंकु हटाकर वेणु को विपरीत छोर के छिद्र से उत्तर-पूर्वी दिशा में घुमाकर एक बृत्त बना लो। अब पूर्वी शंकु को हटाकर पश्चिमी छिद्र में शंकु लगाकर विपरीत छोर के छिद्र से दक्षिण-पश्चिम दिशा में वेणु को घुमाकर एक और वृत्त बना लो। अब वेणु को पूरी तरह स्वतंत्र करके पुनः इस तरह जमाओ कि सिरे का सुराख मध्य बिन्दु पर रहे। इसे दो वृत्तों के कटान बिन्दु पर दक्षिण की ओर रखो और सबसे बाहर के छिद्र के बिंदु पर एक शंकु लगा दो। इस शंकु पर वेणु का मध्य बिंदु जमाओ और वेणु को बृत्तों की परिधि पर जमा दो। अब बाहरी छिद्रों में एक-एक शंकु लगा दो। यही एक पुरुष की भुजा का वर्ग है।''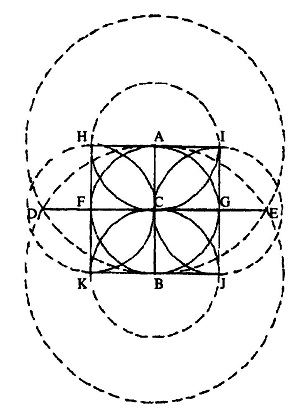
शुल्व की शब्दावली से नावाकिफ व्यक्ति के लिए तो यह कोई कूट संदेशसा है या किसी पेचीदा गुत्थी-सा है जिसे सुलझाया जाना है। किन्तु यदि हम इस वक्तव्य का यूक्लिड की समतल ज्यामिति की परिचित भाषा में 'तर्जुमा कर दें तो पूरी क्रिया एकदम सीधीसादी नज़र आएगी। इस तरह ‘अनुवाद के बाद यह बात कुछ इस तरह कही जाएगी (चित्र-2):
"AB एक, सरल रेखा है और C इसका मध्य बिंदु है। इस पर एक वर्ग बनाया जाना है। A व B बिन्दुओं से AB त्रि के दो चाप बिपरीत दिशाओं में खींचो। ये चाप परस्पर D बिंदु पर काटते हैं। बिंदु C व D को
चित्र:2 बांस की खपच्ची की मदद से वीआरजी बनाने की एक विधि। जिसके तहत दी गयी त्रिज्या के दो चाप खींचकर वर्ग बनाते हैं।
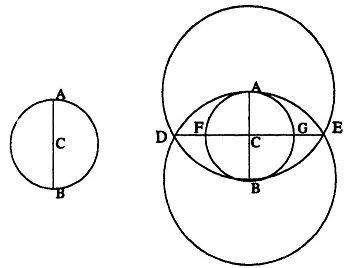
चित्र:3 रस्सी की मदद से वर्ग बनाने की एक विधि के शुरुआती चरण
चित्र:4 रस्सी की मदद से वृत खींचकर उनसे वर्ग बनाने की विधि का अंतिम चरण जिसमें वर्ग बन जाता है। आकृति स्पष्ट करने के लिए यह चित्र बड़ा करके दिखाया गया है।
जोड़ दो तथा D को बिन्दु E तक इस तरह आगे बढ़ाओ कि CE = ABI बिन्दु F ब 7 को इस तरह जोड़ो कि सरल रेखा FG बिन्दु E से होकर गुजरे। AF और BG को जोड़ दो। AFGB ही वांछित वर्ग है।"
आइए अब एक अन्य विधि देखते हैं जिसमें बांस की खपच्ची के स्थान पर रज्जु (रस्सी) का इस्तेमाल होता है। बौधायन शुल्बसूत्र के इस उद्धरण का अक्षरशः अनुवाद प्रस्तुत न करके हम यहां वर्तमान स्वरूप में उसका भावार्थ प्रस्तुत कर रहे हैं:
"AB एक सरल रेखा है जो वांछित वर्ग की एक भुजा की लंबाई के बराबर है। C इसका मध्य बिंदु है।c को केन्द्र मानकर तथा CA (=CB) को त्रिज्या मानकर एक वृत्त खींचो जो बिंदु A व B को स्पर्श करेगा। A और B को केन्द्र व AB को त्रिज्या मानकर दो और वृत्त खींचो। ये वृत्त एक-दूसरे को बिंदु D व E पर काटेंगे। (चित्र-3)
D E को इस तरह जोड़ो कि यह रेखा c से होकर गुजरे तथा दो वृत्तों को बिंदु F व G पर काटे।
अब चार वृत्त खींचो जिनकी त्रिज्या CA के बराबर हो तथा केन्द्र बिंदु क्रमशः A, B, F व G। ये चार वृत्त बिंदु H, I, J व K पर एक-दूसरे को काटेंगे। H I, II, JK और KH को जोड़ दो। HIJK ही वांछित वर्ग है।" (चित्र-4)
हम यह पहले ही कह चुके हैं कि अनुष्ठान हेतु बनी संरचनाएं अलगअलग आकृतियों में हो सकती थीं किन्तु इनका आकार (साइज़) एक ही होना चाहिए। इसके लिए एक सरल रेखीय आकृति को अन्य सरलरेखीय आकृति में बदलने और किसी वक्ररेखीय आकृति (खासकर किसी वृत्त) को समान क्षेत्रफल की सरल रेखीय आकृति में बदलने की क्षमता ज़रूरी है। उपरोक्त से विपरीत क्रिया भी करनी पड़ सकती है। इन क्रियाओं को निम्नांकित प्रमेयों का रूप दिया जा सकता है:
09. किसी आयत को बराबर क्षेत्रफल के वर्ग में बदलना।
10. किसी चतुरस्र (आयत या वर्ग) को बराबर क्षेत्रफल के त्रिभुज में बदलना।
11. किसी समद्विबाहु समलंब को बराबर क्षेत्रफल के वर्ग में बदलना।।
12. किसी समचतुर्भुज को बराबर क्षेत्रफल के वर्ग में बदलना।
13. किसी वर्ग को क्षेत्रफल में बराबर वृत्त में बदलना।
चतुर्भज से त्रिभुज बनाना
यहां भी हम कुछ चुनिंदा उदाहरणों पर ही चर्चा करेंगे। पहले हम समस्या क्रमांक 10 को लेते हैं अर्थात् चतुर्भुज को बराबर क्षेत्रफल के त्रिभुज में बदलना।
वर्ग का कर्ण AC खींचो और AC को एक भुजा मानकर ACEF वर्ग बनाओ। अब वर्ग की भुजा FA का मध्य बिंदु ज्ञात करो। GC व GE को जोड़ो। GCE ही वांछित समद्विबाहु त्रिभुज है। (चित्र-5)
यदि शुरुआत आयत से करनी हो तो पहले आयत को वर्ग में बदलना होगा और फिर शेष क्रिया उपरोक्तनुसार होगी।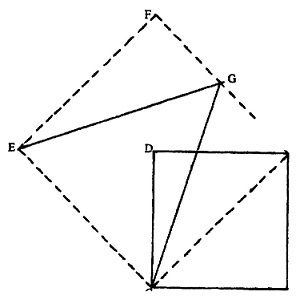
चित्र:5 चतुर्भुज को बराबर क्षेत्रफल के त्रिभुजों में बदलना। वर्ग का कर्ण AC खिंचों और AC को एक भुजा मानकर ACEF वर्ग बनाओ। अब वर्ग की भुजा FA का मध्य बिंदु ज्ञात करो। GC व GE को जोड़ो। GCE की वांछित समद्विबाहु त्रिभुज है।
इसका प्रमाण भी आसान है। चूंकि
AC = √2a (AB = a)
और त्रिभुज GCE की ऊंचाई
AC = √2a
और क्षेत्रफल
= 1/2 x √2a x √2a
= 1/2 x 2 a2 = a2 = वर्ग का क्षेत्रफल।
और प्रमेय 13 में प्रस्तुत समस्या को देखें। यह तो सर्वविदित है कि क्षेत्रफल समान रखते हुए किसी वृत्त को वर्ग में बदलना या वर्ग को वृत्त में बदलना स्केल और कंपास की मदद से संभव नहीं है। यानी यूक्लिड ज्यामिति की सीमाओं में इस समस्या को नहीं सुलझाया जा सकता। बौधायन शुल्बसूत्र में वर्णित विधि में भी एक सन्निकटन ही किया गया है हालांकि सन्निकटन हमें मनचाही स्थिति के बहुत करीब ले जाता है। विधि इस प्रकार है।
वृत्त का वर्ग
ABCD एक वर्ग है जिसकी भुजा a है। कर्ण AC खींचकर उसका मध्य बिंदु (O) ज्ञात कीजिए। अब 0 को केन्द्र तथा 0A को त्रिज्या मानकर चाप AB खींचिए। बिंदु E रेखा AB का मध्य बिंदु है। OE को जोड़ दीजिए और इसे F तक आगे बढ़ा दीजिए। EG=1/3 FE लेकर तथा 0 को केन्द्र व 0G त्रिज्या मानते हुए एक वृत्त GRSP खींचिए। यही वांछित वृत्त है। (चित्र-6)
आइए इसका प्रमाण देखें:
r(वृत्त GRSP की त्रिज्या) =OG =OE + EG
नोट : निम्नलिखित आर्टिक्ल मे पाई का चिन्ह, वर्गमूल संबन्धित चिन्ह एवं घातें नहीं प्रदशित की गईं हैं। (त्रुटि के लिए खेद)
= (a )/( 2 )+ EF/3
= a/( 2 )+ (OF-OE )/3
= a/( 2 )+ 1/( 3 )(√2/2× a -a/( 2 ))
[OF= OA= √2/2 a]
= a (1/( 2 )+1/(3√2)-1/( 6 ))
= a × 2((√2+1)/(6√2))
= a × ((√2+1)/(3√2))
अब √2 का मान 1.4142135 और पाई = 22/7 लें तो वृत का क्षेत्रफल होगा :
πr2 = 22/7×a2 ×((√2+1)/( 3√(2 )))
= a2×22/7 ((3+2√2))/18
= a2×11/( 63 ) (3+2×1.4142135.....)
= a2×11/( 63 ) (5.828427.....)
= a2×64.112697/63
= a2×1.017661857.....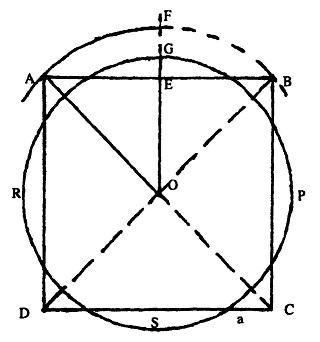
हम कुछ ऐसे प्रमेय और प्रतिपादित कर सकते हैं जिनमें नई संरचना की आकृति वही होगी किन्तु क्षेत्रफल अलग होगा।
14. किसी दिए गए वर्ग से दुगने क्षेत्रफल का वर्ग बनाना। ।
15. दिए गए वर्ग से तिगुने क्षेत्रफल का वर्ग बनाना।
16. किन्हीं दो वर्गों के क्षेत्रफल के योग के बराबर क्षेत्रफल का वर्ग तैयार करना।
17. किन्हीं दो वर्गों के क्षेत्रफल में अंतर के बराबर क्षेत्रफल का वर्ग तैयार करना।
आइए प्रमेय 16 को देखें। इसके संदर्भ में बौधायन के निर्देश अत्यंत स्पष्ट व कामकाजी हैं। (देखिए चित्र 7)
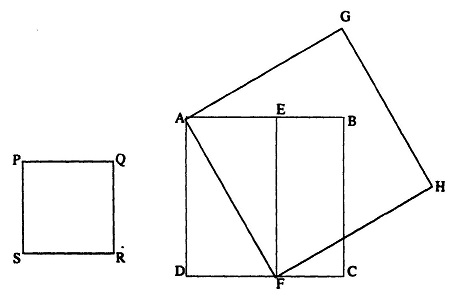
बड़े वर्ग में छोटे वर्ग की भुजा के बराबर एक आयताकार टुकड़ा काटो। इस आयत का कर्ण सम्मिलित वर्ग (अर्थात वांछित वर्ग) की भुजा होगी। आधुनिक ज्यामिति की भाषा में इसे कुछ इस तरह लिखा जाएगाः
माना कि ABCD बड़ा और PQRS छोटा वर्ग है। PQ के बराबर AE और DF काटिए। बिन्दु E को F से तथा A को F से जोड़िए। वर्ग AGHF खींचिए। वर्ग AGHF क्षेत्रफल में ABCD व PQRS के क्षेत्रफल के योग के बराबर है।
और अब चर्चा करते हैं ऐसी आकृतियों के निर्माण की जो क्षेत्रफल में किसी अन्य आकृति के बराबर हों।
18. दी गई भुजाओं वाला एक ऐसा समद्विबाहु समलम्ब बनाना जिसका क्षेत्रफल दिए गए वर्ग या आयत के बराबर हो।।
19. एक ऐसा समान्तर चतुर्भज बनाना जिसका क्षेत्रफल किसी वर्ग या आयत के बराबर हो।
20. दो पंचभुजों के समतुल्य वर्ग बनाना।
वर्ग के बराबर समद्विबाहु समलंब
हम यहां प्रमेय 18 की चर्चा करेंगे। माना कि ABCD एक वर्ग है और समलम्बक की भुजा PQ दी गई है। PQ की लम्बाई AB से कम है। (देखिए चित्र-8)
बिन्दु A ब D को केन्द्र तथा PQ को त्रिज्या मानते हुए दो चाप खींचिए जो AB व DC को क्रमशः बिन्दु R व 5 पर काटें। RS व RC को जोड़ दीजिए।
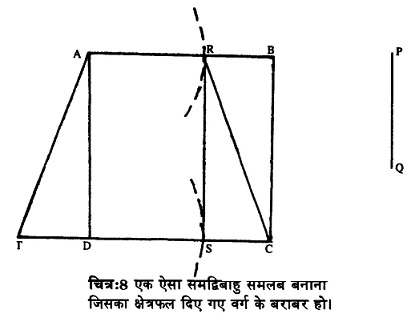
समकोण त्रिभुज RCS लेकर, उसे पलटाकर AD पर रख दीजिए। एक त्रिभुज ADT बनेगा और ARCT इच्छित समलम्बक होगा।
त्रिभुज RCS को पलटाने की क्रिया आसानी से की जा सकती है। रेखा CD को T तक बढ़ाइए ताकि DT=SC हो। अब बिन्दु A और T को जोड़ दीजिए। ARCT समलम्बक तैयार है। इसका प्रमाण स्वतः स्पष्ट है।
चार शुल्बसूत्रों से इस तरह के अन्य प्रमेय भी बनाए जा सकते हैं और वे भी कम रोचक न होंगे। किन्तु अब हम उक्त रचनाओं को बनाने में लगने वाली ईटों पर ध्यान देंगे। दरअसल ये ईंटें ही शुल्व सूत्रों की ज्यामिति और मापन को आकर्षक बनाती हैं। अग्नियों, बेदियों व चितियों के निर्माण में ईंटों की जरूरत होती है। यदि हम चितिनिर्माण से शुरू करें तो अधिक रुचिकर होगा। हम विभिन्न चितियों के नाम तो बता ही चुके हैं और उनमें से कुछ की आकृतियां भी दर्शा चुके हैं। अगले अंक में हम इन चितियों को एक साथ रखकर इनके विकास के क्रम को भी देखेंगे।
रामकृष्ण भट्टाचार्य: आनंद मोहन कॉलेज, कलकत्ता के अंग्रेजी विभाग में रीडर तथा कलकता विश्वविद्यालय में अंग्रेजी पाठ्यक्रम में अतिथि लेक्चरर। विज्ञान लेखन में रुचि।
अनुवाद : सुशील जोशीः एकलव्य के होशंगाबाद विज्ञान शिक्षण कार्यक्रम से जुटे हैं। साथ ही स्वतंत्र विज्ञान लेखन एवं अनुवाद करते हैं।