पुस्तक अंश
अन्य विषयों की तरह गणित को भी कक्षा में बेहतर ढंग से कैसे पढ़ाया जा सकता है जिससे बच्चों को गणित की पढ़ाई में मज़ा आए, कई शिक्षक यह जानना चाहते हैं। कई बार उनका सवाल होता है कि क्या विज्ञान की तरह गणित में भी कुछ ठोस गतिविधियां हो सकती हैं जिनकी मदद से गणितीय अवधारणाओं को बच्चे आसानी से समझ सकें? इस अंश में ऐसी ही कुछ गतिविधियों के बारे में जानकारी दे रहे हैं जिन्हें आपके आसपास मौजूद सामग्री से करवाया जा सकता है।
➔ शायद गणित पढ़ाने वाले सभी शिक्षकों के सामने एक सवाल खड़ा होता है मेरे छात्र गणित की परीक्षा में बेहतर कर सकें। इसके लिए मैं क्या कर सकता हूँ?
➔ बच्चे गणित को समझें और बेहतर तरीके से समझ सकें, इसके लिए गणित को भी गतिविधि आधारित होना चाहिए। गतिविधियां ऐसी जो सरल, सुलभ सामग्री पर आधारित हों।
➔ सामग्री या संसाधनों की बात आते ही हम-आप सोच में पड़ जाते हैं कि गणित के हिसाब से ऐसी कौन-सी सामग्री हो सकती है?
एक बात साफ उभरती है। संसाधनों और गतिविधियों के जरिए छात्र कहीं अधिक बेहतर तरीके से सीख सकते हैं। शिक्षक के दृष्टिकोण से जिन चीजों में कठिनाइयां आएंगी वे हैं आयोजन, काम की योजना और गतिविधियों का लगातार संचालन।
किन साधनों का उपयोग किया जा सकता है?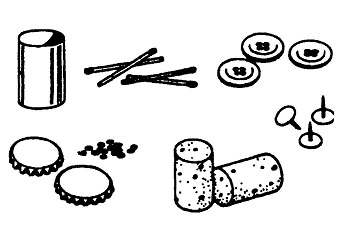
झाडू की मींकें, बोतलों के ढक्कन, कपड़े, माचिस की डिब्बियां, लिफाफे, मीपी-शंख, डोरियां, रबर के छल्ले, ड्राइंग पिने, मोती-मनके, छोटे पत्थर, फीते, बटन, सिक्के, बीज, डिब्बे और वर्तन, कपड़े मुखाने की रस्सी, अखबार, पुरानी पत्रिकाएं, कागज़ और पुराने कार्ड, छोटी डगालें, लकड़ी के टुकड़े, गत्ते के पुराने डिब्बे, काली मिट्टी, टीन, झोले, बोतलें और लोग। परन्तु इसमें सबसे आवश्यक और महत्वपूर्ण है, दिमाग। इनके अलावा कई और चीजें हैं जो आपको आसानी से स्कूल और स्थानीय परिवेश से मिल जाएंगी।
साधन तैयार करना
कुछ शैक्षिक साधनों को तैयार करने में देरी लगती है। परन्तु, उन्हें बार-बार इस्तेमाल किया जा सकता है। दूसरी ओर कुछ चीजें जल्दी बनाई जा सकती हैं और उन्हें भी बार-बार उपयोग किया जा सकता है। परन्तु कुछ वस्तुएं ऐसी हैं जिन्हें केवल एक ही बार इस्तेमाल कर सकते हैं। इनको बनाना चाहेंगे या नहीं, यह आप तय करें।
आपको कितनी संख्या में हरेक संसाधन चाहिए इसके बारे में भी सोचें। क्या आप इस मात्रा को कम कर सकते हैं? उदाहरण के लिए क्या आप, अपनी कक्षा का ढांचा बदल सकते हैं जिससे कि छात्रों का एक छोटा समूह ही एक बार में संसाधनों का प्रयोग करे? बाकी छात्र, सप्ताह के अन्य दिनों में उस उपकरण या शैक्षिक साधन को इस्तेमाल करें।
शिक्षण सामग्री आदि बनाने में सहायता लें। इसके लिए कुछ सुझाव इस प्रकार हैं: -
➔ छात्र अपनी कापियां खुद बना सकते हैं।
➔ गणित के क्लब में, छात्रों के साथ मिलकर सीखने के साधन बनाएं।
➔ अपने अन्य शिक्षक साथियों के साथ मिलकर शैक्षिक साधन बनाएं। धीरे-धीरे आपके पास शिक्षण सामग्री का एक बैंक बन जाएगा।
➔ स्थानीय कारीगरों आदि को शैक्षिक साधन बनाने के लिए स्कूल में बुलाएं।
➔ एक टाइम-टेबिल बनाएं। शिक्षा के हरेक सत्र में कुछ शैक्षिक साधन बनाएं। इस प्रकार कुछ समय बाद आपके पास संसाधनों का भी एक बैंक बन जाएगा।
मौका पड़ने पर संसाधन तुरंत उपलब्ध हों, इसके लिए उन्हें संभाल कर रखने की कोई जगह बनाएं। इसकी जिम्मेदारी किसी छात्र को सौंपे। छात्र सुनिश्चित करें कि ये साधन पूरी कक्षा में उपलब्ध रहें।
अगले कुछ पन्नों में हम गणित के उन शुरुआती बिन्दुओं के बारे में चर्चा करेंगे जिनमें, आसानी से बनाई इस शिक्षण सामग्री का इस्तेमाल हो सकता है।
बोतल के ढक्कनों का उपयोग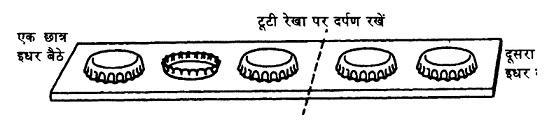 
विषय - प्रतिबिम्ब
दर्पण के एक ओर स्थित, हरेक बिन्दु का, दर्पण-रेखा के दूसरी ओर, उतनी ही दूरी पर प्रतिबिम्ब बनेगा।
आवश्यक सामानः बोतल के ढक्कन, छोटे दर्पण, कार्ड की पट्टी
गतिविधि
चित्र के अनुसार कार्ड की पट्टी पर बोतल के 5 ढक्कन रखें।
दर्पण को टूटी रेखा पर रखें। उसके दोनों ओर एक-एक छात्र बैठे। एक छात्र दूसरे से पूछे कि उसे क्या दिखाई दे रहा है? आपकी राय में, दूसरे छात्र को क्या दिखाई दे रहा होगा? अब दर्पण-रेखा को सरकाएं। अब आपको क्या दिख रहा है? दूसरे छात्र को क्या दिख रहा होगा?
ढक्कनों की दो कतारें बनाएं या भिन्न रंगों के ढक्कनों को, अलगअलग पैटर्न में सजाकर प्रयोग करके देखें।
विषय - अनुमान
नाप की किन्हीं भी दो इकाइयों की आपस में तुलना की जा सकती है। उदाहरण के लिए मीटर की तुलना सेंटीमीटर, इंच, हाथ के बालिश्त आदि से की जा सकती है।
गतिविधि
अनुमान के बारे में पूछताछ करने के लिए कक्षा में छात्रों की दो टीमें बनाएं। हरेक टीम, अनुमान से संबंधित प्रश्नों की एक सूची बनाए। उदाहरण के लिए: बोतल के कितने ढक्कनों से एक कप भरेगा? एक भगोना? एक बाल्टी? एक ट्रक? एक ट्रक बोतलों का भार कितना होगा?
बोतल के कितने ढक्कनों को सटाकर रखने से एक मीटर बनेगा? एक किलोमीटर? कक्षा की लंबाई?
हरेक टीम अपने प्रश्नों के उत्तरों के सही अंदाज़ की एक मान्य सीमा तय करे। जो टीम सबसे सही अनुमान लगाएगी, वही जीतेगी।
विषय - निर्देशांकों की जोड़ियां और रूपांतरण
➔ निर्देशांकों की जोड़ी किसी चौखाने के जाल में, जोड़ों की स्थिति को निरूपित करती है। जिस बिन्दु के निर्देशांक (2,3) होंगे, वह मूल बिन्दु से X अक्ष आड़ी रेखा) की तरफ 2 इकाई और Y अक्ष (खड़ी रेखा) की ओर 3 इकाई दूर होगा।
➔ रूपांतरण में किसी नियम के आधार पर, आकृतियों को बदलना और उन्हें स्थानांतरित करना होता है। आकृतियों को रूपांतरित करने के चार तरीके हैं: परावर्तन, घुमाना, स्थानांतरण और बड़ा करना।
निर्देशांकों के साथ गतिविधि
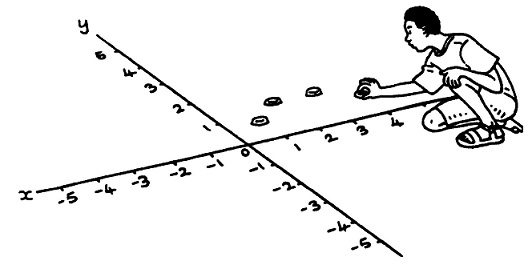
एक बड़े कागज पर या जमीन पर दो अक्षों को बनाएं। उन पर X और Y अक्ष लिखें।
चौखाने जाल पर बोतल के चार ढक्कनों को इस तरह रखें जिससे वे किसी चतुर्भुज के चार कोनों को निरूपित करें। उनके निर्देशांक नोट करें। इसी प्रकार कुछ अन्य चतुर्भुज बनाएं और उनके भी निर्देशांक नोट करें।
इन चतुर्भुजों को अलग-अलग समूहों में रखें जैसेः
वर्ग, आयत, समचतुर्भुज, समानांतर चतुर्भुज, पतंग, समलंब। हरेक समूह की निर्देशांक जोड़ियों में समानता खोजने का प्रयास करें।
रूपांतरण के लिए गतिविधियां
परावर्तन: दर्पण के एक ओर स्थित, हरेक बिन्दु का दर्पण-रेखा के दूसरी ओर, उतनी ही दूरी पर स्थित, प्रतिबिम्बित बिन्दु बनेगा। बोतल के 4 ढक्कनों की चपटी सतहें ऊपर रखकर, उनसे एक चतुर्भुज बनाएं। उनके निर्देशांक नोट करें। अब 4 ढक्कनों की दंतीली सतहें ऊपर रखकर, उनसे x अक्ष के दूसरी ओर पहले चतुर्भुज का प्रतिबिम्ब बनाएं। उनके भी निर्देशांक नोट करें। अब पहले चतुर्भुज और प्रतिबिम्बित चतुर्भुज के निर्देशांकों की तुलना करें।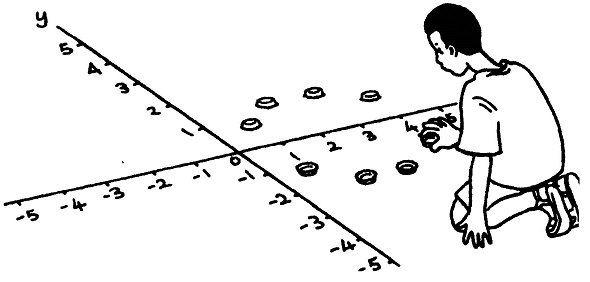
इस प्रयोग को कई अन्य चतुर्भुजों के साथ भी दोहराएं। उनके निर्देशांकों को नोट करें और फिर निर्देशांकों की जोड़ियों के बीच परस्पर सम्बंधों की जांच-पड़ताल करें। रेखा X= 0 और Y=X की रेखाओं से भी चतुर्भुजों को प्रतिबिम्बित करें।
घूमना: सभी बिन्दु केन्द्र के चारों ओर, एक-समान कोण से घूमेंगे।
ढक्कनों की चपटी सतहें ऊपर रखकर कोई आकार बनाएं। आकार के कोनों के निर्देशांकों को नोट करें। अब ढक्कनों की दंतीली सतहें ऊपर रखें और पहले आकार का मूलबिन्दु से घड़ी की दिशा में 90 डिग्री घूमा हुआ प्रतिबिम्ब बनाएं। इस नए प्रतिबिम्ब के निर्देशांक भी नोट करें। फिर दोनों निर्देशांक जोड़ियों की तुलना करें।
इसी प्रकार आकार को घड़ी की दिशा में 180 डिग्री और घड़ी की विपरीत दिशा में 90 डिग्री घुमाकर देखें।
बड़ा करना: कोई भी आकार किसी पैमाने के अनुसार ही बड़ा होता है। यह पैमाना ही निश्चित करेगा कि नए आकार की हरेक भुजा, कितनी बड़ी होगी।
ढक्कनों की चपटी सतह ऊपर रखकर कोई आकार बनाएं। आकार के कोनों के निर्देशांकों को नोट करें। अब ढक्कनों की दंतीली सतहें ऊपर रखें और मूलबिन्दु से, पहले आकार से दो गुनी बड़ी आकृति बनाएं। इस नई आकृति के निर्देशांकों को भी नोट करें। फिर दोनों निर्देशांक जोड़ियों की तुलना करें।
इसी प्रकार मूलबिन्दु से कुछ अन्य आकृतियों को दो गुना बड़ा करें। इनके नए निर्देशांकों को नोट करें। नए निर्देशांकों की जोड़ियों की आपस में तुलना करें।
इसी प्रकार 5, 1/2, -2 गुना बड़ा करने का प्रयास करें। अब मूलबिन्दु की बजाए अन्य बिन्दुओं से भी बड़ा करने की कोशिश करें।
स्थानांतरण: आकृति पर स्थित सभी बिन्दु एक ही दिशा में एक-समान दूरी तक ही सरकेंगे।
ढक्कनों की चपटी सतहें ऊपर रखकर, कोई आकार बनाएं। आकार के कोनों के निर्देशांकों को नोट करें।
अब ढक्कनों की दंतीली सतहें ऊपर रखकर, उसी आकार को, स्थानांतरित स्थिति में बनाएं। नई स्थिति के निर्देशांकों को भी नोट करें। फिर दोनों निर्देशांक जोड़ियों की तुलना करें।
भिन्न-भिन्न आकृतियों को स्थानांतरित करें। हर बार निर्देशांक नोट करें और फिर निर्देशांकों की जोड़ियों के बीच, परस्पर सम्बंधों को खोजें।
अब अलग-अलग प्रकार से स्थानांतरण करें और देखें कि क्या होता है। 
संयोग
सभी संभावित परिणामों की सूची बनाएं और उन्हें एक व्यवस्थित तरीके से गिनें।
गतिविधि
आप तीन भिन्न ढक्कनों को कितने अलग-अलग तरीकों से एक सीधी रेखा में सजा सकते हैं?
अलग-अलग संख्याओं के ढक्कनों के साथ इस प्रयोग को दोहराएं।
विषयः विकास के पैटर्न, अंकगणितीय श्रेणियां और ज्यामितीय श्रेणियां
विकास के पैटर्न में एक क्रम होता है जिसके अनुसार उनमें हर बार एक निश्चित बढ़त होती है।
बीजगणित के द्वारा इस बढ़त का वर्णन किया जा सकता है।
अंकगणितीय श्रेणियों के हर अंक में समान बढ़त होती है।
ज्यामितीय श्रेणियों के हर अंक में पहले की अपेक्षा कहीं अधिक बढ़त होती है। 
गतिविधि
बोतल के ढक्कनों से पैटर्न 1 बनाएं।
हरेक पैटर्न में कितने ढक्कन लगे? हर बार कितने और ढक्कन जोड़े गए?
नीचे की तालिका में, हर पद के लिए ढक्कनों की संख्या को गिनें:
पद 1:1 पद 2:1+... पद 3:1+... +... पद 4:1+...+...+...
nवें पद के लिए बीजगणित का नियम लिखें।
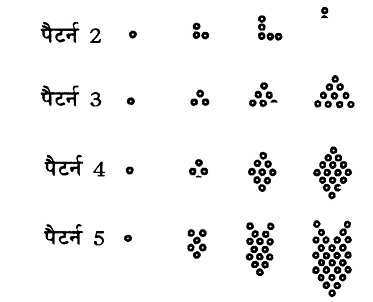
नीचे कई पैटर्न दिए गए हैं। उन्हें ढक्कनों से बनाएं। हरेक पैटर्न के लिए मालूम करें किः
➔ हरेक पद के लिए ढक्कनों की संख्या?
➔ हरेक पद पर, कितने और ढक्कन जोड़े गए?
हर बार की बढ़त को, बीजगणितीय नियम का रूप दें।
पांचवें पद, आठवें पद और 7वें पद में, लगने वाले ढक्कनों की संख्या लिखें। हरेक श्रेणी, अंकगणितीय होगी या ज्यामितीय, इसे तय करें। खोजबीन के लिए खुद ही इस प्रकार के कुछ पैटर्न बनाएं।