 सुशील जोशी
सुशील जोशी
सामान्यतः यह समझा जाता है कि वायुमंडलीय दबाव वायुमंडल के उस स्वतंत्र वज़न की वजह से होता है जो हमारे ऊपर कई किलोमीटर की ऊंचाई तक मौजूद है। इस व्याख्या पर सवाल उठाता है यह लेख। अगर हवा के कण एक-दूसरे के संपर्क में ही नहीं हैं तो वे वजन कैसे डाल सकते हैं हमारे ऊपर....... !!
साथ ही वायुमंडलीय दबाव को समझने के लिए वैकल्पिक रूप से गैसों के अणु गति सिद्धांत के द्वारा प्रयास किया गया है।
सोचा तो था कि गैसों के अणु गति सिद्धांत की बात करूंगा मगर जब इधर-उधर पढ़ना शुरू किया तो लगा कि पहले इस वायुमंडल को समझना जरूरी है। दरअसल अणु गति सिद्धांत यानी कायनेटिक मॉलिक्यूलर थियरी की बात ही वायुमंडल के दबाव के कारण उठी थी।
तमाम पुस्तकें देखीं तो पता चला कि सभी में यह लिखा है कि पृथ्वी के आसपास हवा का एक ओवरण है जो अपने वज़न के कारण धरती पर (तथा धरती की हर चीज़ पर) दबाव डालता है। किसी-किसी ने इसी बात को ‘मुक्त गिरने के त्वरण' (एक्सलरेशन ऑफ फ्री फॉल) का परिष्कृत नाम भी दिया है। काफी सहज ढंग से बताया गया है कि हवा पर गुरुत्वाकर्षण बल लगता है, इस वजह से उसमें भार होता है और यह भार धरती पर पड़ता है; यही वायुमंडलीय दबाव है। 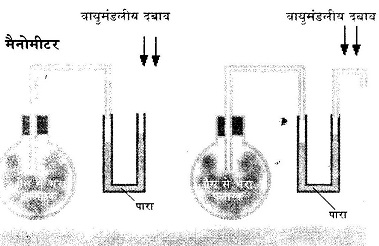 शुरुआती सवाल
शुरुआती सवाल
यह बात मेरे साधारण अनुभवों से मेल नहीं खाती। जैसे - जब मैं खुले आसमान के नीचे खड़ा हूं तब तो माना जा सकता है कि दूर तक फैले वायुमंडल का वज़न मेरे सिर पर टिका है। मगर जब मैं अपने घर की छत के नीचे बैठा हूं, तब? क्या मेरे ऊपर मात्र छत के नीचे की हवा का भार ही नहीं है? तो क्या घर के अन्दर और बाहर वायुमंडल का दबाव अलग-अलग है?
एक और उदाहरण देखिए। एक बोतल है, मुंह खुला है। इसके अंदर भी वायुमंडल फैला हुआ है। अब इस बोतल को उल्टा कर दिया। अन्दर की हवा का दबाव कितना होगा?
एक उपकरण होता है मैनोमीटर। इससे किसी भी पात्र में भरी गैस का दबाव नापा जा सकता है। एक नली में पारा भरा है। एक ओर से नली खुली है और वायुमंडल के संपर्क में है। दूसरी ओर नली को उस पात्र से जोड़ते हैं जिसकी गैस का दबाव पता करना है। यदि गैस का दबाव वायुमंडल के बराबर है तो नली में दोनों ओर पारे का तल बराबर रहेगा। मगर यदि गैस का दबाव ज्यादा है तो पारा दूसरी ओर की नली में थोड़ा ऊपर रहेगा। अब मान लीजिए वायुमंडल वाली नली को घुमाकर उसका मुंह नीचे की ओर कर दें।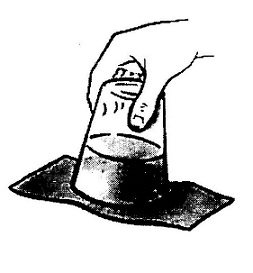 अब क्या होगा? यदि वायुमंडल का दबाव हवा के वज़न की बदौलत है तो अब यह दबाव तो शून्य हो जाना चाहिए (आखिर वज़न नामक बेल तो गुरुत्वाकर्षण के कारण है जो सदा नीचे की ओर काम करता है)। मगर यह पहले जितना ही रहता है।
अब क्या होगा? यदि वायुमंडल का दबाव हवा के वज़न की बदौलत है तो अब यह दबाव तो शून्य हो जाना चाहिए (आखिर वज़न नामक बेल तो गुरुत्वाकर्षण के कारण है जो सदा नीचे की ओर काम करता है)। मगर यह पहले जितना ही रहता है।
मुझे एक बात यह भी सिखाई गई थी कि हवा चारों ओर दबाव डालती है। यदि वायुमंडल का दबाव वज़न के कारण है तो दबाव सिर्फ नीचे की ओर ही लगना चाहिए। मगर निम्नलिखित प्रयोग बताते हुए सारी पाठ्य पुस्तकें इस बात को नकार देती हैं। आपने भी यह प्रयोग पढ़ा या करके देखा होगा। एक गिलास में पानी भर लें। गिलास के मुंह पर एक कागज़ लगा दें। कागज़ को हाथ से दबाकर रखें और गिलास को उल्टा कर दें। अब हाथ हटा लें। कागज़ नहीं गिरता। इसकी व्याख्या यह की जाती है कि हवा के दबाव के कारण कागज़ नहीं गिरता। मतलब हवा का दबाव नीचे से ऊपर की ओर भी लगता है! वैसे इस प्रयोग की यह व्याख्या सही नहीं है मगर जो पाठ्य पुस्तक लेखक इस पर भरोसा करते हैं उन्हें तो यह सोचना था कि वज़न कभी ऊपर की ओर नहीं लगता।
स्तंभ का वज़न कितना है?
अधिकांश किताबों में वायुमंडल के दबाव का एक आंकड़ा भी दिया जाता है। ऐसा बताते हैं कि समुद्र सतह पर धरती के प्रत्येक वर्ग सेंटीमीटर पर लगभग 1000 ग्राम वायुदाब है। इसे वे इस तरह व्यक्त करते हैं कि प्रत्येक वर्ग सेंटीमीटर के टुकड़े पर हवा का 1000 ग्राम का स्तंभ खड़ा है। मैंने सोचा कि यह पता किया जाए कि हमें यह आंकड़ा कहां से मिला। यह खोज बहुत रोचक साबित हुई।
बैरोमीटर एक यंत्र है जिसकी मदद से हम वायुमंडल का दबाव नापते हैं। पहले हमारे पास मात्र पारे के बैरोमीटर होते थे। इनकी बनावट बहुत ही आसान है। कांच की एक मीटर लंबी नली है जो एक सिरे से बंद है। इसमें ऊपर तक पारा भर देते हैं। अब उंगली से इसका मुंह बंद करके इसे पारा भरे बर्तन में उल्टा. खड़ा कर देते हैं। नली में से पारा गिरता है मगर पूरा नहीं गिरता। यदि प्रयोग समुद्र सतह के आसपास किया जाए तो नली में 76 सेंटीमीटर की ऊंचाई तक पारा बचा रहता है। यह पारा इसलिए नहीं गिरता क्योंकि बर्तन के पारे पर वायुमंडल का दबाव पारे को रोके रखता है। दबाव को हम प्रति इकाई क्षेत्रफल पर लग रहे बल के रूप में परिभाषित करते हैं। जैसे यदि 10 वर्ग सेंटीमीटर की सतह पर 10 किलोग्राम बल लगे तो उस सतह पर दबाव 10 किलोग्राम/10 वर्ग सेंटीमीटर = 1 किलोग्राम वर्ग सेंटीमीटर होगा।
यदि नली में 76 सेंटीमीटर की ऊंचाई तक पारा है तो प्रति वर्ग सेंटीमीटर सतह पर इसका वजन कितना होगा?
वज़न = आयतन X घनत्व
=76 सेंटीमीटर X 1 वर्ग सेंटीमीटर x 13.6 ग्राम/घन सेंटीमीटर
= 1030 ग्राम
यानी प्रति वर्ग सेंटीमीटर यह पारा 1030 ग्राम का बल लगा रहा है। इसे संभालने के लिए इतना ही बल वायुमंडल लगा रहा है। इसलिए कह दिया कि प्रति वर्ग सेंटीमीटर पर वायुमंडल के स्तम्भ का वजन करीब 1000 ग्राम है।
मैंने सोचा कि यह पता करें कि क्या वास्तव में वायुमंडल का 'वजन' इतना है। जितने भी आंकड़े मिले वे दरअसल इसी पारे की मात्रा के आधार पर गणना करके पता किए गए थे। जैसे ए.वी. ब्यालको की पुस्तक ‘अवर प्लेनेट - दि अर्थ' (मीर प्रकाशन) में बताया गया है कि धरती की सतह पर वायुमंडल का दबाव 1.01 3 x10° पास्कल है (1 पास्कल = 1 न्यूटन/वर्ग मीटर)। अब यह मानकर कि यह दबाव निश्चित रूप से गुरुत्वाकर्षण के कारण है', ब्यालको ने गणना करके बताया है कि हमारे वायुमंडल का वज़न 5.3x1018 किलोग्राम है। तो वायुमंडल का वजन आपको पारे के स्तंभ से ही मिलता है। मैंने सोचा कि क्यों न वास्तविक आंकड़ों के आधार पर यह गणना की जाए कि एक सेंटीमीटर क्षेत्रफल के वायुमंडल के बेलन का भार कितना होगा। इसके लिए आपको यह पता होना चाहिए कि वायुमंडल कितनी ऊंचाई तक है और उसका घनत्व क्या है। पहले यह पता करना था कि वायुमंडल की ऊंचाई कितनी है। यह सवाल आसान नहीं रहा। आप धरती की सतह से शुरू करें और ऊपर चलते जाएं तो आपको कहां तक हवा मिलेगी? सब कुछ पढ़ने के बाद लगता है कि हवा अनंत तक फैली हुई है - हां, इसका घनत्व जरूर कम होता जाता है। अब सवाल यह था कि घनत्व कितना कम हो जाने पर हम कहेंगे कि चलो अब वायुमंडल खत्म हुआ। यह तय करना इस बात पर निर्भर है कि आप किस मकसद से इस सवाल का जवाब पूछ रहे हैं। वह सवाल फिर कभी करेंगे। तो एक आंकड़ा मिला कि करीब 24 किलोमीटर की ऊंचाई पर वायुमंडल का घनत्व धरती की सतह पर वायु के घनत्व का मात्र 3 प्रतिशत रह जाता है। तो मैंने मान लिया कि वायुमंडल 24 किलोमीटर तक है।
मुझे यह पता है कि सामान्य ताप व दाब पर हवा के 22,400 मिली लीटर में एवोगैड्रो संख्या के बराबर अणु होते हैं। हवा में मुख्यतः नाइट्रोजन (78%) व ऑक्सीजन (21%) है। अतः हवा का एक औसत कण मानें तो 22,400 मिलीलीटर हवा का भार 29 ग्राम होगा। यानी प्रति घन सेंटीमीटर हवा का वज़न
29/22400 = 0.001 3 ग्राम होगा।
यदि 24 किलोमीटर ऊंचाई पर हवा का घनत्व शून्य मान लें, तो पूरे वायुमंडल में हवा का औसत घनत्व
0.0013/2 = 0.00065 ग्राम प्रति घन सेंटीमीटर है।
अब हम निकाल सकते हैं कि एक सेंटीमीटर आड़ी काट वाले 24 किलोमीटर (24,00,000 सेंटीमीटर) के वायु स्तंभ का वज़न क्या होगा।
24,00,000 x 0.00065 = 1560 ग्राम
यानी धरती की सतह पर प्रत्येक वर्ग सेंटीमीटर के टुकड़े पर 'वजन' 1560 ग्राम है, 1000 ग्राम नहीं।
अब बस यह देखना शेष है कि कहीं घनत्व का उपरोक्त आंकड़ा भी दबाव के आधार पर की गई गणना का परिणाम तो नहीं था। यदि संदर्भ के पाठकों में से कोई जानता हो तो ज़रूर बताए।
परन्तु यह भी संभव है कि मैं हवा के बेलन की लंबाई के बारे में, उसके घनत्व के क्रमशः रैखिक रूप से कम होते जाने आदि के बारे में जो मान्यताएं लेकर चला हूं उनकी वजह से यह अंतर आ रहा हो। शायद एकदम सटीक आंकड़े लेने पर हो सकता है कि एक सेंटीमीटर क्षेत्रफल पर खड़े हवा के वायुमंडलीय बेलन का वज़न लगभग 1000 ग्राम ही आ जाए।
फिर भी यह तो मानना ही पड़ेगा कि चूंकि हवा के कण एक-दूसरे के संपर्क में हैं ही नहीं इसलिए वे उस तरह से वज़न डाल ही नहीं सकते जैसे ठोस या द्रव के कण वज़न डालते हैं जो एक-दूसरे से सटे हुए हैं, एक-दूसरे के संपर्क में हैं।
अगर वायुमंडल का दबाव वायु स्तंभ के वज़न की वजह से नहीं है तो फिर इस दबाव की उत्पत्ति कहां है?
क्यों होता है गैसों का दबाव?
.... अभी तक मैंने यह बताने की कोशिश की थी कि गैसों का दबाव उनके वजन की वजह से नहीं होता। मैंने जितनी भी किताबें देखीं उन सबका यही कहना है कि वायुमंडल का दबाव उसके वज़न के कारण है। यहां तक कि कुछ किताबों में तो खासतौर पर स्पष्ट किया गया है कि गैस का दबाव और वायुमंडल का दबाव दो अलग-अलग चीजें हैं। अलबत्ता मुझे कोई कारण समझ में नहीं आता कि ऐसा क्यों होना चाहिए। इसलिए मैं अपनी बात को आगे बढ़ाऊंगा, जिसमें यह समझाना भी जरूरी होगा कि वायुमंडल का दवाव सिर्फ नीचे की ओर नहीं लगता बल्कि चारों दिशाओं में लगता है।
दरअसल गैसों की समझना काफी मुश्किल रहा था। काफी पहले ही रॉबर्ट बॉयल ने यह पताकर लिया था कि दबाने पर गैसें दबे जाती हैं और उनका दबाव बढ़ जाता है। यह भी पता चल गया था कि गर्म करने पर गैसें खूब फैलती हैं - खूब यानी ठोस और द्रव के मुकाबले कहीं ज्यादा। मगर ऐसा सब क्यों होता है? इस व्यवहार की व्याख्या के लिए पदार्थों का कण सिद्धांत सामने आया था। दरअसल गैसों का कण सिद्धांत परमाणु सिद्धांत से पहले ही उभर चुका था। इसी का एक विशेष मामला है गैसों का कण गति सिद्धांत।
कण ग़ति सिद्धांत
यह सिद्धांत कुछ बहुत ही सरल मान्यताओं का संग्रह है। इन मान्यताओं के आधार पर हम गैस के सारे गुणों की व्याख्या कर सकते हैं। वैसे इस सिद्धांत में लगातार नई-नई बातें जुड़ती रही हैं मगर इसकी मूल मान्यताएं नहीं बदली हैं।
1. सारे पदार्थ कणों से मिलकर बने हैं।
2. गैसों के कण एक-दूसरे से बहुत, दूर-दूर होते हैं। इतने दूर कि इनमें परस्पर कोई संपर्क नहीं होता।
3. गैसों का कुल आयतन उनके कणों के कुल आयतन की तुलना में बहुत ज्यादा होता है - इतना ज्यादा कि गैसों के कणों के वास्तविक आयतन को नगण्य माना जा सकता है।
4. गैसों के सारे कण तमाम अलग-अलग वेग से तमाम दिशाओं में लगातार गति करते रहते हैं।
5. गति करते हुए ये कभी-कभी आपस में भी टकराते हैं और बर्तन की दीवारों से भी। मगर ये टक्करें पूरी तरह लचीले ढंग से होती हैं। - यानी टक्कर के दौरान कणों की ऊर्जा का कोई ह्रास नहीं होता।
बस यही है गैसों का कण गति सिद्धांत। इस सिद्धांत के मुताबिक जब गैस के कण बर्तन की दीवार से टकराते हैं तो दीवार पर बल आरोपित होता है और यही बल दबाव के रूप में नज़र आता है।
दबाव = बल/क्षेत्रफल
यानी गैसों का दबाव उसके कणों द्वारा बर्तन पर मारी गई टक्कर के दौरान लगे बल के कारण उत्पन्न होता है।
अब चाहें तो गणित कर लें या मात्र तर्क के सहारे बात कर लें। जैसे, चूंकि कणों के बीच भरपूर खाली जगह है (मान्यता 2 व 3) इसलिए गैसों को खूब दबाया जा सकता है, खाली जगह ही तो है। इसके विपरीत ठोस व द्रव के कणों के बीच ज्यादा जगह नहीं होती, इसलिए दबाव बढ़ाने पर उनका आयतन बहुत नहीं बदलता।
मान्यता 4 के मुताबिक गैसों के कण अलग-अलग दिशाओं में भटकते रहते हैं। किसी कण का वेग बहुत अधिक हो सकता है, तो किसी का बहुत कम। गणनाओं को आसान बनाने के लिए हम अक्सर एक औसत वेग की बात करते हैं। औसत वेग बहुत अलग-अलग होते हैं। यदि सारे कणों के वेग देखेंगे तो उनका वितरण बेतरतीब यानी रैंडम होगा। अधिकांश कणों का वेग औसत के आसपास होगा जबकि कुछ कणों को इससे बहुत कम और कुछ का इससे बहुत ज्यादा होगा।
| कण गति सिद्धांत के आधार पर गैस का वजन एक वेब साइट पर गैस के वज़न की गणना इस तरह बताई गई है। गैस का वज़न न्यूटन के नियम से ज्ञात हो सकता है, बशर्ते कि गैस के कणों के बीच सारी टक्करें पूरी तरह लचीली हों। पहले किसी एक कण को लेते हैं। यह किसी भी दिशा में जा सकता है। मान लीजिए इसकी गति का एक घटक y दिशा में है। तो देर सबेर यह बर्तन की ऊपरी और निचली दीवार से टकराएगा। इस कण का वेग V0 है और मात्रा m है। एक दीवार से दूसरी दीवार तक जाने में इसे समय लगता है। जब यह ऊपरी दीवार से टकराएगा तब टकराने से पहले इसका संवेग mv0 होगा और टकराने के बाद -mv0 यानी संवेग में परिवर्तन mv0- (-mv0) = 2mv0 होगा। इतना परिवर्तन प्रति 2t समय में होगा। यानी बर्तन की ऊपरी दीवार पर लगने वाला औसत बल Ftop = 2mv0/2t है। अब यह कण नीचे की ओर जाना शुरू करता है। नीचे की ओर इस पर गुरुत्वाकर्षण बल g लग रहा है, तो इसकी गति बढ़ती जाएगी। निचली दीवार तक पहुंचने में यदि इसे t समय लगता है तो टकराने से पूर्व इसकी गति Vb=V0+ tg हो जाएगी। तब वहां संवेग परिवर्तन होगा mv0 - (- mvb) = 2mvb = 2m (v0+tg) = 2mv0 + 2mtg यह संवेग परिवर्तन भी 2t समय में होता है। तो निली दीवार पर लगने वाला औसत बल Fbottonm = (2mv0 + 2mtg)/2t होगा। बलों में अंतर Fbottonm - Ftop = (2mv0) + 2mtg)/2t - 2mvo/2t = mg यानी इन दो बलों के बीच का अंतर ही गैस के कणों का वज़न है। यह गणना हमने एक अणु के लिए की है मगर सारे अणुओं का मामला भी यही रहेगा। इस बात से भी कोई अंतर नहीं पड़ना चाहिए कि प्रत्येक कण ऊपर-नीचे की दीवारों से टकराने से पहले बीच में कितने कणों से टकराता है। इस गणना का अर्थ क्या है? क्या गैस का दबाव नीचे की ओर ज्यादा होता है? |
तापमान, आयतन और दबाव
अब मान लीजिए इस गैस को ऊष्मा दी गई। ऊष्मा एक तरह की ऊर्जा है। यह ऊर्जा पाकर गैस के कणों का वेग बढ़ेगा। एक नया वितरण स्थापित होगा जिसमें कणों का औसत वेग पहले से ज्यादा होगा (मगर फिर भी कुछ कण बहुत ज्यादा, कुछ बहुत कम वेग पर रहेंगे)। चूंकि कणों का औसत वेग बढ़ गया है इसलिए अब दीवार के साथ उनकी टक्कर भी ज्यादा जोर से होगी, संवेग का स्थानांतरण भी ज्यादा होगा। प्रति सेकेंड दीवार से टकराने वाले कणों की संख्या भी बढ़ जाएगी। इन दोनों वजहों से दबाव बढ़ जाएगा। यदि गैस का तापमान बढ़ाया जाए और आयतन वही रखा जाए तो दबाव बढ़ जाएगा।
दूसरी स्थिति देखते हैं। गैस को दबाकर उसका आयतन कम किया जाए। जाहिर है अब गैस के उतने ही कण कम आयतन में हैं। गैसों के कण परस्पर या बर्तन की दीवार से टकराते हैं। प्रत्येक दो टक्करों के बीच जो औसत दूरी वे तय करते हैं उसे हम औसत मुक्त अंतराल (mean free path) कहते हैं। जब कम आयतन में उतने ही कण हैं तो औसत मुक्त अंतराल कम हो जाएगा। वे जल्दी-जल्दी दीवार से टकराएंगे, लिहाजा दबाव बढ़ जाएगा।
तीसरी स्थिति देखते हैं। गैस को ऊष्मा दी जा रही है मगर उसे फैलने की गुंजाइश भी दी जा रही है - बर्तन की एक दीवार ऐसी है कि जो आगे-पीछे सरक सकती है। ऊष्मा मिलने से गैस के कणों की गतिज ऊर्जा बढ़ रही है, उनका औसत वेग भी बढ़ रहा है। वे अपनी तेज रफ्तार के कारण बर्तन की दीवार पर ज्यादा संख्या में और ज्यादा जोर से टकराएंगे; जिससे सरक सकने वाली दीवार थोड़ी सरक जाएगी और बर्तन का आयतन बढ़ जाएगा। मगर इसका मतलब यह भी होगा कि उनके बीच की खाली जगह और भी ज्यादा हो जाएगी। अब कण दीवार पर ज्यादा जोर से टक्कर मारेंगे मगर टक्करों की कुल संख्या कम हो जाएगी। तो कुल मिलाकर अंततः दबाव नहीं बढ़ेगा।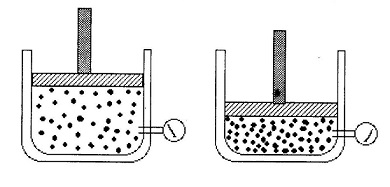 अब इस सिद्धांत के आधार पर वायुमंडल को देखना चाहता हूं। अभी तक हमने गुरुत्वाकर्षण की बात नहीं की है। मगर उसे नजर अंदाज करना संभव नहीं है। गैस के कण इधर-उधर भटकते हुए गुरुत्वाकर्षण से मुक्त नहीं हैं। दरअसल वायुमंडल इस गुरुत्वाकर्षण के कारण ही टिका हुआ है। प्रत्येक कण पर पृथ्वी अपना आकर्षण बेल लगा रही है। हमने देखा था कि इन कणों का वेग बेतरतीब ढंग से वितरित है - परिमाण में भी और दिशा में भी। किसी भी समय कुछ कण इतनी तेज़ गति में होते हैं कि वे पृथ्वी से दूर जाते हैं। हां, ऐसा नहीं है कि वे एक सीधी रेखा में जाते चले जाएंगे। बीच-बीच में वे दूसरे कणों से टकराते हैं। जब वे टकराते हैं तो उनकी गति की दिशा बदल जाती है। दो कणों की टक्कर के दौरान तेज चाल से चलते कणों में ऊर्जा का ह्रास हो सकता है। और उनकी चाल धीमी पड़ सकती है। (परन्तु टक्कर के पहले और बाद, दोनों कणों की कुल ऊर्जा में कोई बदलाव नहीं होगा।) इस तरह वे आड़े-तिरछे भागते हैं। इस बे-तरतीबी में कुछ कण पृथ्वी के पास और कुछ कण पृथ्वी से दूर निकल जाते हैं। चूंकि किसी भी तापमान पर वेगों का एक सामान्य वितरण होता है इसलिए अधिकांश कण पृथ्वी के निकट रहते हैं। जैसे-जैसे हम पृथ्वी से दूर जाएंगे गैसों के कणों की तादाद कम होती जाएगी। आखिर, गुरुत्व बल के विरुद्ध उतने ऊपर टिके रहने के लिए काफी अधिक वेग चाहिए, जो अपेक्षाकृत कम कणों को मयस्सर होता है। इस बेतरतीब स्थिति में यदि किसी कण की गति पलायन वेग (escape velocity) से अधिक हो तो वह हमें सदा के लिए अलविदा भी कह सकता है।
अब इस सिद्धांत के आधार पर वायुमंडल को देखना चाहता हूं। अभी तक हमने गुरुत्वाकर्षण की बात नहीं की है। मगर उसे नजर अंदाज करना संभव नहीं है। गैस के कण इधर-उधर भटकते हुए गुरुत्वाकर्षण से मुक्त नहीं हैं। दरअसल वायुमंडल इस गुरुत्वाकर्षण के कारण ही टिका हुआ है। प्रत्येक कण पर पृथ्वी अपना आकर्षण बेल लगा रही है। हमने देखा था कि इन कणों का वेग बेतरतीब ढंग से वितरित है - परिमाण में भी और दिशा में भी। किसी भी समय कुछ कण इतनी तेज़ गति में होते हैं कि वे पृथ्वी से दूर जाते हैं। हां, ऐसा नहीं है कि वे एक सीधी रेखा में जाते चले जाएंगे। बीच-बीच में वे दूसरे कणों से टकराते हैं। जब वे टकराते हैं तो उनकी गति की दिशा बदल जाती है। दो कणों की टक्कर के दौरान तेज चाल से चलते कणों में ऊर्जा का ह्रास हो सकता है। और उनकी चाल धीमी पड़ सकती है। (परन्तु टक्कर के पहले और बाद, दोनों कणों की कुल ऊर्जा में कोई बदलाव नहीं होगा।) इस तरह वे आड़े-तिरछे भागते हैं। इस बे-तरतीबी में कुछ कण पृथ्वी के पास और कुछ कण पृथ्वी से दूर निकल जाते हैं। चूंकि किसी भी तापमान पर वेगों का एक सामान्य वितरण होता है इसलिए अधिकांश कण पृथ्वी के निकट रहते हैं। जैसे-जैसे हम पृथ्वी से दूर जाएंगे गैसों के कणों की तादाद कम होती जाएगी। आखिर, गुरुत्व बल के विरुद्ध उतने ऊपर टिके रहने के लिए काफी अधिक वेग चाहिए, जो अपेक्षाकृत कम कणों को मयस्सर होता है। इस बेतरतीब स्थिति में यदि किसी कण की गति पलायन वेग (escape velocity) से अधिक हो तो वह हमें सदा के लिए अलविदा भी कह सकता है।
इसी सिलसिले को आगे बढ़ाएं। मान लीजिए कहीं गैस का दबाव कम हो जाए। यह दो कारणों से हो सकता है। या तो वहां गैस के कणों की औसत गति धीमी पड़ जाए या कुल कणों की ‘संख्या कम हो जाए। मजेदार बात यह है कि ये दो स्थितियां, दो परस्पर विरोधी कारणों की वजह से हो सकती हैं - खासकर वायुमंडल के मामले में। इसका कारण यह है कि वायुमंडल एक खुला तंत्र है। उसकी कोई ऊपरी सीमा नहीं है। आमतौर पर यदि गैस किसी बरतन में भरी है और उसका तापमान बढ़ाया जाए तो गैस के कणों की औसत गति तेज़ हो जाएगी। इसके परिणामस्वरूप गैस का दबाव बढ़ जाएगा। यह इसलिए क्योंकि हमने उसका आयतन स्थिर रखा है। मगर वायुमंडल में ऐसा नहीं है। गर्म होकर वायुमंडल फैल सकता है। जब कणों की औसत गति बढ़ती है तो अपेक्षाकृत अधिक कणों का वेग इतना होगा कि वे पृथ्वी से ज्यादा दूर बने रह सके। तब प्रति इकाई आयतन में कणों की संख्या अपेक्षाकृत कम हो जाएगी।
ध्यान दें कि मैं यह सुझा रहा हूं कि जब किसी स्थान पर तापमान बढ़ता है तो वहां वायुमंडल फैलता है। और ज़ाहिर है वहां उसकी ऊंचाई बढ़ जाती है। (एक बात और देखने की है। यदि हवा का दबाव वजन के कारण होता है तो उस हवा के फैलने से दबाव में कोई कमी नहीं आनी। चाहिए थी - यदि हम वायुमंडल का एक बेलनाकार स्तंभ घेरकर अलग कर दें ताकि उसका फैलाव आड़ी दिशा में नहीं सिर्फ खड़ी दिशा में हो सके तो आखिर फैले या सिकुड़े, वज़न थोड़े ही बदलेगा।) ऐसे स्थानों पर हवा के ज्यादा कण ऊपर की ओर उठते हैं। गौरतलब बात यह है कि इस स्थिति में भी कई कणों का वेग औसत से काफी कम होगा और वे नीचे की ओर आएंगे। मगर बड़ी संख्या में कणों की गति का सांख्यिकीय वितरण (Statistical Distribution) देखेंगे तो ज्यादा कण ऊपर की ओर उठेंगे। इसी को हम कहते हैं कि हवा गर्म होकर ऊपर उठती है। यह कथन मात्र एक सांख्यिकीय वितरण दर्शाता है। इसका मतलब यह नहीं है कि हवा एक ठोस वस्तु की तरह तैरकर ऊपर चली जाती है।
हवा या गैस के कणों की गति तो हर तरफ चलती रहती है। हवा के कण क्षैतिज दिशा में भी भटकते रहते हैं। जब किसी स्थान पर हवा बिल्कुल नहीं चल रही हो तब भी हवा के कण लगातार इधर-से-उधर भटकते रहते हैं। मगर इस स्थिति में किसी स्थान पर कणों की संख्या कम हो जाए तो वहां से बाहर जाने वाले कणों की संख्या कम होती है और बाहर से वहां आने वाले कणों की संख्या अधिक हो जाती है। तब ऐसा लगता है कि हवा वहां भागी चली आ रही है। ध्यान देने की बात यह है कि इस समय भी कुछ कण ज़रूर ऐसे होंगे जो धारा के विरुद्ध जा रहे होंगे। एक बार फिर, यह सांख्यिकीय वितरण का सवाल है। ज्यादातर कण एक ही दिशा में जा रहे हैं - मगर अभी भी हर कण एक-दूसरे से स्वतंत्र विचरण कर रहा है। इसी को हम कहते हैं कि जब हवा गर्म होकर ऊपर उठती है तो आसपास की हवा उसका स्थान लेने वहां आ जाती है - आंधी का रूप भी ले सकती है।
कुल मिलाकर कहने का मतलब यह है कि हवा के बहाव (चाहे नीचे-ऊपर या दाएं-बाएं) का सूक्ष्म चित्र काफी पेचीदा हो सकता है। जब सांख्यिकीय वितरण ऐसा हो कि अधिकांश कण एक ही दिशा में भाग रहे हों तो स्थूल चित्र से काम चल सकता है।
अभी तक हमने पांच बातें की हैं जो इस प्रकार हैं:
1. हवा का दबाव उसके वजन के कारण नहीं होता बल्कि उसके कणों द्वारा किसी भी सतह पर मारी गई टक्करों की वजह से होता है।
2. दबाव में परिवर्तन दो वजह से हो सकता है - कणों के वेग में परिवर्तन के कारण और कणों के घनत्व में परिवर्तन के कारण। (यहां यह बात ध्यान देने की है कि कणों का घनत्व और गैस का स्थूल घनत्व दो अलग-अलग चीजें हैं। जैसे कार्बन डाईऑक्साइड का एक अणु ऑक्सीजन के एक अणु से करीब 1.4 गुना भारी होता है। मगर यदि किसी बर्तन में इन दोनों के बराबर कण लिए जाएं तो दोनों का कण घनत्व बराबर होगा। इस स्थिति में दोनों का दबाव बराबर होगा, बशर्ते कि वे एक समान तापमान पर हैं।)
3. तापमान बढ़ाने पर कणों का औसत वेग बढता है. इसकी वजह से या तो गैस फैल सकती है या उसका दबाव बढ़ सकता है।
4. गैसों का एक स्थान से दूसरे स्थान तक जाना उन दो स्थानों पर कणों के घनत्व पर निर्भर होता है। इसे दूसरे शब्दों में यूं भी कह सकते हैं कि यह स्थानांतरण दो स्थानों के दबाव पर निर्भर है क्योंकि दबाव कण-घनत्व पर निर्भर है।
5. स्थूल रूप में देखें तो हवा एक स्थान से दूसरे स्थान तक जाती हुई मानी जा सकती है मगर सूक्ष्म चित्र कहीं ज्यादा पेचीदा होता है। - कण दोनों दिशाओं में जाते हैं। मगर परिणामी गति एक दिशा में होती है।
इसके बाद कण गति सिद्धांत के आधार पर दबाव की गणना की जा सकती है। कण गति सिद्धांत के आधार पर गैस के वज़न की एक व्याख्या यहां प्रस्तुत है।
वैसे एक सवाल सामने रखकर बात अधूरी छोड़ना चाहता हूं - यदि हमारे वायुमंडल में गैसों की प्रतिशत मात्रा बदल जाए तो वायुमंडलीय दबाव बदलेगा या नहीं? जैसे यदि वायुमंडल में कार्बन डाईऑक्साइड की मात्रा वर्तमान 0.03 प्रतिशत से बढ़कर 5 प्रतिशत हो जाए तो?
सुशील जोशीः एकलव्य द्वारा प्रकाशित स्रोत फीचर सेवा से जुड़े हैं। विज्ञान लेवन और विज्ञान शिक्षण में रुचि।



