प्रज्ञा कदम
माध्यमिक स्तर की गणित की कक्षाओं में चांदे, परकार, सेट स्क्वेयर, पेंसिल, रबर जैसे साधनों की मदद से विविध ज्यामितीय आकृतियों की रचना के अभ्यास करवाए जाते हैं। इन रचनाओं का निर्माण करते हुए कोई सवाल उठाने, तर्क करने, नया तरीका खोजने, अपनी परिभाषाएँ गढ़ने आदि के लिए कोई जगह नहीं होती।
गणित की शिक्षिका - प्रज्ञा कदम का मानना है कि यदि बच्चों को मौके दिए जाएँ तो बच्चे विषयवस्तु के साथ प्रयोग कर सकते हैं और ज्ञान निर्माण भी करते हैं। आइए पढ़ते हैं गणित शिक्षण के उनके अनुभवों को।
अपने एम.एड. कोर्स के एक हिस्से के रूप में मैंने यह तय किया कि उच्च माध्यमिक स्कूलों के छात्रों को ‘ज्यामितीय आकृतियों’ के बारे में पढ़ाऊँगी।
‘ज्यामितीय आकृतियों’ का विषय कक्षा-5 से 10 तक गणित के पाठ्यक्रम में शामिल है। किन्तु पाठ्यपुस्तकों में सिर्फ कुछ आकृतियों को बनाने के नुस्खे भर होते हैं और उनमें नवाचार करने या सवाल करने की कोई गुंजाइश नहीं होती। पाठ्यपुस्तकों में यह नहीं बताया जाता कि वही चरण क्यों अपनाए जा रहे हैं या वे चरण कैसे काम करते हैं।
दरअसल, मैं भी आकृति बनाने के सवाल इसी तरह से पढ़ाती आई हूँ जैसे मुझे पढ़ाया गया था: निर्माण के चरणों का प्रदर्शन करके। अपनी कक्षाओं में मुझे कभी यह महसूस नहीं हुआ कि किसी ज्यामितीय आकृति को बनाने के लिए निर्धारित विधि के कारण स्पष्ट करूँ। उम्मीद यही होती थी कि बच्चे उन चरणों को याद कर लेंगे और दोहराएँगे। इस परिस्थिति में होता यह था कि यदि बच्चों को कुछ दिनों बाद वही आकृति बनाने को कहा जाता, तो उन्हें कण्ठस्थ किए हुए चरण याद नहीं आते थे और वे उसे बना नहीं पाते थे। और तो और, यदि किसी नई ज्यामितीय आकृति से सामना हो जाता, तो खुद मैं भी उसे नहीं बना पाती थी।
किताबों और चर्चाओं से मैंने सीखा था कि ज्यामितीय आकृतियाँ बनाना ‘विशेष किस्म का तार्किक प्रमाण है जिसमें प्रारम्भिक आँकड़ों के आधार पर स्केल, परकार, सेट स्क्वेयर और चांदे की मदद से कुछ निश्चित संख्या में रेखाएँ और वृत्त बनाए जाते हैं और इस प्रक्रिया में नए कटान बिन्दु प्राप्त किए जाते हैं और अन्तत: वांछित आकृति प्राप्त होती है’।
इस परिभाषा से मुझे समझ में आया कि ये सवाल सूत्रविधि के सवाल नहीं हैं बल्कि प्रमाण हैं। इसका अर्थ है कि चापों के प्रत्येक कटान बिन्दु के पीछे एक तर्क है, रचना का तर्क है। तो मेरा काम यह था कि बच्चों के लिए रचना के सवालों को तार्किक प्रमाणों की तरह प्रस्तुत करूँ और इसमें एक मददगार की भूमिका निभाऊँ। बच्चों को ये प्रमाण स्वयं हासिल करने चाहिए।
इस व्यवस्थित प्रयास के लिए कक्षा-5, 6 व 7 के तीस छात्रों का एक विविध समूह चुना गया। अधिकांश स्कूलों में बच्चों को गणितीय प्रक्रियाओं (जैसे अटकल लगाना, बिम्ब निर्माण करना, परिकल्पना बनाना, अनुमान लगाना, चयन करना, डिज़ाइनिंग और योजना बनाना, योजना को क्रियान्वित करना, निर्णय लेना, व्यवस्थित करना या सवाल हल करना) में शामिल होने का शायद ही कोई मौका मिलता है। विचार यह था कि ज्यामितीय आकृतियों को एक औज़ार के रूप में इस्तेमाल करके बच्चों को इन प्रक्रियाओं में जोड़ा जाए।
मैंने तय किया कि बुनियादी ज्यामितीय आकृतियों पर काम करते हुए बच्चों को चतुर्भुजों की रचना का अनुभव दिया जाए। इनमें वर्ग, आयत, समचतुर्भुज (रोम्बस) और पतंग (एक चतुर्भुज जिसमें पास की दो भुजाएँ बराबर होती हैं) शामिल थे। इन चतुर्भुजों की विशेषता यह है कि इनके विकर्ण या तो एक-दूसरे को लम्बवत काटते हुए दो बराबर भागों में बाँटते हैं या कम-से-कम दो बराबर भागों में बाँटते हैं।
चूँकि बच्चों को कई किस्म के चतुर्भुज बनाने थे, इसलिए यह ज़रूरी था कि वे यह समझें कि चतुर्भुज क्या होता है। इसलिए मैंने सबसे पहले कालखण्ड में यह गतिविधि करवाई कि वे ‘चार भुजा वाली आकृति/बहुभुज’ के लिए यह नाम उपयोग करने लगें। (मैंने चार भुजा वाले बहुभुज के लिए ‘चतुर्भुज’ शब्द का उपयोग न करके उन्हें चार भुजा वाली आकृतियाँ कहा।) इस कालखण्ड की सारी गतिविधियाँ बच्चों ने समूहों में की। प्रत्येक समूह में पाँच-छ: बच्चे थे।
भाग 1: बच्चे परिभाषा बनाते हैं, परिभाषाओं को परिष्कृत करते हैं
जब मैंने बच्चों से चार भुजा वाली आकृति के लिए नाम सुझाने को कहा तो वे चक्कर में पड़ गए। उन्होंने कहा कि वे नहीं जानते कि उस गतिविधि में करना क्या है। तो मददगार के रूप में मैंने उन्हें एक उदाहरण दिया।
“यदि मैं ‘त्रिकोण’ कहूँ तो मन में कौन-सी आकृतियाँ आती हैं? ऐसी आकृति जिसमें तीन कोण हों। देखो, त्रिकोण में तीन कोण हैं, तीन भुजाएँ हैं, तीन शीर्ष हैं। तो हम तय करते हैं कि तीन कोण होने के कारण हम इसे ‘त्रिकोण’ कहेंगे।”
फिर मैंने समझाया, “इसी प्रकार से यदि तुम चार भुजा वाली आकृति को नाम देना चाहो तो सबसे पहले पता लगाओ कि उसमें कौन-कौन-से गुण हैं।”
पिछली कक्षा में बच्चों ने चार भुजा वाली आकृति के विभिन्न गुणधर्मों की एक सूची बनाई थी। मैंने उन्हें उन गुणों का उपयोग करने की सलाह दी।
लगभग 10 मिनट बाद बच्चों ने चार भुजा वाली आकृति के लिए विभिन्न नाम सुझाए। मैंने देखा कि समूह में काम करते हुए बच्चे एक-दूसरे के मत भी पता कर रहे थे।
पहले समूह के बच्चों ने नाम सुझाया ‘अन्तर्सम्बन्ध’ (interconnection)। जब कारण बताने को कहा गया तो उन्होंने समझाया कि यह आकृति चार कोणों को एक-दूसरे से जोड़कर बनती है।
मैंने तय किया था कि तुरन्त कोई प्रतिक्रिया नहीं दूँगी। तो मैंने यह उत्तर स्वीकार कर लिया।
दूसरे समूह ने नाम ‘समानान्तर चतुर्भुज’ (parallelogram) तय किया था। कारण समझाते हुए उन्होंने कहा कि वे यह नाम पहले से जानते थे, इसलिए उन्हें लगा कि चार भुजाओं वाली आकृति का यह एक नाम है।
तीसरे समूह के बच्चों ने ‘चतुर्भुज’ नाम दिया। उन्होंने बताया कि वे पहले से जानते थे कि चार भुजा वाली आकृति को ‘चतुर्भुज’ कहते हैं।
चौथे समूह ने नाम सुझाया था ‘चार समूह’ (four sets) और उन्होंने कारण यह बताया कि सारी चार भुजा वाली आकृतियों में चार भुजाएँ, चार कोण, चार शीर्ष होते हैं। इसलिए यह चार-चार चीज़ों के समूह से बनी होती है।
यह सही है कि दूसरे व तीसरे समूह के बच्चों ने अपने पूर्व-ज्ञान को याद करने की कोशिश की थी किन्तु चौथे समूह ने अपने अवलोकनों को पहले सीखी गई ‘समूह’ की अवधारणा से जोड़ने का प्रयास किया।
पाँचवे समूह ने नाम दिया ‘बिन्दुदार आकृति’ (Dotted shapes)। उन्होंने कारण दिया कि ये सारी आकृतियाँ बिन्दुओं से बनी हैं।
आखिरी समूह ने ‘चार-कोण’ (tetra-angle) नाम सुझाया और कारण यह बताया कि सारी चार भुजाओं वाली आकृतियाँ चार कोणों से बनी होती हैं इसलिए उन्हें tetra-angle कहा जा सकता है।
चौथे, पाँचवें तथा छठे समूह ने चार भुजा वाली आकृतियों का अवलोकन व विश्लेषण करके उसके आधार पर नाम सुझाने की कोशिश की।
सारे नाम सुनने के बाद कक्षा को इनमें से एक नाम चुनना था जिसका उपयोग वे नियमित रूप से करेंगे। इसके लिए उन्हें प्रत्येक समूह द्वारा सुझाए नाम की खूबियाँ और कमज़ोरियाँ ढूँढ़नी थीं।
‘अन्तर्सम्बन्ध’ (interconnection) नाम के बारे में अन्य समूह के सदस्यों का कहना था कि यह नाम नहीं माना जा सकता क्योंकि कोण वास्तव में जुड़े नहीं हैं बल्कि उन्हें रेखाओं से जोड़ा गया है।
‘समानान्तर चतुर्भुज’ नाम को खारिज कर दिया गया क्योंकि कक्षा-7 के अधिकांश बच्चे जानते थे कि यह एक विशेष किस्म का चतुर्भुज होता है, इसलिए सारी चार भुजा वाली आकृतियों के लिए लागू नहीं किया जा सकता।
‘चतुर्भुज’ (quadrilateral) नाम को भी बच्चों ने खारिज कर दिया। उनका कहना था, “यह नाम तो पहले से ही किताब में दिया है, हम तो ऐसा नाम चाहते हैं जो हमने दिया हो।”
‘बिन्दुदार आकृति’ नाम बच्चों ने यह कहकर खारिज कर दिया कि “बिन्दुओं के अलावा आकृति में कई और चीज़ें हैं।” ‘चार समूह’ (Four sets) नाम बच्चों को अस्वीकार था क्योंकि उसमें दो शब्द हैं। छात्रों के अनुसार उन्हें नाम के लिए एक शब्द चाहिए।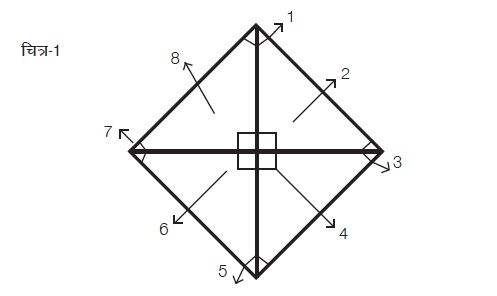
जब अपनी बात समझाने को कहा गया तो समूह के एक छात्र ने बोर्ड पर रेखाचित्र बनाकर दिखाया कि कैसे चार भुजा वाली आकृति आठ कोणों से बनी है (चित्र-1)।
कक्षा के अन्य बच्चों ने उसे समझाया कि हर शीर्ष पर एक कोण पर ही ध्यान दिया जा सकता है क्योंकि यही बात त्रिकोण के सन्दर्भ में देख सकते हैं। अन्तत: कक्षा में आम सहमति बन गई कि चार भुजा वाली आकृतियों को tetraangle कहेंगे।
इस सत्र में मैंने देखा कि हालाँकि पूर्व-ज्ञान और जानकारी बातचीत का एक बड़ा हिस्सा रही, किन्तु बच्चे नए विचार और नया ज्ञान गढ़ने को उत्सुक थे।
इस तरह की गतिविधि बच्चों को विषय से जोड़ने में मददगार हो सकती है क्योंकि विषयवस्तु वे स्वयं निर्मित कर रहे हैं। इसके अलावा वे यह भी समझ पाते हैं कि इस विषय की विषयवस्तु कैसे विकसित होती है।
चतुर्भुज की परिभाषा विकसित करने के बाद कक्षा विशेष tetra-angles (चतुष्कोणों) की परिभाषाएँ गढ़ने की दिशा में आगे बढ़ी।
यह एक आम एहसास है कि बच्चे अकेले काम करने के आदी होते हैं। अगली कक्षा के लिए मैंने भी यही योजना बनाई थी कि वे अकेले-अकेले काम करेंगे किन्तु जब मैं कक्षा में पहुँची तो वे पहले से ही समूहों में बैठे हुए थे। यह इस बात का संकेत हो सकता है कि उन्हें समूहों में काम करने में मज़ा आया था।
दो समूहों को ‘वर्ग’ की परिभाषा बनाने का काम दिया गया था। इसी प्रकार से दो समूहों को ‘पतंग’ और दो समूहों को ‘आयत’ की परिभाषा विकसित करने का काम दिया गया था। बच्चों को सम्बन्धित चतुर्भुजों के कट-आउट के अलावा एक-एक रंगोली कागज़ दिया गया था जिस पर विभिन्न किस्म के चतुर्भुजों की आकृतियाँ बनी थीं। इनके अलावा उन्हें वर्कशीट्स दी गई थीं जिनमें सम्बन्धित चतुर्भुज के गुणधर्म थे।
मैंने उनके साथ थोड़ी चर्चा यह समझने के लिए की कि उन्हें गतिविधि समझ में आई है या नहीं।
शिक्षक: तुमने गणित तथा कई विषयों में परिभाषाएँ देखी हैं। तो इन परिभाषाओं के बारे में तुम्हें क्या लगता है?
छात्र 1: परिभाषा एक वाक्य की होती है और वाक्य बहुत छोटा होता है।
छात्र 2: कभी-कभी वाक्य बहुत बड़ा भी होता है।
शिक्षक: उस वाक्य में होता क्या है?
छात्र: उस चीज़ के बारे में जानकारी।
शिक्षक: क्या उसमें सारी जानकारी होती है या कोई खास जानकारी?
छात्र: कोई खास जानकारी।
शिक्षक: कोई ऐसी कसौटी खोजो जो सारी परिभाषाओं में होनी चाहिए।
छात्रों ने आपस में चर्चा की और कुछ कसौटियाँ बताईं।
* उसमें एक वाक्य होना चाहिए।
* परिभाषा से हमें tetra-angle (चतुष्कोण) के सारे गुणधर्म मिल जाना चाहिए।
* गुणधर्मों को दोहराया नहीं जाना चाहिए।
बच्चों ने काम शुरु कर दिया। मैंने देखा कि यद्यपि वे समूह में बैठे थे मगर लगभग सारे बच्चे अपनी-अपनी परिभाषा बनाने की कोशिश कर रहे थे।
हमने तय किया कि हर किस्म के tetra-angle के लिए एक सर्वोत्तम परिभाषा चुनेंगे।
कुछ समय बाद बच्चों ने वर्ग की निम्नलिखित परिभाषाएँ खोजीं।
परिभाषा 1: वर्ग एक चार भुजाओं वाली आकृति होती है जिसकी सारी भुजाएँ बराबर होती हैं और पास-पास की भुजाएँ भी बराबर होती हैं जिसके चलते आमने-सामने की भुजाएँ समानान्तर होती हैं। इसमें सारे कोण बराबर बनते हैं और सम्मुख कोण भी बराबर होते हैं और अन्दर वाले कोण बराबर होते हैं।
परिभाषा 2: वर्ग एक चार भुजा वाली आकृति होती है जिसके सारे कोण 90 अंश के होते हैं।
परिभाषा 3: चार बराबर भुजा वाली आकृति जिसकी आमने-सामने की भुजाएँ बराबर होती हैं, और पास-पास की भुजाएँ भी बराबर होती हैं। विकर्ण एक-दूसरे के लम्बवत होते हैं। आन्तरिक कोण बराबर व पूरक होते हैं। और तो और, विकर्ण एक-दूसरे को दो बराबर भागों में बाँटते हैं और लम्बवत होते हैं।
परिभाषा 4: ऐसा tetra-angle (चतुष्कोण) जिसमें हर कोण 90 अंश का होता है, सारी भुजाएँ बराबर होती हैं और विकर्ण बराबर होते हैं और एक-दूसरे को दो बराबर भागों में बाँटते हैं।
परिभाषा 5: वर्ग एक काल्पनिक चार भुजा वाली ज्यामितीय वस्तु है जिसकी सारी भुजाएँ, कोण और विकर्ण बराबर होते हैं।
इन सारी परिभाषाओं को पढ़ने के बाद बच्चों ने अपने अभिमत दिए:
“पहली परिभाषा में कई सारे वाक्य और गुणधर्म हैं, इन्हें जोड़कर एक सामान्य गुणधर्म बनाया जा सकता है।”
“दूसरी परिभाषा में वर्ग के केवल एक गुणधर्म का उपयोग किया गया है, अन्य गुणधर्मों का उपयोग नहीं किया गया है। परिभाषा के लिए जिस गुणधर्म का उपयोग किया गया है, वह आयतों के लिए भी सही है और इसलिए यह वर्ग को नहीं दर्शाती।”
“तीसरी परिभाषा में सारे गुणधर्म बता दिए गए हैं। इन्हें जोड़कर एक छोटी परिभाषा बनानी चाहिए।”
बच्चों को चौथी परिभाषा पसन्द आई। उनका कहना था, “इसमें सारे ज़रूरी मूलभूत गुणों को शामिल कर लिया गया है।” बच्चों ने समूह द्वारा द्यड्ढद्यद्धठ्ठ-ठ्ठदढ़थ्ड्ढ (चतुष्कोण) शब्द के उपयोग को भी पसन्द किया। अन्य बच्चों ने भी महसूस किया कि वे भी चार भुजा वाली आकृति की बजाय इस शब्द का उपयोग कर सकते थे।
बच्चों को पाँचवीं परिभाषा भी अच्छी लगी क्योंकि इसमें कहा गया था कि ‘वर्ग एक काल्पनिक वस्तु है’। इसमें सारे ज़रूरी गुणधर्मों को भी शामिल किया गया था। पूरी कक्षा में चर्चा के बाद बच्चों ने वर्ग के लिए निम्नलिखित परिभाषा बनाई।
परिभाषा: वर्ग वह tetra-angle (चतुष्कोण) है जिसकी सारी भुजाएँ बराबर हों और सारे कोण बराबर हों।
यह तय किया गया कि हमारे आगे के काम के लिए इस परिभाषा का उपयोग किया जाएगा।
अगली गतिविधि पतंग की परिभाषा खोजने की थी। छात्रों ने जो परिभाषाएँ बनाईं, वे इस प्रकार थीं:
परिभाषा 1: ऐसे tetra-angle जिनमें विकर्ण भिन्न होते हैं और सिर्फ एक ही दूसरे को दो बराबर भागों में बाँटता है।
परिभाषा 2: ऐसा चतुष्कोण जिसमें पास-पास की भुजाएँ बराबर हों। विकर्ण असमान होते हैं और एक विकर्ण दूसरे को दो बराबर भागों में बाँटता है।
परिभाषा 3: पतंग एक ज्यामितीय आकृति है जिसकी चारों भुजाएँ गैर-बराबर होती हैं।
परिभाषा 4: ऐसा चतुष्कोण जिसमें एक जोड़ी कोण बराबर होते हैं और विकर्ण एक-दूसरे को दो बराबर भागों में बाँटते हैं।
इस गतिविधि में बच्चों ने अपना काम बाँट लिया था। उन्होंने सारे गुणधर्म एकत्रित करने का काम किसी एक बच्चे को सौंप दिया जबकि अन्य बच्चे परिभाषा बनाने की चर्चा में जुट गए। इस बार उन्होंने पतंग की जो परिभाषाएँ बनाईं, वे वर्ग की परिभाषा से कहीं ज़्यादा सटीक थीं। उन्होंने वर्ग की अपेक्षा इन परिभाषाओं को बनाने में समय भी कम लिया। बच्चों ने कम-से-कम शब्दों और वाक्यों का उपयोग करने की कोशिश की। चर्चा के अन्त में जो सामान्य परिभाषा निकली वह पाठ्यपुस्तक में दी गई परिभाषा के काफी नज़दीक थी। परिभाषा निम्नानुसार थी:
परिभाषा: ऐसा चतुष्कोण जिसमें सम्मुख कोणों की एक जोड़ी के कोण बराबर होते हैं और बड़ा विकर्ण छोटे को दो बराबर भागों में बाँटता है।
यहाँ बच्चों ने tetra-angle शब्द की बजाय चतुष्कोण (quadrangle) शब्द का उपयोग किया। मैंने उनसे इसका अर्थ समझाने को कहा, तो उन्होंने समझाया कि quadra का मतलब भी चार होता है, इसलिए हम tetra-angle की बजाय quadrangle का उपयोग कर सकते हैं।
यह स्पष्ट था कि अपना ज्ञान स्वयं निर्मित करने की जो आज़ादी मिली थी, बच्चे उसका लुत्फ उठाने लगे थे। इससे उनमें स्वयं के द्वारा निर्मित ज्ञान को लेकर अधिकार का भाव पैदा होने लगा था।
हमारी कक्षाओं में परिभाषाएँ छात्रों को बता दी जाती हैं, उन पर बमुश्किल कोई बातचीत होती है। पाठ्यपुस्तकों में भी परिभाषा के प्रतिपादन को लेकर कोई चर्चा नहीं की जाती। पाठ्यपुस्तकों में परिभाषाएँ और गुणधर्म अलग-अलग दिए जाते हैं। हमारी कक्षाओं में इस बात पर शायद ही कोई चर्चा होती हो कि परिभाषा में उस अवधारणा के गुणधर्म समाहित होते हैं या कैसे अन्य गुणधर्म किसी परिभाषा में से व्युत्पन्न (डिराइव) किए जा सकते हैं।
भाग 2: समझ के साथ रचना
उन्हीं बच्चों के साथ एक अन्य सत्र में एक चतुर्भुज बनाने को कहा गया। इस गतिविधि के लिए बच्चों को कागज़ की पतली-पतली पट्टियाँ दी गई थीं (इनमें कुछ पट्टियाँ बराबर लम्बाई की और कुछ गैर-बराबर लम्बाई की थीं)। उनसे कहा गया कि इन पट्टियों का उपयोग करके वांछित चतुर्भुज बनाएँ।
एक समूह में बच्चों ने निम्नलिखित तरीके से वर्ग बनाया।
समूह के सदस्यों ने इसे बनाने की प्रक्रिया समझाई।
छात्र: सबसे पहले मैंने बराबर लम्बाई की चार पट्टियाँ लीं और आड़ी पट्टी के एक सिरे पर एक पट्टी को 90 अंश के कोण पर रखा, फिर तीसरी पट्टी को पहली आड़ी पट्टी के समानान्तर रखा और फिर आखिरी पट्टी को रखा।
शिक्षक: किस चरण में तुम्हें यकीन हो गया था कि बनने वाला tetra-angle (चतुष्कोण) वर्ग ही होगा?
छात्र: तीसरे चरण में क्योंकि उसके बाद मेरे पास यही विकल्प था कि चौथी पट्टी को पहली आड़ी पट्टी के लम्बवत रखूँ।
शेष समूहों ने भी निर्माण का यही तरीका अपनाया था किन्तु किसी भी समूह ने निर्माण की प्रक्रिया में वर्ग के विकर्णों के गुणधर्म पर ध्यान नहीं दिया था। ऐसा शायद इसलिए हुआ क्योंकि परिभाषा बनाते वक्त तो उन्होंने विकर्ण के गुणधर्मों पर गौर किया था किन्तु अन्तिम परिभाषा में यह गुणधर्म प्रतिबिम्बित नहीं हुआ था।
एक अन्य समूह के बच्चों ने एक रोम्बस (समचतुर्भुज) की रचना इस प्रकार की थी: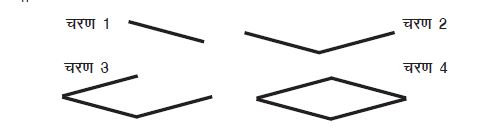
रोम्बस की एक अन्य रचना में निम्नलिखित चरणों का उपयोग किया गया था:
पतंग बनाने वाले एक समूह ने निम्नलिखित विधि अपनाई थी:
किसी अन्य समूह के सारे बच्चों ने पतंग को निम्नलिखित चरणों में बनाया:
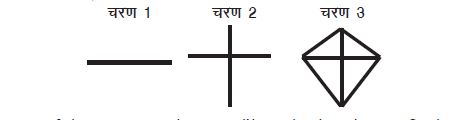
अगले सत्र में बच्चों से कहा गया कि वे ज्यामिति के उपकरणों और पेंसिल से कुछ चतुर्भुज बनाएँ (जिन्हें वे पिछले सत्र में बना चुके थे)।
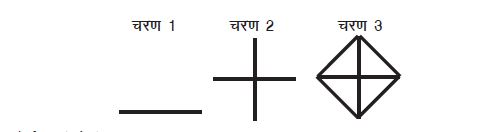
पहले समूह के बच्चे वर्ग बना रहे थे, उन्होंने सिर्फ स्केल का उपयोग किया। आकृति बनाते समय उन्होंने यह तो ध्यान रखा कि सारी भुजाएँ बराबर हों, किन्तु कोण के गुणधर्म का ख्याल रखना भूल गए। जब मैंने उनके द्वारा बनाए गए वर्ग को नापने को कहा तो पता चला कि उस आकृति में कुछ कोण 90 अंश के नहीं हैं। जब उन्हें समझ में आया कि यह तरीका काम नहीं कर रहा है तो उन्होंने वह विधि याद करना शु डिग्री की जो नियमित गणित कक्षा में पढ़ाई गई थी। कुछ देर बाद सातवीं कक्षा की एक बच्ची ने निम्नलिखित आकृति बनाई।
मेरे ख्याल में ऐसा इसलिए हुआ होगा क्योंकि वर्ग को आम तौर पर निम्नांकित ढंग से दर्शाया जाता है।

पतंग बनाने वाले बच्चों के समूह ने निम्नलिखित विधि बताई।
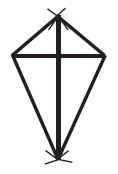
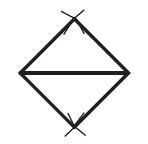
एक अन्य समूह ने रोम्बस बनाया। इस समूह के एक छात्र ने इसका प्रदर्शन किया।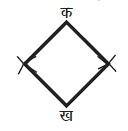
छात्र 2: यह मेरी विधि के समान ही है। मैंने पहले क्षैतिज रेखा बनाई और फिर उर्ध्वाधर रेखा। यहाँ उसने पूरा उर्ध्वाधर रेखाखण्ड नहीं बनाया है, सिर्फ रेखाखण्ड के अन्तिम बिन्दु चिंहित कर दिए हैं।
छात्र 1: मुझे पता था कि रोम्बस को पहले आड़ी रेखा खींचकर बनाया जा सकता है। किन्तु मैं एक नई विधि विकसित करना चाहती थी।
इसी समूह के एक अन्य छात्र (कक्षा-7) ने रोम्बस को निम्नलिखित तरीके से बनाया।
कक्षा-5 के एक छात्र ने रोम्बस निम्नलिखित तरीके से बनाया: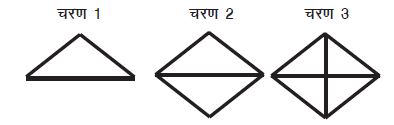
मैंने पूछा, “तुमने अपने समूह के अन्य साथियों के समान लम्बवत समद्विभाजक का उपयोग क्यों नहीं किया?” उसने बताया, “मुझे उनकी विधि तो पहले से पता थी। मैं अपना तरीका बनाना चाहता था।”
इस छात्र ने वास्तव में एक वर्ग बनाया था (जो रोम्बस भी है) किन्तु वह यह बात समझ नहीं पाया था। दरअसल, कक्षा में किसी भी छात्र ने उसे वर्ग के रूप में नहीं पहचाना था। कारण वही हो सकता है जिसकी चर्चा पहले की गई थी कि बच्चे बर्फी के आकार को रोम्बस और डिब्बे के आकार को वर्ग मानते हैं। इसलिए यह ज़रूरी है कि शिक्षक कक्षा में इस बात पर ज़ोर दे कि वर्ग भी रोम्बस ही होता है। शिक्षक को इसे आड़े और खड़े रूप में बनाकर भी दिखाना चाहिए। और तो और, प्राथमिक कक्षाओं में भी शिक्षक को चाहिए कि वह वर्ग को विभिन्न दिशाओं में रखकर बनाए ताकि यह बात स्पष्ट हो कि कोई आकृति उसके कोणों और भुजाओं के आधार पर वर्ग होती है, न कि इस आधार पर कि वह दिखती कैसी है।

उपरोक्त चर्चा से स्पष्ट है कि मौका मिले तो बच्चे विषयवस्तु के साथ प्रयोग कर सकते हैं, अवधारणा में अपनी सूझबूझ जोड़ सकते हैं और ज्ञान पैदा कर सकते हैं। उन्हें अपने तरीके, आकृतियों के नाम, अवधारणाओं की परिभाषाएँ विकसित करना अच्छा लगता है। यदि ज्ञान का निर्माण उनके द्वारा किया जाता है तो उनके, शिक्षक के और विषय के बीच का फासला गायब हो जाता है। मैं मानती हूँ कि सीखने-सिखाने का यह तरीका काफी समय की माँग करता है जो स्कूलों में इन अवधारणाओं के लिए आवंटित समय से ज़्यादा है। किन्तु अपने अनुभव से मैं कह सकती हूँ कि समय के साथ जब बच्चे अपने सीखने की ज़िम्मेदारी स्वयं उठाने के आदी हो जाते हैं तो सीखने की रफ्तार तेज़ हो जाती है।
प्रज्ञा कदम: पिछले 12 सालों से मुम्बई के विभिन्न पब्लिक स्कूलों में गणित की शिक्षिका रही हैं। स्कूली बच्चों को गणित पढ़ाने और सीखने में विशेष रुचि।
सम्पादन: आलोका कान्हरे।
अँग्रेज़ी से अनुवाद: सुशील जोशी: एकलव्य द्वारा संचालित स्रोत फीचर सेवा से जुड़े हैं। विज्ञान शिक्षण व लेखन में गहरी रुचि।