कॉन्सटेंस कामी
अभी तक हमने यह दर्शाने की कोशिश की कि बच्चों को अंकगणित के नियमों की खोज स्वत: करनी चाहिए क्यूँकि (1) तार्किक-गणितीय ज्ञान एक ऐसा ज्ञान है जिसकी रचना अपनी स्वयं की सोच से हर एक बच्चा कर सकता है व उसे करनी चाहिए। (2) आज की कलन-विधियों (algorithms) को समझने के लिए ज़रूरी है कि बच्चे हमारे पुरखों की ही तरह उस रचनात्मक प्रक्रिया से गुज़रें जिनसे ये कलन-विधियाँ उपजी हैं। एक तीसरी वजह जिसके चलते हम यह कहते हैं कि बच्चों को सवाल हल करने के अपने तरीके स्वयं खोजने चाहिए वो यह है कि नीचे दी गई तमाम वजहों के चलते ये कलन-विधियाँ प्राइमरी स्तर पर बच्चों पर अपना दुष्प्रभाव छोड़ जाती हैं:
- कलन-विधियाँ बच्चों को अपनी सोच छोड़ देने के लिए बाध्य करती हैं।
- स्थानीय मान से दूर ले जाकर बच्चों को संख्याओं की एक समग्र समझ बनाने में बाधक होती हैं।
- वे बच्चों को संख्याएँ लिखने की विशेष व्यवस्था (या पेपर-पेंसिल) व अन्य लोगों पर निर्भर बना देती हैं।
आगे हम इकट्ठी की गई जानकारी प्रस्तुत करते हुए इन तीनों बिन्दुओं पर विस्तार से चर्चा करेंगे।
बच्चों का अपनी गणितीय सोच को छोड़ना
जब बच्चों को कलन विधि (सवालों को हल करने की नियमों की प्रणाली) सीधे-सीधे ना सिखाकर उन्हें खुद अपने तरीके खोजने के लिए प्रोत्साहित किया जाता है तब उनकी सोच सिखाई जाने वाली विधि से अलग दिशा में जाती है। मिसाल के तौर पर जोड़ने, घटाने व गुणा करने की तमाम सिखाई जाने वाली विधियाँ दाएँ से बाएँ की ओर जाना सिखाती हैं, वहीं बच्चों के शुरुआती तमाम प्रयास हमेशा बाएँ से दाएँ की दिशा में होते हैं। वहीं विभाजन सिखाने की विधियाँ बाएँ से दाएँ की तरफ बढ़ती हैं, लेकिन तीसरी कक्षा के बच्चे की अपनी सोच हमेशा दाएँ से बाएँ की दिशा में होती है। चित्र-1 में इन चारों गणितीय क्रियाओं के बच्चों द्वारा खोजे गए उदाहरणों को दर्शाया गया है।
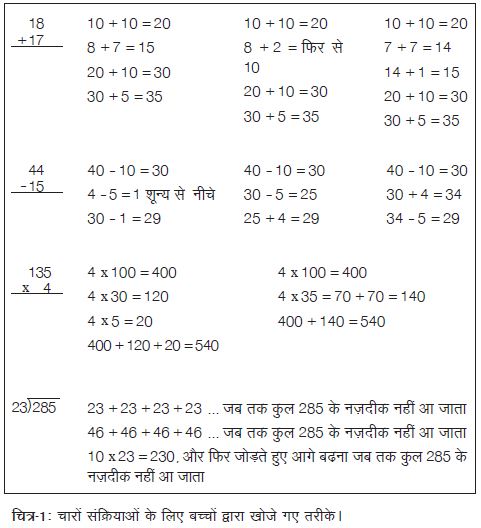 इन उदाहरणों से साफ है कि जब बच्चों को सधी-सधाई परम्परागत कलन प्रणालियों को लागू करने के लिए उकसाया जाता है तब उन्हें अपने गणितीय तरीकों व सोच को छोड़ देना पड़ता है क्योंकि बाएँ से दाएँ जाने और दाएँ से बाएँ जाने के बीच किसी भी तरह के समझौते की गुंजाइश नहीं है, इसलिए बच्चे अपने शिक्षक की बात मानते हुए अपनी सोच को एक तरफ रख देते हैं। यह वजह अपने आप में ही काफी है, यह कहने के लिए कि कलन-विधियाँ बच्चों के लिए हानिकारक हैं।
इन उदाहरणों से साफ है कि जब बच्चों को सधी-सधाई परम्परागत कलन प्रणालियों को लागू करने के लिए उकसाया जाता है तब उन्हें अपने गणितीय तरीकों व सोच को छोड़ देना पड़ता है क्योंकि बाएँ से दाएँ जाने और दाएँ से बाएँ जाने के बीच किसी भी तरह के समझौते की गुंजाइश नहीं है, इसलिए बच्चे अपने शिक्षक की बात मानते हुए अपनी सोच को एक तरफ रख देते हैं। यह वजह अपने आप में ही काफी है, यह कहने के लिए कि कलन-विधियाँ बच्चों के लिए हानिकारक हैं।
बच्चों का स्थानीय मान भूलना व संख्याओं की एक कमज़ोर समझ का बनना
जब बच्चे परम्परागत 987+ 345 = ( ) तरीकों से सरीखे सवाल हल करते हैं तब वे स्थानीय मान की अवधारणा भूल जाते हैं व उदाहरण के तौर पर सोचते व कहते हुए पाए जाते हैं, “सात व पाँच हुआ बारह। नीचे गया दो और हासिल आया एक (या दस)। एक, आठ व चार मिलकर हुए तेरह। नीचे गया तीन और हासिल आया एक (या दस)। एक, नौ व तीन मिलकर हुए तेरह।” यह विधि उन किशोरों व प्रोढ़ों के लिए सुविधाजनक है जो पहले से ही स्थानीय मान की समझ रखते हैं। प्राथमिक स्तर के छात्रों के लिए जिनकी प्रवृत्ति अमूमन ही सभी स्तम्भों को इकाई ही मान लेने की होती है, ये विधियाँ इन कमज़ोरियों को और बढ़ावा ही देती हैं।
इसके उलट यदि बच्चों को अपने खोजे तरीकों से इन सवालों को हल करने के लिए उकसाया जाए तो वे सोचते व कहते हैं, “नौ सौ और तीन सौ हुआ बारह सौ या एक हज़ार दो सौ। अस्सी व चालीस हुआ एक सौ बीस। तो यह हुआ एक हज़ार तेरह सौ बीस। इसमें जोड़ें बारह तो हो गया एक हज़ार तेरह सौ बत्तीस।” इस तरह बच्चे जिन्हें अपनी सोच विकसित करने का मौका दिया जाता है वे स्थानीय मान की अपनी अवधारणा का इस्तेमाल करते हुए उसे और भी मज़बूत व परिपक्व बना पाते हैं।
दो अलग-अलग तरीकों से हॉल-केंट स्कूल में इकट्ठी की गई जानकारी (डेटा) से इन कलन-विधियों के हानिकारक होने की बात और भी पुख्ता हो जाती है। पहला तो उन दो तरह के बच्चों से व्यक्तिगत साक्षात्कार (इंटरव्यू) जिन्हें कलन-विधियाँ सिखाई व नहीं सिखाई गईं। और दूसरा रचनावादी (constriouctivist) शिक्षकों की कक्षाओं का अवलोकन। हालाँकि हॉल-केंट स्कूल के अधिकतर शिक्षक रचनावादी सिद्धान्तों का अनुसरण करते हैं लेकिन कुछ कलन-विधियाँ भी सिखाते हैं। नीचे दी गई तालिका में कलन-विधियाँ सिखाने के आधार पर शिक्षकों का वितरण दर्शाया गया है।
बालवाड़ी: चार में से एक भी नहीं
पहली कक्षा: चार में से एक भी नहीं
दूसरी कक्षा: तीन में से एक शिक्षक
तीसरी कक्षा: तीन में से दो शिक्षक
चौथी कक्षा: सभी चारों शिक्षक
सभी कक्षाएँ विविध व तुलनीय थीं क्योंकि हर वर्ष स्कूल शु डिग्री होने से पहले प्रधानाध्यापक हर स्तर के बच्चों को क्रमरहित (randomly) तरीके से मिलाकर विभाजित कर देते थे। अन्य स्कूलों से आने वाले छात्रों को भी इसी तरह से कक्षाओं में बाँट दिया जाता था। दूसरे स्कूलों से आए ये छात्र कलन-विधियों के सहारे सही उत्तर तो निकाल लेते थे लेकिन इन्हें स्थानीय मान समझने में खासी दिक्कत आती थी।
साक्षात्कार से मिली जानकारी
मई 1990 में लिए गए व्यक्तिगत साक्षात्कारों में दूसरी कक्षा के तीन समूहों के छात्रों को हिसाब लगाने के 19 सवालों का एक पर्चा दिखलाया गया। बच्चों से कहा गया कि बिना कॉपी व पेंसिल के वे उन सवालों को हल करें व समझाएँ कि वे उत्तर तक कैसे पहुँचे। साक्षात्कारकर्ता ने उन सभी बातों को नोट किया जो बच्चों ने कहीं।
जोड़ना: साक्षात्कार में रखे गए ज़्यादातर सवालों के जवाबों में बड़ा भारी अन्तर नहीं था, खास तौर पर जब इन सवालों को परम्परागत तरीके से खड़े रूप में पूछा गया। सवालों में से एक, 7+52+186, को दो बार पूछा गया, पहली दफे खड़े स्वरूप में और दूसरी बार आड़े स्वरूप में। खड़े स्वरूप में पूछे गए सवाल पर तीन समूहों में बँटे दूसरी कक्षा के बच्चों के जवाबों में ज़्यादा अन्तर नहीं था, लेकिन सवाल के आड़े स्वरूप के उत्तरों के अन्तर चौंकाने वाले थे।
दूसरी कक्षा के इन तीन समूहों के द्वारा दिए गए जवाबों को तालिका-1 में सारगर्भित तरीके से पेश किया गया है। पहले समूह (जिसे कलन-विधि सहित समूह कहा गया है) के शिक्षक ने बच्चों को कलन-विधियाँ सिखलाई थीं जबकि बाकी दोनों समूहों के शिक्षकों ने ये विधियाँ कक्षा में नहीं सिखलाई थीं। आखिरी के दो समूह बस इस मायने में अलग थे कि तीसरे समूह (जिसे कलन-विधि रहित समूह कहा गया है) के बच्चों को अगर घर पर कुछ विधियाँ सिखाने की कोशिश की जाती तो इस समूह के शिक्षक फौरन अभिभावकों को चेतावनी भेज देते।
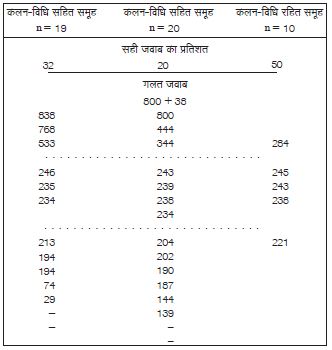
‘कलन-विधि रहित’ समूह के अधिकतर छात्र अमूमन इस तरह से अपनी व्याख्या शुरू करते, “एक सौ अस्सी और पचास हुआ दो सौ तीस।” यही कारण था कि ‘कलन-विधि सहित’ समूह के बच्चों की अपेक्षा इस समूह के चार गुना अधिक बच्चे (12% की तुलना में 45%) इस सवाल का सही जवाब दे पाए। (तालिका में डैश का चिन्ह ‘ट्ठ’ उन बच्चों को दर्शाता है जिन्होंने सवाल हल करने की कोशिश भी नहीं की और मात्र ऐसा जवाब दिया कि “मैं यह नहीं कर सकता”, “मुझे नहीं पता”, “यह सवाल करने के लिए मुझे एक पेंसिल की ज़रूरत है”, “ऐसे सवाल कक्षा में नहीं करवाए गए”, “मैं भूल गया कि शिक्षक ने क्या बतलाया था” वगैरह-वगैरह।)
 हालाँकि, महत्वपूर्ण अन्तर उन गलत जवाबों में मिले जो कि बच्चों ने सुझाए थे। तालिका-1, 2 व 3 में आड़ी लाइनों की मदद से उन जवाबों को चिन्हित किया गया है जो कि अकारण (अतर्कसंगत) ही या तो काफी बड़े या छोटे हैं। ये तमाम जवाब स्थानीय मान के अधूरे ज्ञान व संख्याओं की एक कमज़ोर समझ को उजागर करते हैं। मिसाल के तौर पर कलन-विधि समूह के दो छात्रों ने 7 + 52 + 186 का उत्तर 29 दिया। सवाल में आए तमाम अंकों को जोड़ दिया (7 + 5 + 2 + 1 + 8 + 6 = 29)। जिन छात्रों के जवाब 900 के आसपास थे उन लोगों ने संख्या 7 को 186 के 1 से जोड़ा व साथ ही दहाई के स्तम्भ से 1 हासिल लेकर आगे बढ़े। ‘कलन-विधि सहित’ समूह के छात्रों के सभी गलत जवाब या तो काफी छोटे थे या फिर काफी बड़े।
हालाँकि, महत्वपूर्ण अन्तर उन गलत जवाबों में मिले जो कि बच्चों ने सुझाए थे। तालिका-1, 2 व 3 में आड़ी लाइनों की मदद से उन जवाबों को चिन्हित किया गया है जो कि अकारण (अतर्कसंगत) ही या तो काफी बड़े या छोटे हैं। ये तमाम जवाब स्थानीय मान के अधूरे ज्ञान व संख्याओं की एक कमज़ोर समझ को उजागर करते हैं। मिसाल के तौर पर कलन-विधि समूह के दो छात्रों ने 7 + 52 + 186 का उत्तर 29 दिया। सवाल में आए तमाम अंकों को जोड़ दिया (7 + 5 + 2 + 1 + 8 + 6 = 29)। जिन छात्रों के जवाब 900 के आसपास थे उन लोगों ने संख्या 7 को 186 के 1 से जोड़ा व साथ ही दहाई के स्तम्भ से 1 हासिल लेकर आगे बढ़े। ‘कलन-विधि सहित’ समूह के छात्रों के सभी गलत जवाब या तो काफी छोटे थे या फिर काफी बड़े।
‘कुछ कलन-विधि’ समूह का प्रदर्शन बाकी दोनों समूहों के बीच में रहा। कलन-विधि समूह के 12% व कलन-विधि रहित समूह के 45% बच्चों की तुलना में इस समूह के 26% बच्चों ने सही जवाब दिया। अगर इस समूह के गलत जवाबों की रेंज को देखा जाए तो एक ओर तो न ये कलन-विधि समूह की तरह काफी फैली हुई है और न ही कलन-विधि रहित समूह के जितनी तर्कसंगत है, जिसमें मात्र दो ही जवाब, 617 व 138, सही जवाब से काफी दूर थे।
मई 1991, ठीक एक साल बाद, तकरीबन पिछले सवाल से मिलता-जुलता सवाल, 6 + 53 + 185, तीसरी व चौथी कक्षा के समूहों को हल करने के लिए दिया गया। तीसरी कक्षा के समूहों के नतीजे तालिका-2 व चौथी कक्षा के समूहों के नतीजे तालिका-3 में दर्शाए गए हैं।
एक को छोड़कर तालिका-2 व 3 के सभी स्तम्भों (columns) को कलन-विधि से लेबल किया गया है जो कि दर्शाता है कि तीसरी व चौथी के लगभग सभी बच्चों को कलन-विधियाँ सिखलाई गईं। तालिका-2 का तीसरा समूह जिसे ‘कलन-विधि रहित’ समूह से दर्शाया गया है सैली लिविंग्स्टन के द्वारा पढ़ाया गया। हालाँकि, उनके समूह में कुल 22 बच्चे थे लेकिन उनमें से केवल उन 10 को ही शामिल किया गया जिन्हें कभी भी कलन-विधियाँ नहीं सिखलाई गई थीं। बाकी 12 बच्चों को या तो कलन-विधियाँ हॉल-केंट स्कूल में ही सिखलाई गई थीं या फिर उन स्कूलों में जहाँ से वे तबादला करवा कर आए थे।
तालिका-2 में देखा जा सकता है कि ‘कलन-विधि रहित’ समूह का प्रदर्शन ‘कलन-विधि सहित’ समूह की तुलना में कहीं ज़्यादा बेहतर रहा। एक ओर जहाँ ‘कलन-विधि रहित’ समूह में से सही जवाब देने वाले छात्रों का प्रतिशत ज़्यादा था वहीं गलत मिले जवाबों की रेंज भी ‘कलन-विधि सहित’ समूह के छात्रों की तुलना में अप्रत्याशित रूप से ज़्यादा फैली हुई नहीं है। ‘कलन-विधि सहित’ समूह के छात्रों से मिले गलत जवाब पुन: स्थानीय मान के अधूरे ज्ञान व संख्याओं की एक कमज़ोर समझ की ओर इशारा करते हैं।
 तालिका-3 में दर्शाए गए चौथी कक्षा के सभी समूहों के छात्रों को पहले के सभी चारों सालों में कलन-विधियाँ सिखलाई गई थीं। इस तालिका में देखा जा सकता है कि चौथी कक्षा के छात्रों का प्रदर्शन तीसरी कक्षा के ‘कलन-विधि सहित’ समूह के छात्रों की तुलना में खराब था। हालाँकि, सही जवाब देने वाले छात्रों का प्रतिशत लगभग समान था, लेकिन चौथी कक्षा के छात्रों के गलत जवाबों के परिमाण कहीं बड़े व रोचक रूप से एक नई किस्म की गलती के साथ सामने थे: ‘8, 3, 7’ सरीखे जवाब यह दर्शा रहे थे कि इन बच्चों के दिमाग में दाएँ से बाएँ की तरफ बढ़ते हुए संख्याओं का हर स्तम्भ अलग था। न केवल इन बच्चों की स्थानीय मान की अवधारणा कमज़ोर थी बल्कि वे संख्याओं के हर स्तम्भ को बाकी स्तम्भों से अलग देख रहे थे।
तालिका-3 में दर्शाए गए चौथी कक्षा के सभी समूहों के छात्रों को पहले के सभी चारों सालों में कलन-विधियाँ सिखलाई गई थीं। इस तालिका में देखा जा सकता है कि चौथी कक्षा के छात्रों का प्रदर्शन तीसरी कक्षा के ‘कलन-विधि सहित’ समूह के छात्रों की तुलना में खराब था। हालाँकि, सही जवाब देने वाले छात्रों का प्रतिशत लगभग समान था, लेकिन चौथी कक्षा के छात्रों के गलत जवाबों के परिमाण कहीं बड़े व रोचक रूप से एक नई किस्म की गलती के साथ सामने थे: ‘8, 3, 7’ सरीखे जवाब यह दर्शा रहे थे कि इन बच्चों के दिमाग में दाएँ से बाएँ की तरफ बढ़ते हुए संख्याओं का हर स्तम्भ अलग था। न केवल इन बच्चों की स्थानीय मान की अवधारणा कमज़ोर थी बल्कि वे संख्याओं के हर स्तम्भ को बाकी स्तम्भों से अलग देख रहे थे।
 चौथी कक्षा के छात्रों से हम कम-से-कम इतनी उम्मीद तो लगाते ही हैं कि अगर उन्हें 6+53+185 का जवाब 400 से ज़्यादा या 200 से कम मिलेगा तो वे इस बात को लेकर थोड़े चिन्तित व विचलित होंगे। लेकिन चौथी कक्षा के 39% छात्र अपने द्वारा निकाले गए ऐसे जवाबों से, जिनकी रेंज एक ओर 445 से 1215 तो दूसरी ओर 134 से 194 थी, कतई विचलित नहीं दिखाई दिए। 19% प्रतिशत बच्चों ने तो तीनों संख्याओं को जोड़ने की तकलीफ तक नहीं उठाई। इस आधार पर हम यह कह सकते हैं कि चौथी कक्षा के छात्र जिन्हें पहली से लेकर चौथी तक कलन-विधियाँ सिखलाई गईं, उनका प्रदर्शन दूसरी कक्षा के उन छात्रों की तुलना में काफी खराब रहा जिन्हें ये विधियाँ नहीं सिखाई गई थीं।
चौथी कक्षा के छात्रों से हम कम-से-कम इतनी उम्मीद तो लगाते ही हैं कि अगर उन्हें 6+53+185 का जवाब 400 से ज़्यादा या 200 से कम मिलेगा तो वे इस बात को लेकर थोड़े चिन्तित व विचलित होंगे। लेकिन चौथी कक्षा के 39% छात्र अपने द्वारा निकाले गए ऐसे जवाबों से, जिनकी रेंज एक ओर 445 से 1215 तो दूसरी ओर 134 से 194 थी, कतई विचलित नहीं दिखाई दिए। 19% प्रतिशत बच्चों ने तो तीनों संख्याओं को जोड़ने की तकलीफ तक नहीं उठाई। इस आधार पर हम यह कह सकते हैं कि चौथी कक्षा के छात्र जिन्हें पहली से लेकर चौथी तक कलन-विधियाँ सिखलाई गईं, उनका प्रदर्शन दूसरी कक्षा के उन छात्रों की तुलना में काफी खराब रहा जिन्हें ये विधियाँ नहीं सिखाई गई थीं।
घटाना: जिस जोड़ने के सवाल पर अभी तक चर्चा की गई है उसे आड़े स्वरूप में छात्रों के सामने रखा गया था, जिस वजह से ये प्रश्न उन छात्रों के लिए कठिन था जो कलन-विधियों के आदी हैं। संख्याओं को घटाने का एक अन्य सवाल जो मई 1991 में छात्रों से अपने खड़े स्वरूप में पूछा गया था, नीचे दिया गया है;
504
–306
दूसरी व तीसरी कक्षा के उन छात्रों ने जिन्होंने ऐसे सवालों को हल करने के अपने तरीके निकाले थे, ने कहा, “500 से 300 गया, हुआ 200। 4 में से 6 गया, बचा शून्य से 2 कम; तो जवाब हुआ 198।” इस तरह ‘कलन-विधि रहित’ समूह के दूसरी कक्षा के 74% छात्रों (n=19) व तीसरी कक्षा के 80% छात्रों (n=10) ने सवाल का सही जवाब दिया। इन समूहों से मिले गलत जवाब भी 200 से ज़्यादा दूर नहीं थे; दूसरी व तीसरी कक्षा से मिले गलत जवाब क्रमश: 320, 202, 202, 200 व 194 और 202 व 190 थे।
‘कलन-विधि सहित’ समूह के जिन छात्रों ने सवाल के सही जवाब दिए तीसरी कक्षा में उनका प्रतिशत मात्र 42% व 35% था और वहीं चौथी कक्षा में 55%, 39%, 38% व 29% था। ये सभी प्रतिशत ‘कलन-विधि रहित’ समूह के दूसरी व तीसरी कक्षाओं की तुलना में काफी कम थे। तीसरी व चौथी कक्षा के ‘कलन-विधि सहित’ समूह के छात्रों से मिले गलत जवाबों को तालिका-4 में सारगर्भित रूप में पेश किया गया है। तालिका के आँकड़े पुन: दर्शाते हैं कि गलत जवाब ‘कलन-विधि रहित’ समूहों की तुलना में कहीं विशाल व उनकी रेंज ज़्यादा फैली हुई थी।
 जैसा कि पहले कहा गया है कि सवालों के खड़े स्वरूप को हल करना कलन-विधि सीखे हुए छात्रों के लिए कहीं ज़्यादा आसान होता है, लेकिन इस घटाने के सवाल में प्रश्न का यह स्वरूप भी ‘कलन-विधि सहित’ समूह के छात्रों की मदद नहीं कर पाया। क्योंकि इन बच्चों की स्थानीय मान की अवधारणा कमज़ोर थी इसीलिए उन्होंने संख्या 504 के 5 (जिसका स्थानीय मान 100 है) में से 10 उधार लेकर व 4 में से 3 को घटाकर उत्तर में 108 की संख्या निकाली। वे जिन्हें उत्तर में 208 की संख्या मिली उन्होंने 10 को बिना कहीं से उधार लिए 4 में जोड़ा! तालिका-4 में मिले 8 से अन्त होने वाले गलत उत्तर चौंकाने वाले हैं; ये उत्तर दर्शाते हैं कि छात्रों ने 14 में से 6 को घटाना तो सीख लिया है लेकिन उन्हें यह नहीं पता कि 10 आया कहाँ से।
जैसा कि पहले कहा गया है कि सवालों के खड़े स्वरूप को हल करना कलन-विधि सीखे हुए छात्रों के लिए कहीं ज़्यादा आसान होता है, लेकिन इस घटाने के सवाल में प्रश्न का यह स्वरूप भी ‘कलन-विधि सहित’ समूह के छात्रों की मदद नहीं कर पाया। क्योंकि इन बच्चों की स्थानीय मान की अवधारणा कमज़ोर थी इसीलिए उन्होंने संख्या 504 के 5 (जिसका स्थानीय मान 100 है) में से 10 उधार लेकर व 4 में से 3 को घटाकर उत्तर में 108 की संख्या निकाली। वे जिन्हें उत्तर में 208 की संख्या मिली उन्होंने 10 को बिना कहीं से उधार लिए 4 में जोड़ा! तालिका-4 में मिले 8 से अन्त होने वाले गलत उत्तर चौंकाने वाले हैं; ये उत्तर दर्शाते हैं कि छात्रों ने 14 में से 6 को घटाना तो सीख लिया है लेकिन उन्हें यह नहीं पता कि 10 आया कहाँ से।
कलन-विधियाँ सीखे हुए छात्रों की संख्याओं के बारे में कमज़ोर समझ न केवल इस बात का परिणाम है कि उन्हें स्थानीय मान की अवधारणा का अपर्याप्त ज्ञान है बल्कि इस वजह से भी कि संख्याओं के स्तम्भों के बीच कोई रिश्ता न देखते हुए उनके बारे में अलग-अलग सोचना उनकी आदत बन गई है। यह आदत खास तौर पर उन बच्चों के लिए और भी उभरकर सामने आती है जिन्होंने तालिका-4 में दर्शाए अनुसार दाएँ से बाएँ बढ़ते हुए ‘8, 0, 1’ सरीखे जवाब दिए। अगर इन बच्चों ने संख्याओं को समग्र रूप में देखते हुए लगभग 300 को लगभग 500 से घटाया होता तो उन्हें मालूम होता कि जवाब लगभग 200 ही होगा।
जब दूसरी व तीसरी कक्षा के छात्र चौथी कक्षा के छात्रों की तुलना में कहीं ज़्यादा बेहतर प्रदर्शन कर रहे हों तब हम इसी निष्कर्ष पर पहुँचते हैं कि शुरुआती कक्षाओं में कलन-विधियों का इस्तेमाल एक काफी बड़ी गलती है।
कक्षा अवलोकन से मिली जानकारी
रचनावादी शिक्षकों की कक्षाओं में आने से पहले कलन-विधि सीखे छात्रों के प्रदर्शन के नतीजों ने हमें कलन-विधियों के हानिकारक प्रभावों के बारे में आश्वस्त कर दिया था। ये छात्र आसानी-से विधियों की मदद से सही जवाब तो देते लेकिन स्थानीय मान की अवधारणा में उन्हें काफी दिक्कत थी। जब तक वे अपने तरीके को समझा पाए, हमने उन्हें उनके मनचाहे तरीके को अपनाकर उत्तर देने दिया।
अपने तरीके को समझाने के दबाव के चलते, तबादला लेकर आए औसत से ऊपर दर्जे के छात्रों ने फौरन ही ये स्वीकार कर लिया कि सवाल हल करने का बाएँ से दाएँ की ओर चलने वाला उनके सहपाठियों का तरीका आसान है। इसके उलट, औसत दर्जे के छात्र कलन-विधियों का इस्तेमाल करते रहे व अन्तत: स्थानीय मान को समझ पाए। औसत से कम दर्जे के छात्र स्थानीय मान की अपनी कमज़ोर समझ में बिना किसी बढ़ोतरी के कलन-विधियों का इस्तेमाल करते रहे। कलन-विधियों का इस्तेमाल सही नतीजों तक पहुँचने की दिशा में एक तरह की सुरक्षा प्रदान करता है, ऐसे में औसत से कम दर्जे के छात्र ऐसी मशीनों की तरह काम करते रहे जिनके प्रोग्रामों को हटाया नहीं जा सकता। या यूँ कहें कि ऐसी मशीनों की तरह जिनकी कार्यप्रणाली बदली नहीं जा सकती। उनकी सोच इस प्रोग्राम की वजह से बाधित व पंगु बनी रही।
कलन-विधियों के हानिकारक प्रभाव और भी उभरकर सामने आए जब 1991-92 में चौथी कक्षा की एक शिक्षिका, चेरिल इनग्राम, ने रचनावादी तरीका अपनाने का निर्णय लिया। चौथी कक्षा को 10 वर्षों तक पढ़ाने के बाद चेरिल ने ऐसा फैसला इसलिए लिया क्योंकि उन्होंने पाया कि जो बच्चे पहले, दूसरे व तीसरे वर्षों में रचनावादी कक्षाओं में पढ़े हैं वे गणित के बेहतर छात्र हैं। एक रचनावादी शिक्षक की दिशा में आगे बढ़ने में उनकी मदद करने के उद्देश्य से गणित के पीरियड में मैं उनकी कक्षा में लगभग पूरे साल बैठी। मैं यह देखकर दंग थी कि चौथी कक्षा के बच्चों के दिमागों से कलन-विधियों को निकाल पाना कितना मुश्किल काम है। आगे दिया गया विवरण दिखलाता है कि किस हद तक बच्चों की समझ स्थानीय मान व संख्याओं के स्तम्भों को अलग-अलग देखने को लेकर कमज़ोर है।
चेरिल जिस तरीके को अपनाकर बच्चों की सोच को कलन-विधियों से दूर ले जाना चाह रही थीं, वह था ब्लैकबोर्ड पर सवालों को आड़े स्वरूप में उनके सामने रखना, जैसे कि 876+359, व उनसे कहना कि बिना पेंसिल का इस्तेमाल किए वे इस प्रश्न का उत्तर निकालने के तरीके सुझाएँ। आगे बढ़कर जब बच्चे ये समझाने की कोशिश करते कि उन्हें अपने दिमाग में कलन-विधि का प्रयोग करते हुए 1235 उत्तर कैसे मिला, तब चेरिल उनकी बातों का अनुपालन करते हुए हर एक स्तम्भ के लिए कुछ इस तरह से बोर्ड पर लिखतीं:
15
13
+12
जब बच्चा यह समझा चुका होता कि उसे 1235 उत्तर कैसे मिला तब चेरिल कहतीं, “लेकिन मुझे तो तुम्हारे तरीके का पालन करते हुए उत्तर में 40 मिला। तुम्हें कैसे 1235 मिला?” ज़्यादातर बच्चे चेरिल के इस सवाल को सुन चकराकर चुप हो गए। लेकिन फिर एक बच्चे ने ध्यान दिलाया कि शिक्षक ने बोर्ड पर जो 13 लिखा है वो असल में 130 व 12 असल में 1200 के लिए है।
इस तरह की स्थानीय मान से जुड़ी कमियों को दूर करना अपेक्षाकृत आसान था। जो मुश्किल लगातार बनी रही, वह थी संख्याओं को समग्र रूप में न देखकर अलग-अलग स्तम्भों के रूप में देखने की। ऊपर पूछे गए सवाल के जवाब स्वरूप बच्चे स्तम्भों के मुताबिक टुकड़ों में जवाब देते रहे, जैसे कि “15 (6+9 के लिए), 130 (10+70+50 के लिए), व 1200 (100+800+300 के लिए)।”
बच्चों को समग्र संख्याओं के बारे में सोचने की दिशा देने के प्रयास में हम लोगों ने 28 अक्टूबर 1991 को एक प्रयोग किया। चेरिल ने एक के बाद एक ऐसे सवालों को बोर्ड पर लिखा जिसमें किसी एक संख्या में 99 शामिल हो, उदाहरण के तौर पर 366 + 199, 493 + 99, और 601 + 199। क्लास में पूरे घण्टे भर चेरिल ऐसे ही सवालों को कक्षा के सामने कई तरीकों से हल करने के लिए रखती रहीं।
लगभग सभी बच्चे कलन-विधि का अनुपालन करते हुए उस पूरे एक घण्टे के दौरान संख्याओं को जोड़ते रहे। पहले इकाई के अंकों को, फिर 10 को हासिल लेते हुए दहाई के अंकों को और फिर 100 को हासिल लेते हुए सैकड़े के अंकों को। लेकिन इनमें से एक बच्चे ने, जिसे हम ‘जो’ नाम दे देते हैं और जो कि पहली कक्षा से ही रचनावादी क्लास में पढ़ा था, कुछ इस तरह से सवालों का जवाब दिया: “मैंने 366+199 को 200+365 में बदल लिया, और मेरा जवाब है 565।” घण्टा-भर चली इस तरह की ‘अन्त:-क्रिया (interaction)’ के बाद मात्र तीन अन्य बच्चे ही ‘जो’ के तरीके की नकल कर रहे थे! बाकी सभी बच्चे कलन-विधि का पालन करते हुए संख्याओं के अलग-अलग स्तम्भों को हल करने में मशगूल थे।
इस दौरान, अक्टूबर महीने के बीच में, चेरिल ने एक टिपण्णी की कि उसके पिछले 10 सालों के चौथी कक्षा को पढ़ाने के अनुभव में उसने कभी भी गणित को लेकर इतना उत्साह और जिज्ञासा नहीं देखी थी। नवम्बर महीने की शुरुआत में उसने कक्षा में यह घोषणा कर दी कि हम लोगों को जोड़ने और घटाने के ऐसे तरीके खोजने होंगे जिनमें हासिल और उधार लेने की ज़रूरत ही न पड़े। इस ज़रूरत ने कक्षा के माहौल में एक रचनात्मकता का संचार किया और एक लड़की, जो पहले काफी निष्क्रिय-सी रहती थी, अपने हाथ आत्मविश्वास से हिलाने लगी। 19 नवम्बर को उसने एक सवाल को हल करने के लिए एक ऐसा तरीका खोज निकाला जो संख्याओं को समग्र रूप से देखने की उसकी सोच की ओर इशारा करता है।
600 – 100 + 500
6 – 49 = नेगेटिव 43
500 – 43 = 457
कक्षा में कई मौके ऐसे आए जिसने हौसला बढ़ाया तो कई बार निराशा भी हाथ लगी। 20 दिसम्बर का दिन ऐसे ही निराश करने वाला एक दिन था। चेरिल ने कक्षा में कहा कि उसके पास क्रिसमस के मौके पर तोहफों पर खर्च करने के लिए 50 डॉलर हैं। वो यह जानना चाहती थी कि क्या उसके पास इतने पैसे हैं कि वो नीचे दिए तमाम उपहार खरीद सके:
3 बैटलशिप (एक खेल) @ 7.99
2 स्वेटर @ 11.99
1 पर्स 15.00
2 गुड़िया @ 8.95
पहला बच्चा जो जवाब देने के लिए आगे आया उसने शुरू किया, “नौ धन नौ धन पाँच बराबर 23।”
21 जनवरी वो पहला दिन था जब कलन-विधि इस्तेमाल करने वाले छात्रों की तरफ से बाएँ से दाएँ की ओर चलने वाला तरीका सामने आया। चेरिल ने नीचे दिए गए दामों को बोर्ड पर लिखकर कुल खर्च का हिसाब मांगा:
शर्ट Š 5.00
टी-शर्ट Š 1.95
स्वेटर Š 37.90
हमेशा की तरह एक छात्र ने पूछा, “क्या मैं दाईं ओर से शुरू कर सकता हूँ?” एंड्रू ने तुरन्त ही टोकते हुए कहा, “बाईं ओर से शुरू करना ज़्यादा आसान होगा।” रॉब ने भी एंड्रू की हाँ-में-हाँ मिलाई। एंड्रू ने समझाते हुए कहा कि 37+1+5 हुए 43 डॉलर और 90 सेंट्स अ 10 सेंट्स हुए एक डॉलर, इस तरह कुल खर्च होगा 44 डॉलर व 85 सेंट्स।
हालाँकि, जनवरी 25 का दिन एक और निराशा का दिन था। चेरिल ने बोर्ड पर योग का एक सवाल कुछ इस तरह से हल करने के लिए दिया जिसमें संख्याएँ एक-दूसरे के नीचे ठीक से जमाई नहीं थीं और एंड्रू ने 160 का उत्तर देते हुए समझाते हुए कहा:
25
3
4
+ 65
20 + 30 = 50
40 + 60 = 100
150 + 10 = 160
जब चेरिल ने सवाल किया कि और कौन एंड्रू से सहमत है तो पाँच अन्य छात्रों ने अपने हाथ उठाए।
लेकिन फिर भी साल के अन्त तक बच्चों ने काफी प्रगति कर ली थी और मई 1992 में लिए गए साक्षात्कारों के नतीजे 1991 की तुलना में कहीं बेहतर थे। सवाल 6+53+185 का सही हल देने वाले छात्रों का प्रतिशत 1991 के 17% (देखें तालिका-3) से बढ़कर 1992 में 75 प्रतिशत हो गया। गलत जवाबों की रेंज भी काफी कम होकर 28, 202, 234, 238, और 243 रह गई। चित्र-2 कलन-विधि के इस्तेमाल व सही जवाबों की आवृति के बीच के सम्बन्ध को दर्शा रहा है। यहाँ देखा जा सकता है कि 1991 में चेरिल की कक्षा के सत्रह में से तेरह (76%) बच्चों ने कलन-विधियों का इस्तेमाल करते हुए गलत हल निकाले। वहीं इसके उलट 1992 में बीस में से पन्द्रह (75%) बच्चे अपने खोजे तरीकों से सही जवाब निकाल पाए। यह विश्लेषण सुझाता है कि बच्चों द्वारा अपनी सोच का इस्तेमाल कर सही उत्तर निकालने की गुंजाइश ज़्यादा है।
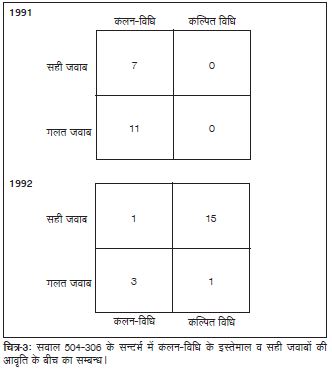
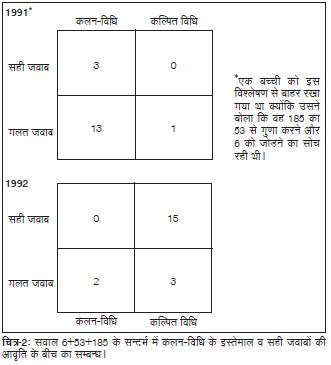 जहाँ तक घटाने के प्रश्न (खड़े स्वरूप में 504–306) का मामला है, सही जवाब देने वालों का प्रतिशत 39% (1991 में) से बढ़कर 80% (1992 में) हो गया। 1992 में जो गलत जवाब मिले, वे थे: 90, 108, 200, और 202। ये गलत हल भी पहले (देखें तालिका-4) की तुलना में कहीं तर्कसंगत थे। जैसा कि चित्र-3 में देखा जा सकता है, सभी बच्चे 1991 में परम्परागत विधियों का इस्तेमाल करते थे, और 18 में से 7 (39%) बच्चों ने ही सही जवाब दिया। इसके उलट, 1992 में बीस में से सोलह बच्चों ने अपने खोजे तरीकों का इस्तेमाल किया और पन्द्रह (75%) बच्चों ने सही जवाब दिया। यह विश्लेषण पुन: यह सुझाता है कि जो बच्चे सवालों को हल करने के लिए अपनी सोच का इस्तेमाल करते हैं उनकी सही उत्तर निकालने की गुंजाइश ज़्यादा है।
जहाँ तक घटाने के प्रश्न (खड़े स्वरूप में 504–306) का मामला है, सही जवाब देने वालों का प्रतिशत 39% (1991 में) से बढ़कर 80% (1992 में) हो गया। 1992 में जो गलत जवाब मिले, वे थे: 90, 108, 200, और 202। ये गलत हल भी पहले (देखें तालिका-4) की तुलना में कहीं तर्कसंगत थे। जैसा कि चित्र-3 में देखा जा सकता है, सभी बच्चे 1991 में परम्परागत विधियों का इस्तेमाल करते थे, और 18 में से 7 (39%) बच्चों ने ही सही जवाब दिया। इसके उलट, 1992 में बीस में से सोलह बच्चों ने अपने खोजे तरीकों का इस्तेमाल किया और पन्द्रह (75%) बच्चों ने सही जवाब दिया। यह विश्लेषण पुन: यह सुझाता है कि जो बच्चे सवालों को हल करने के लिए अपनी सोच का इस्तेमाल करते हैं उनकी सही उत्तर निकालने की गुंजाइश ज़्यादा है।
गुणा करने के प्रश्न (13 x 11) का सही जवाब देने वालों का प्रतिशत 1991 में 6% से बढ़कर 1992 में 55% तक पहुँच गया। इन दो वर्षों में दिए गए गलत उत्तर थे:
1991: 11, 13, 42, 64, 113, 133, 133, 141, 144 (आठ बच्चों ने हल निकालने की कोशिश नहीं की)
1992: 113, 133, 144, 233, 300
 हालाँकि, 1992 में की गई पड़ताल व जानकारी के नतीजे बेहतर थे लेकिन चौथी कक्षा के इन छात्रों के लिए यह नहीं कहा जा सकता कि ये कलन-विधियों के हानिकारक प्रभावों से पूरी तरह उबर चुके थे। कक्षा में कई बच्चे जोड़ने-घटाने के सवालों को हल करने के लिए संख्याओं के हर स्तम्भ को अलग-अलग देखने का मशीनी तरीका इस्तेमाल करते रहे। संज्ञानात्मक तौर पर आगे बढ़े हुए बच्चे साल के अन्त तक कलन-विधियों के प्रभावों से मुक्त होने के करीब पहुँच पाए। औसत से कमतर बच्चे कलन-विधियों से चिपके रहे और उनकी स्थानीय मान की समझ कमज़ोर बनी रही। कम्प्यूटर के बनिस्बत इन्सानों को अन-प्रोग्राम करना ज़्यादा मुश्किल काम है, और कक्षा में पीछे रहने वाले बच्चों पर कलन-विधियों का सबसे ज़्यादा प्रभाव था।
हालाँकि, 1992 में की गई पड़ताल व जानकारी के नतीजे बेहतर थे लेकिन चौथी कक्षा के इन छात्रों के लिए यह नहीं कहा जा सकता कि ये कलन-विधियों के हानिकारक प्रभावों से पूरी तरह उबर चुके थे। कक्षा में कई बच्चे जोड़ने-घटाने के सवालों को हल करने के लिए संख्याओं के हर स्तम्भ को अलग-अलग देखने का मशीनी तरीका इस्तेमाल करते रहे। संज्ञानात्मक तौर पर आगे बढ़े हुए बच्चे साल के अन्त तक कलन-विधियों के प्रभावों से मुक्त होने के करीब पहुँच पाए। औसत से कमतर बच्चे कलन-विधियों से चिपके रहे और उनकी स्थानीय मान की समझ कमज़ोर बनी रही। कम्प्यूटर के बनिस्बत इन्सानों को अन-प्रोग्राम करना ज़्यादा मुश्किल काम है, और कक्षा में पीछे रहने वाले बच्चों पर कलन-विधियों का सबसे ज़्यादा प्रभाव था।
बच्चों का सवालों को लिखने की व्यवस्था व अन्य लोगों पर निर्भर हो जाना
साक्षात्कारों के दौरान ‘कलन-विधि रहित’ व ‘कलन-विधि सहित’ समूहों के छात्रों ने सवालों को हल न करने के कारण अलग-अलग बतलाए। ‘कलन-विधि सहित’ समूह के बच्चों ने कुछ ऐसे कारण दिए: “मुझे पेंसिल की ज़रूरत होगी”, “ऐसे सवाल कक्षा में करवाए नहीं गए” या फिर “मैं भूल गई कि शिक्षक ने क्या बतलाया था”। जहाँ ये छात्र पेंसिल-पेपर, सवालों को लिखने की व्यवस्था (खड़े या आड़े), व अन्य लोगों पर निर्भरता जता रहे थे वहीं ‘कलन-विधि रहित’ समूह के बच्चों का कहना था, “मैं यह नहीं कर सकती”, “मुझे नहीं पता कैसे” या फिर कुछ ऐसा ही जिसमें उनकी अपनी कमी झलकती हो।
निश्चित तौर पर रचनावादी कक्षा के छात्र कुछ सवालों का हल नहीं निकाल पाए। लेकिन इन बच्चों ने पेंसिल-पेपर, सवालों को दर्शाने के तरीके (खड़े या आड़े), व अन्य लोगों पर निर्भर होना नहीं सीखा है। कलन-विधियाँ बच्चों को सवालों का सही हल निकालने के लिए समर्थ तो बनाती हैं लेकिन उसका अतिरिक्त प्रभाव (साईड इफेक्ट) है आत्म-निर्भरता का खो जाना।
अन्त में
कलन-विधियाँ व ‘वैकल्पिक’ या ‘अनौपचारिक’ तरीकों पर पिछले कई वर्षों से कई तरह से विचार किया गया है। कुछ लोग कलन-विधियों की वकालत करते हैं व अनौपचारिक तरीके सिखाने पर ज़ोर देते हैं1। ब्राज़ील2 व इंग्लैंड3 के कुछ अन्य लोगों ने कलन-विधियाँ सीखने के आग्रह पर सवाल उठाए हैं। एक तीसरे समूह ने, कई नज़रियों से आग्रह किया है कि हम कलन-विधियाँ सिखाना बन्द करें। यह रवैया न केवल सयुंक्त राज्य अमरीका4 बल्कि डेनमार्क5, इंग्लैंड6, हॉलैंड7 और दक्षिणी अफ्रीका8 से भी उभरकर सामने आया है। हम तीसरे समूह का समर्थन करते हुए एक कदम और आगे जाकर यह कहते हैं कि प्राइमरी कक्षाओं के छात्रों के लिए कलन-विधियों का इस्तेमाल हानिकारक है।
कॉन्सटेंस कामी: अलाबामा विश्वविद्यालय, बरमिंगघम के डिपार्टमेंट ऑफ करीकुलम एंड इंस्ट्रक्शन में अर्ली चाइल्डहुड एजुकेशन प्रोग्राम की प्रोफेसर।
अँग्रेज़ी से अनुवाद: विवेक मेहता: आई.आई.टी., कानपुर से मेकेनिकल इंजीनियरिंग में पीएच.डी. की है एवं तेज़पुर विश्वविद्यालय, असम में पढ़ा रहे हैं।



