जादुई तालाब की पहेली

विजय शंकर वर्मा

हजामत बनाते हुए पुश्तैनी नाई ने एक साधारण-सी पहेली पूछी थी। परन्तु, देखिए क्या क्या समझ सकते हैं एक अदनी-सी पहेली के जरिए, अगर उसकी गहराइयों में जाने की कोशिश करें।

छुट्टियों के दौरान मैं अपने घर पटना गया हुआ था। एक सुबह हमारा पुश्तैनी नाई गांव से आ पहुंचा। फिर क्या था ० परिवार के सारे पुरुषों को बाल कटवाने के लिए लाइन लगानी पड़ी। पिछली बार जब मैं उससे मिला था मैं स्नातक की कक्षाओं में पढ़ रहा था; यह बात करीब बीस साल पहले की होगी। यानी जब वो बाल काट रहा था तो हमारे पास बहुत कुछ था बतियाने को। वो जानना चाहता था कि मैं क्या करता हूं अपनी जीविका चलाने के लिए।

उसे यह जानकर काफी अच्छा लगा कि मैं दिल्ली विश्वविद्यालय में पढ़ा रहा हूं; पर वो जानना चाहता था कि मैं क्या पढ़ाता हूं वहां। जब मुझे यह समझाना मुश्किल लगा कि भौतिक शास्त्र क्या है, तो मैंने उससे कहा कि मैं ‘हिसाब' पढ़ाता हूं यानी कि ऐसा कुछ जिसमें गणनाएं होती हैं। यह सुनकर वह खुश हो गया और शरारत भरी मुस्कुराहट के साथ उसने कहा, “ऐसा है, तो फिर तुम इसका हल ढूंढ ही लोगे।'' और उसने ये पहेली मेरे सामने पेश कर दी।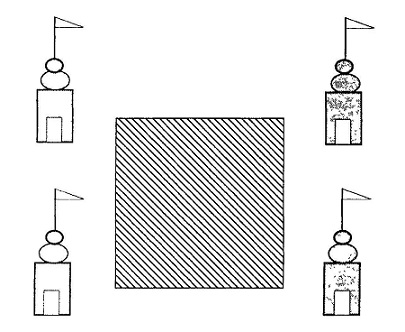

"गांव के बाहर एक तालाब है जिसका पानी जादुई है। यह तालाब वर्गाकार है और उसके हर कोने पर अलग-अलग देवताओं के मंदिर बने हुए हैं। जादुई पानी की वजह से, पानी से धोने पर फूलों की संख्या दुगनी हो जाती है और पूजारी उसमें से कुछ फूल पहले देवता को चढ़ा देता है। शेष फूलों को, क्योंकि वो बचे हुए हैं। -- एक तरह से जूठे हैं, इसलिए उन्हें फिर से तालाब में धोता है। उनकी संख्या फिर से दुगनी हो जाती है। फिर वो दूसरे देवता को उतने ही फूल चढ़ाता है जितने उसने पहले देवता को चढ़ाए थे --- ताकि उन्हें बुरा न लग जाए क्योंकि सब देवता एक-दूसरे से अत्यंत ईर्ष्या करते हैं। बचे हुए फूल फिर से धोता है, और वे फिर दुगने हो जाते हैं। तीसरे देवता के साथ भी वो वही करता है जैसा पहले दो के साथ किया था और फिर चौथे देवता के साथ। अंत में बिल्कुल भी फूल नहीं बचते। मेरे दोस्त, पुजारी ने कितने फूल तोड़े और कितने कितने हर देवता को चढ़ाए।''
जब वो हजामत कर रहा था तो मैंने हल सोचने की कोशिश की पर असफल रहा। फिर जब मैंने परेशान होते हुए कागज़ और पेंसिल निकालकर जवाब ढूंढने की कोशिश की तो वो मुस्कुरा रहा था। पहेली बहुत मुश्किल नहीं थी और जब मैंने उसे जवाब बताया तो वो ज़ोर से हंस दिया। वो खुश था कि उसने मुझे ऐसी पहेली बुझाई कि मुझे भी मेहनत करनी पड़ी, और साथ ही इसलिए भी खुश था कि उसके गांव का यह लड़का, जो अब ‘यूनिवर्सिटी में मास्टर बन गया था, उसकी परीक्षा में खरा उतरा था।

मेरा सुझाव है कि इस लेख को यहीं छोड़कर, और आगे पढ़ने से पहले, आप भी इस पहेली को हल करने की कोशिश करें। मेरा वायदा है कि आपके लिए भी ये अनुभव काफी मजेदार रहेगा।

पारंपरिक गणितीय तरीका
इस पहेली को हल करने के बहुत से तरीके हैं और मैं शुरुआत में उनमें से जवाब देने का सबसे ज्यादा घिसा-पिटा तरीका बताऊंगा - जिस तरीके से मैंने उस दिन इसे हल किया था। इसमें सबसे पहले उचित समीकरण लिख लिया जाता है और फिर उसका हल ढूंढा जाता है। हम मान लेते हैं कि 'x' वह संख्या है जितने पुजारी ने तोड़े थे और 'y' फूल उसने हर देवता को चढ़ाए। चूंकि हर बार धोने पर फूलों की संख्या दुगनी हो जाती है, पहली बार देवता को चढ़ावा देने के पश्चात (2x-y) फूल बचेंगे। फिर से पानी में डुबाने पर फूल दुगने हो जाते हैं इसलिए दूसरे चढ़ावे के बाद 2(2x-y)-y फूल शेष रहेंगे। ऐसा ही दो बार और होता है और अंत में एक भी फूल नहीं बचता, इसलिए अंतिम समीकरण इस तरह होगीः

2(2(2(2x-y)-y)-y)-y = 0
हमें इस समीकरण का हल ढूंढना है। इसे सरल रूप देने पर:
16x-8y-4y-2y-y = 0
अथवा 16 x -(1+2+4+8) y = 0
यानी कि 16x-15y = 0
चूंकि एक ही समीकरण से हमें दो अनजानी मात्राओं का पता लगाना है इसलिए इस समीकरण का केवल एक हल नहीं हो सकता साथ ही हमें यह भी ध्यान रखना होगा कि इसका पूर्णांक हल ही संभव है क्योंकि पहेली फूलों की संख्या पर आधारित है जो अपूर्णांक नहीं हो सकती।
इसलिए इस समीकरण का सामान्य हल इस प्रकार लिखा जा सकता है:
X = 15j,   y = 16j ; जहां    j = 1, 2, 3, . . .

इसलिए सबसे पहला संभव जवाब x = 15, y = 16 होगा; यानी कि पूजारी ने 15 फूल तोड़े और हर देवता को 16 फूल चढ़ाए।

कुछ साल पहले के इस अनुभव के बाद मैंने ये पहेली बहुत से लोगों से पूछी है; उनमें से कुछ-एक ने तो जवाब ढूंढने में घंटों लगा दिए, जबकि कई लोग ऐसे भी थे जिन्होंने पहेली सुनते ही हल बता दिया। इससे स्पष्ट है कि अलग-अलग लोग जवाब ढूंढने के लिए अलग-अलग तरीके अपनाते हैं। यहां मैं आपको इस पहेली को हल करने के कुछ ऐसे तरीके दिखा रहा हूं जिनमें बीजगणित के इस्तेमाल की ज़रूरत नहीं है।

समझ-बूझकर तुक्का लगाना
किसी भी सवाल को हल करने के लिए तुक्का तो लगाया ही जा सकता है। परन्तु ऐसे ही अंधेरे में तीर चला देना अक्सर ज्यादा सार्थक नहीं होता है। और मान लीजिए अगर अंदाज़ लगाना ही है। तो पहेली के महत्वपूर्ण पहलुओं के बारे में सोचते हुए कुछ कहना कहीं बेहतर होता है।

1. इस सवाल में सबसे पहली गौर करने लायक बात यह है कि पूजारी जितने फूल का चढ़ावा देता है वह संख्या सम होगी। ऐसा इसलिए जरूरी है क्योंकि हर बार देवता को चढ़ाने से पहले फूल पानी में डुबोए जाते हैं, हर बार बराबर संख्या में फूल चढ़ाए जाते हैं और अंतिम बार फूल चढ़ाने के बाद कुछ भी शेष नहीं रहता। इसका अर्थ यह हुआ कि 'y' राशि सम संख्या होगी।

2. पुजारी ने जितने फूल तोड़े उनकी संख्या 'x', जितने फूल उसने चढ़ाए उससे कम हो यह जरूरी है, नहीं तो हर बार चढ़ावे के बाद फूलों की संख्या बढ़ती ही जाएगी। यानी कि अगर ऐसा नहीं हुआ तो पहले देवता के चढ़ावे के बाद बचे फूलों की संख्या (2x-y) शुरुआत में तोड़े फूलों की संख्या 'x' से ज्यादा हो जाएगी।

3. पहली बार तोड़े फूलों की संख्या (x), जितने फूल चढ़ाए जाते हैं। उससे आधी या आधे से ज्यादा होना जरूरी है नहीं तो पहली बार चढ़ाने के लिए भी पर्याप्त फूल नहीं होंगे।

4. अंत में, हमें छोटी संख्याओं से शुरू करना होगा ताकि छोटे से छोटे पूर्णांक हल ढूंढे जा सकें।

इन सीमाओं को ध्यान में रखते हुए हमें इस संभावना से शुरुआत कर सकते हैं: x = 1, y = 2. हालांकि तुरन्त समझ में आ जाता है कि यह सही हल नहीं है, फिर भी इन संख्याओं को देखकर एक बात तो दिमाग में जरूर कौंधती है कि अगर चढ़ावा देने के लिए चार के बजाए एक ही देवता होता तो हल यही था।

चूंकि ज़रूरी है कि 'y' सम संख्या हो इसलिए अगला संभव जवाब y = 4 एवं x = 2 अथवा 3 हो सकता है। x = 2 और y = 4 तो पिछले हल का दुगना भर है, इसलिए उसे नज़रअंदाज किया जा सकता है। x = 3, y = 4 भी हमारी पहेली का हल नहीं है, परन्तु यहां भी स्पष्ट है कि अगर दो ही देवता होते तो यह हल एकदम फिट बैठ जाता।

इतना सोच लेने के बाद एक पैटर्न उभरता दिखता है -जैसे जैसे देवताओं की संख्या बढ़ती जाती है, 'y' दुगना हो रहा है और 'x' का मान उससे एक कम है। इसका अर्थ निकलता है कि अगर तीन देवता हों तो पहेली का हल होना चाहिए : y = 8, x = 7 तीन देवताओं पर आजमाने पर यह जवाब सही निकलता है। अब तो पक्का है कि क्योंकि हमारे सवाल में चार देवता हैं इसलिए हल यही होगाः
y = 16, x = 15

सिद्धांत का सामान्यीकरण
इस तरह सोच-समझकर अंदाज़ लगाते हुए हमने न केवल पहेली का सही हल बूझ लिया, बल्कि हम एक सामान्य सिद्धांत की तरफ बढ़ सकते हैं कि अगर तालाब की भुजाओं की संख्या 'N' हो जिसके किनारों पर उतने ही देवताओं के मंदिर बने हुए हों तो पहेली का हल कुछ इस प्रकार होगाः  
y = 2^N एवं x = 2^N-1

इसी तरीके का इस्तेमाल करते हुए हम सामान्यीकरण की प्रक्रिया को और भी आगे बढ़ा सकते हैं कि अगर तालाब के पानी में धोने से फूलों की संख्या दुगनी होने के बजाए ‘n' गुनी हो जाए तो हेल क्या होगा?
इसका जवाब ढूंढने के लिए हमें शुरुआती समीकरण को देखना होगा जिसमें N = 4 था और n = 2 यानी कि देवता चार थे और पानी से धोने पर फूल दुगने हो जाते थे। उस समय हमने यह समीकरण लिखी थी।
16 x - (1+2+4+8) y = 0

हम इस समीकरण को इस तरह भी लिख सकते हैं:
2⁴ x -(1+2+2²+2³) y = 0

अब अगर देवताओं की संख्या चार के बजाए 'N' हो तो इस समीकरण का सामान्य स्वरूप कुछ ऐसा होगाः
2^N x -(1+2+2²+2³+ ...+2^N-1) y = 0

यहां पर थोड़े से कठिन गणित की जरूरत होगी। कोष्ठक के अंदर की संख्या ‘N' राशियों वाली एक गुणोत्तर श्रेणी ( ज्योमेट्रिक श्रृंखला ) है जिसमें सभी राशियों के बीच 2 का अनुपात है। इस तरह की श्रृंखला का जोड़ इस प्रकार भी लिखा जा सकता है:
1+2+2²+2³+...+2^N-1 = ( 2^N-1 )/( 2-1 )

कोष्ठक की राशि का मान रखने के पश्चात पहले वाला समीकरण इस प्रकार होगाः
2^Nx - (2^N-1) y / (2-1) = 0

इस समीकरण का सबसे छोटा पूर्णांक हल अब पहले की तरह निकाला जा सकता है:
X = (2^N-1) / (2-1)  और y = 2^N

समीकरण के नीचे वाले हिस्से को हमने सरल बनाकर 'एक' जानबूझ कर नहीं लिखा है, क्योंकि अब हम समीकरण के सामान्यीकरण का अगला कदम उठाने वाले हैं कि अगर हर बार फूलों की संख्या दुगनी होने के बजाए 'n' गुनी हो जाए तो ऐसी स्थिति में हमें इस समीकरण में हर जगह '2' के स्थान पर 'n' लिखना होगाः
X= (n^N-1) / (n-1) और y = n^N

यही होगा पहेली का हल अगर देवताओं की संख्या 'N' हो और हर बार तालाब के जादुई पानी में फूलों की संख्या 'n' गुनी होती जाए। यहां पर भी हमने वही माना है कि पुजारी ने 'x' फूल तोडे हैं और ‘y' फूल हर बार देवता को चढ़ाए। हल पर विश्वास न हो तो आप खुद एक बार आज़माकर ज़रूर देख लीजिए।

हल द्विअंकीय पद्धति से
एक बार फिर उसी पहेली से शुरू करते हैं - चार देवता और जादुई पानी जो फूलों की संख्या दुगनी कर देता है। इस बार देखते हैं कि द्विअंकीय पद्धति का इस्तेमाल करते हुए इस पहेली को कैसे हल किया जा सकता है। जो तरीका अपनाने वाले हैं वो समझ में आ जाए इसलिए सबसे पहले द्विअंकीय पद्धति और दशमलव पद्धति के बीच के संबंध को समझ लेते हैं।

जबकि दशमलव पद्धति में अंकों को दर्शाने के लिए 10 अलग अलग संकेत होते हैं, द्विअंकीय पद्धति में केवल दो ही संकेत पर्याप्त होते हैं  -0 और 1 जब हम दशमलव पद्धति में कोई अंक लिखते हैं तो पहले स्थान का मान 10⁰ = 1 होता है, दूसरे स्थान का मान 10¹ = 10 होता है, तीसरे स्थान का मान 10² = 100, चौथे का 10³ = 1000, और इसी तरह आगे भी।

इस की तुलना में द्विअंकीय पद्धति में स्थानीय मान इस प्रकार  होते हैं: 2⁰ = 1,  2¹ = 2,  2² = 4, 2³ = 8, . . . ऐसे ही आगे भी। इसलिए द्विअंकीय पद्धति में अंक एक, दो, तीन, चार, पांच, छ, सात, आठ, नौ, . . . इत्यादि को क्रमशः इस प्रकार लिखा जाता है: 0, 1, 10 (द्वि), 11 (द्वि), 100 (द्वि), 101 (द्वि), 110 (द्वि), 111 (द्वि), 1000 (द्वि), 1001 (द्वि), . . . आगे भी यह दर्शाने के लिए कि हम कौन-सी पद्धति अपना रहे हैं, हम यही तरीका इस्तेमाल करेंगे; जब भी अंक द्विअंकीय पद्धति में लिखे गए हों तो कोष्ठक में 'द्वि' (द्वि) लिखेंगे।

इसलिए आठ को या तो 8 लिखा जाएगा, या फिर 1000 (द्वि)। द्विअंकीय पद्धति में भी चारों गणितीय क्रियाएं उसी तरह से की जाती हैं जैसे कि दशमलव पद्धति में, फर्क केवल इतना ही होता है कि द्विअंकीय पद्धति में 2 हो जाने पर हासिल ले जाना होता है, जबकि दशमलव पद्धति में 10 होने पर ही हम हासिल लेकर जाते हैं। एक और फर्क है कि दशमलव पद्धति में 10 से गुणा करने पर हम संख्या के दाहिनी तरफ एक शून्य जोड़ देते हैं, द्विअंकीय पद्धति में किसी भी संख्या को 2 से गुणा करने पर ऐसा करना होगा।

द्विअंकीय पद्धति से इस संक्षिप्त परिचय के पश्चात अब हम तालिका-1 देख सकते हैं जिसमें दशमलव और द्विअंकीय, दोनों पद्धतियों में इस पहेली के उत्तर लिखे गए हैं। इस तालिका में चार स्थितियों पर गौर किया गया है. अगर पहेली में देवताओं की संख्या एक हो, दो हो, तीन हो या चार हो तो जवाब क्या होंगे। हर स्थिति में जादुई पानी फूलों को दुगना कर देता है।

तालिका-1

द्विअंकीय पद्धति में हल देखें। जितनी भी देवताओं की संख्या है जिनको चढ़ावा चढ़ाना है, उतनी बार 1 लिखने से तोड़े गए फूलों की संख्या मिल जाती है; और देवता को चढ़ाए गए फूलों की संख्या पता करने के लिए 1 के बाद उतनी बार शून्य लगाने पड़ते हैं।

केवल एक देवता वाली पहेली का हल देखें। 1 फूल तोड़ा जाता है जो पानी में धोने पर दो यानी कि 10 (द्वि) में बदल जाता है। और उन्हें देवता को चढ़ा दिया जाता है।

अगर पहेली में दो देवता हों तो तीन फूल तोड़े जाते हैं यानी कि 1 1 (द्वि) जो धोने पर 6 यानी कि 1 10 (द्वि) फूलों में तब्दील हो जाते हैं। इनमें से चार यानी 100 (द्वि) फूल पहले देवता को चढ़ाने पर दो यानी 10 (द्वि) फूल बचे जो पानी से धोने पर चार यानी 100 (द्वि) में बदल गए, उतने ही जितने दूसरे देवता को चढ़ाने के लिए चाहिए थे।

हर बार जब फूलों को पानी में धोने और एक देवता को चढ़ा देने का चक्र पूरा होता है, बचे हुए फूलों की संख्या में सबसे दाहिनी ओर का ‘एक 'शून्य' में बदल जाता है। पहेली में जितने देवता हों उतनी बार 'एक' ‘शून्य' में बदलते जाते हैं।

द्विअंकीय जवाब में तोड़े हुए और चढ़ाए गए फूलों की संख्याएं इतने सरल रूप में इसलिए आती हैं क्योंकि हर बार पानी में डूबाने पर फूलों की संख्या दुगनी हो जाती है, वैसे ही जैसे कोई भी द्विअंकीय संख्या दाहिनी ओर अंत में शून्य लगाने पर दुगनी हो जाती है। अब सवाल यह उठता है कि दशमलव पद्धति में भी क्या जवाब ऐसे सरल रूप में सामने आएंगे अगर पानी में ऐसा जादू हो कि उसमें धोने पर फूलों की संख्या दस गुनी हो जाए?

अगर पहेली में एक ही देवता है तो चलिए जांच करते हैं कि इसमें भी जवाब 1 और 10 होगा क्या याद रखिए कि यहां पर अब अंकों को दशमलव पद्धति में दर्शाया जा रहा है, और पानी फूलों को दस गुना कर देता है। एक फूल तोड़ा, जादुई पानी ने उसे 10 फूलों में बदल दिया। इन 10 फूलों को देवता को चढ़ा दिया। अभी तो सरल जवाब मिल रहा है। अब देवताओं की संख्या बढ़ा कर देखते हैं।

अगर दो देवता हैं तो जवाब 11 और 100 होना चाहिए। तोड़े हुए 11 फूलों को धोने पर उनकी संख्या दस गुनी यानी कि 110 हो जाएगी और इनमें से जब पहले देवता को 100 फूल चढ़ा दिए जाते हैं तो 10 फूल शेष रहते हैं। धोने पर ये फूल दस गुना अर्थात 100 बन जाते हैं जिन्हें दूसरे देवता को चढ़ा दिया जाता है।

ऐसे और भी आगे बढ़ते जाने पर समझ में आता है कि हमारा अंदाजा सही निकल रहा है। देखिए अब हम इस पहेली के एक अचंभित कर देने वाले सामान्यीकरण की तरफ बढ़ गए हैं। अगर देवताओं की संख्या 'N' हो और जादुई पानी फूलों को 'n' गुना बना देता हो तो पहेली का हल यानीः

तोड़े हुए फूलों की संख्या x = 111... 1 (n) होगी

और देवता को चढ़ाए गए फूलों की संख्या y = 100... (n) होगी।

यहां पर 'x' संख्या में 'N' बार 1 आएगा और 'y' संख्या में 1 के बाद 'N' शून्य आएंगे। और इन अंकों को n-अंकीय पद्धति में पढ़ना होगा; यानी कि फूल दुगने हो रहे हैं तो द्विअंकीय पद्धति में, तिगुने हो रहे हैं तो त्रिअंकीय पद्धति में, . . . और दस गुने हो रहे

हैं तो दशमलव पद्धति में।

बिहार-तमिलनाडु की पहेलियों में समानता क्यों
हम उस पहेली से बहुत दूर निकल आए हैं जो हमारे गांव के पुश्तैनी नाई ने पूछी थी। यह सब कुछ यह बताने के लिए लिखा कि बहुत से रास्ते एक ही मंजिल तक पहुंच सकते हैं; और अक्सर हर रास्ते की अपनी खूबियां होती हैं, दिलचस्प नज़ारे होते हैं। इसीलिए गणित की कक्षा में हमें कोशिश करनी चाहिए कि बच्चे एक ही सवाल को तरह-तरह से हल करने की कोशिश करें, उन्हें इस बात के लिए विशेष रूप से प्रोत्साहित करना चाहिए। यही नहीं, यह देखते हुए कि पहेलियों और बुझावतों में हम सब कितना रस लेते हैं, कितना समय लगाते हैं उन्हें हल करने में, और कितनी कोशिश करते हैं; मुझे सदा ताज्जुब होता है कि कक्षा में गणित पढ़ाने के लिए उनका इस्तेमाल क्यों नहीं किया जाता।

एक और कारण है जिस वजह से मैंने ये लेख लिखना तय किया, हाल ही में मैंने एक पुस्तक में तमिलनाडु की यह पहेली पढ़ीः

"बाजार जाते समय एक तेल का व्यापारी विनायक मंदिर के सामने से गुजरा और उसने यह मन्नत मानी कि अगर उसकी बिक्री अच्छी हुई तो वह कुछ तेल चढ़ावे में देगा। उसने इसी तरह की मन्नत देवी और अय्यनार के मंदिरों पर भी की। काफी सफल बिक्री के पश्चात घर लौटते हुए वो चढ़ावा चढ़ाने से पहले स्नान करने के लिए अय्यनार के मंदिर पर रुका। जब वो नहा रहा था तो एक कौए ने उसका तेल का बर्तन लुढ़का दिया जिससे अधिकतर तेल गिर गया। व्यापारी मंदिर में गया और उसने देवता से क्षमा मांगी कि वो अपनी मन्नत पूरी नहीं कर पा रहा है। उसकी भक्ति से प्रसन्न होकर अय्यनार ने बर्तन में बचे हुए तेल की मात्रा को दुगना कर दिया और व्यापारी चढ़ावा चढ़ाने की अपनी मन्नत पूरी कर पाया।"

अब व्यापारी देवी के मंदिर में गया, उसने देवी को पूरा किस्सा सुनाया और अपना वायदा पूरा न कर पाने के लिए क्षमायाचना मांगी क्योंकि उसके पास पर्याप्त तेल नहीं बचा था। देवी ने भी बर्तन में बचे हुए तेल की मात्रा दुगनी कर दी और व्यापारी वहां भी उतना ही चढ़ावा चढ़ा पाया। विनायक के मंदिर में भी ऐसा ही हुआ, तेल की मात्रा दुगनी हो गई और उसने मन्नत पूरी की: उसके बाद उसके पास ज़रा-सा भी तेल नहीं बचा।

अब सवाल यह है कि कौए के बर्तन पलटा देने के बाद उस बर्तन में कितना तेल बचा था?''

यह स्पष्ट है कि यह पहेली और हमारे गांव के पुश्तैनी नाई ने बुझाई पहेली एक जैसी ही हैं, केवल अंतर इतना है कि तमिलनाडु की पहेली में तीन ही देवता हैं और जवाब पूर्णांक में हो यह ज़रूरी नहीं है। स्वाभाविक सवाल है कि दो पहेलियां, एक बिहार से व दूसरी तमिलनाडु से, जो हजार किलो मीटर से भी ज्यादा दूर हैं एक दूसरे से, इतनी एक समान कैसे हैं? क्या अन्य राज्यों व भाषाओं में भी ऐसी पहेलियां पाई जाती हैं? क्या यहां जो तरीके सुझाए गए हैं। उनके अलावा भी और कुछ तरीके हैं इन्हें हल करने के? अगर इन सवालों पर आप भी रौशनी डाल सकें तो मुझे अच्छा लगेगा।

विजय शंकर वर्मा - दिल्ली विश्वविद्यालय में भौतिक शास्त्र पढ़ाते है।