प्राचीन भारत में रेखागणित

रामकृष्ण भट्टाचार्य

इस अंक से शुरू हुआ यह आलेख छह अंकों में प्राचीन भारत में रेखागणित के विभिन्न पहलुओं की विस्तृत जांच-पड़ताल करेगा। रेखागणित की शुरुआत के बारे में उपलब्ध जानकारियों का विश्लेषण करते हुए विभिन्न संभावनाओं को टटोला गया है इस पहली कड़ी में।

I  रेखागणित शुरुआत कहां

प्राचीन भारत में रेखागणित की शुरुआत कैसे हुई यह जानने के लिए पहले हमें कुछ गलतफहमियों से मुक्त होना होगा। पहले तो इस सोच को बदलना होगा कि संसार में सिर्फ एक और सिर्फ एक ही रेखागणित होता है। और वह है ग्रीक (यूक्लीडियन) रेखागणित। यदि ऐसा होता, तो हमें यह विश्वास करना पड़ता कि सर्वाधिक महत्वपूर्ण इमारतों और नियोजित शहरों का निर्माण करने वाले मिस्र निवासियों, बेबीलोनियाइयों और भारतीयों को रेखागणित की जानकारी नहीं थी; जबकि ग्रीकों ने किसी चमत्कार से शून्य में से रेखागणित को जन्म दे दिया।

यहां तक कि यूरोप और संयुक्त राज्य अमेरिका के श्रेष्ठ विद्वानों का भी यही ख्याल रहा है। प्रमुख वैज्ञानिकों और विज्ञान के इतिहासकारों द्वारा बार-बार यह दावा किया गया है कि पश्चिमी विज्ञान के विकास के लिए एक अति महत्वपूर्ण तत्व ‘‘ग्रीक दार्शनिकों के द्वारा औपचारिक तार्किक प्रणाली (यूक्लीडियन रेखागणित में) का आविष्कार' रहा है। ऐसा अलबर्ट आइन्स्टीन ने कहा था। इस पर जोसफ नीढम जो चीन के विज्ञान और सभ्यता के विशेषज्ञ हैं ने जवाब दियाः

"आइन्स्टीन खुद यह स्वीकार करने वाले पहले व्यक्ति होते कि वे चीनी, संस्कृत और अरबी संस्कृतियों में विज्ञान के विकास के बारे में कोई ठोस जानकारी नहीं रखते। वे सिर्फ यह जानते हैं कि उनमें आधुनिक विज्ञान का विकास नहीं हुआ था और इस अदालत में उनकी महान प्रतिष्ठा को साक्षी के रूप में पेश नहीं किया जाना चाहिए। इन सब मूल्यांकनों से मैं अपने आपको बिल्कुल सहमत नहीं पाता हूं।''

यह ज़रूर है कि भारत में जो रेखागणित है वह ग्रीस के रेखागणित के समान नहीं है। पर हमें यह ध्यान रखना चाहिए कि।
---आधुनिक विज्ञान के जन्म के काफी पहले एशिया और यूरोप में प्राचीन काल में और मध्यकाल में विज्ञान था। और,
---एशियाई संस्कृतियों में विज्ञान सैद्धांतिक की अपेक्षा उपयोग आधारित ज्यादा था, पर इससे वह कम वैज्ञानिक नहीं हो गया।

दूसरी ओर, यूक्लीडियन रेखागणित के मूल्य को ज्यादा आंकने के बारे में जो कुछ नीढम ने कहा है वह चिंतन करने लायक हैः

"हालांकि विज्ञान के इतिहासकार पश्चिमी जगत के प्रति की गई यूक्लीडियन रेखागणित की सेवा का प्रशस्तिगान करते नहीं थकते, मुझे बॉन के डॉ. पाल लोरेन्जन से 1949 में हुआ वार्तालाप खूब याद है, जिसमें उन्होंने यह मत जाहिर किया था कि यूरोप के भले कि लिए जितना रेखागणित काफी होता उससे ज्यादा रेखागणित यूरोप के पास था। इसमें शक नहीं कि रेखागणित आधुनिक विज्ञान के लिए अनिवार्य आधार था लेकिन उसका एक खराब असर यह हुआ कि वह हमें हर तरह के अमूर्त समयातीत स्वयंसिद्ध साध्यों पर विश्वास करने के लिए उकसाता है और कठोर तार्किक और धर्मशास्त्रीय कथनों को स्वीकार करने के लिए भी हमें उकसाता है।''

इसलिए हम इस अनुमान के साथ शुरू करना पसंद करते हैं कि प्राचीन मिस्र, बेबीलोनिया और भारत के पास भी उनका अपना रेखागणित था जो राजगीरों और बढ़इयों के वास्तविक काम से लिया गया था।

राजगीर और बढ़ई क्यों? क्या रेखागणित मिस्र में जमीन नापने की क्रिया से पैदा नहीं हुआ जैसा कि माना जाता है? ग्रीक शब्द ज्योमेट्रिया खुद यह सुझाता है। ‘जे' ( जिया का संक्षिप्त रूप ) का अर्थ है पृथ्वी या भूमि, और ‘मेट्रिया' का मतलब है मापन। इसी से इस शब्द का दूसरा अर्थ निकला - "गणित की वह शाखा जिसका संबंध बिंदुओं, रेखाओं, तलों और ठोस के लक्षणों और संबंधों से है।'' (जैसा कि कन्साइज़ ऑक्सफोर्ड डिक्शनरी परिभाषित करती है)।

पांचवीं सदी का ग्रीक इतिहासकार हेरोडोटस कहता है कि मिस्र ने यूनानियों को रेखागणित का ज्ञान दिया। कहा जाता है कि मिस्र के शासक सेसोस्ट्रिस (रेमेसिस द्वितीय लगभग 1347 ई. पू.) ने सभी मिस्र निवासियों को बराबर-बराबर वर्गाकार भूमि देकर पूरे देश को मिस्र निवासियों में बांट दिया था और यही उसकी आय का स्रोत था। उसने इस आधार पर सालाना कर तय किया था। यदि किसी व्यक्ति की भूमि का कुछ हिस्सा नील नदी के बहाव में आ जाता था तो वह व्यक्ति राजा को बताता था कि उसकी भूमि का क्या हुआ। तब राजा अपने आदमियों को यह नापने भेजता था कि उस व्यक्ति की कितनी भूमि कम हो गई है जिससे भूमि के आकार के अनुसार कर तय किया जा सके। हेरोडोटस कहता है, “मेरा विचार है कि इससे यूनानियों ने भूमि को नापने (ज्यामेट्रिया) की कला सीखी।''

इस अंश का अक्सर संदर्भ दिया गया है और इसे बहुधा उद्धरित किया गया है। यह कम-से-कम इस बात को प्रकट करता है कि यूनानियों ने यह दावा कभी नहीं किया कि रेखागणित उनका आविष्कार है। उन्होंने स्वीकार किया है कि रेखागणित मिस्र से आयातित की गई। तथापि, हमें हेरोडोटस के कथन के इस वाक्यांश पर भी ध्यान देना चाहिए, “मेरे विचार से।'' वह सामान्य इतिहासकार था जो युद्ध और राजनीति में रुचि रखता था, विज्ञान में नहीं। उसके निष्कर्ष शायद बहुत विश्वसनीय नहीं भी हों।

ऐसा ही है पर, प्रोक्लस (410 485 ई.) भी यही कहानी कहता है। उसने यूक्लिड के एलीमेन्ट्स (300 ई.पू.) पर एक टीका लिखी और इस कारण वह जानता था कि वह किसके बारे में बोल रहा है। प्रोक्लस का बाद के काल का होना उसका मत मानने के रास्ते में बाधा नहीं बनना चाहिए। कहा जाता है कि उसे चौथी सदी ई. पू. में लिखे यूडेमस के गणित के इतिहास से यह जानकारी मिली थी। दुर्भाग्य से वह कृति अब उपलब्ध नहीं है।

मिस्र भूमि मापन और इसलिए गणित का मूल स्रोत था - इस गाथा का समर्थन डायोजिनीस लेरटियस (लगभग 300 ई. पू.) द्वारा लिखित ‘डेमोक्रिटस नामक दार्शनिक (लगभग 300 ई. पू.) की जीवनी' भी करती है। कहा जाता है कि अणु सिद्धांत के इस प्रारंभिक प्रतिपादक ने पुरोहितों से रेखागणित सीखने के लिए मिस्र का भ्रमण किया था।

डेमोक्रिटस एक महान चिंतक था पर किसी भी सूरत में वह विनम्र व्यक्ति नहीं था। उसकी कृति के बचे अंश (उसकी कोई भी पूरी कृति प्राप्त नहीं हुई है) में वह घोषित करता है:

"मैंने अपने ज़माने के किसी भी व्यक्ति से ज्यादा भ्रमण किया है और बहुत विस्तार से जांच पड़ताल की है; और ज्यादातर देश और इलाके देखे हैं और कई विद्वानों को सुना है और प्रमाणसहित शोध-प्रबंध लिखने में कोई भी मुझसे बढ़कर नहीं है। यहां तक कि मिस्र का तथाकथित आरपेडोनाप्टे भी नहीं। उसके साथ मैंने विदेशी भूमि में पांच साल गुज़ारे।'

‘आरपेडोनाप्टे' (ग्रीक भाषा में 'हरपेडोनाटाई', का शब्दिक अर्थ है - ‘रस्सी खींचने वाले') प्राचीन मिस्र के भूमिमापक या सर्वेअर थे। ज्योमीटर्स को भी शायद इसी नाम से पुकारा जाता था। इसलिए भूमि मापन और गणित की इस शाखा (रेखागणित) के आपसी संबंध का भाषाशास्त्रीय और ऐतिहासिक प्रमाण है।

डेमोक्रिटस के खुद के शब्दों से ऐसा लगता है कि मिस्र के निवासियों ने यूक्लिड (300 ई. पू.) के बहुत पहले रेखागणितीय साध्यों की तार्किक व्यवस्था कर ली थी या यूक्लिड के पूर्ववर्तियों जैसे कि चिआस के हिप्पोक्रेट (लगभग 430 ई. पू.) ने भी ऐसा करने की कोशिश की थी। इस प्रकार खुद यूनानियों की कृतियों के द्वारा यूनानी चमत्कार की गाथा रद्द हो जाती है।

II  रेखागणितः शुरुआत किसने की

जो भी हो, भूमिमापन से रेखागणित के जन्म की कहानी का समर्थन ऊपर उल्लेखित सभी विद्वान करते हैं। फिर हम भूमि मापने वालों के स्थान पर राजगीरों और सुतारों की बात क्यों करते रहे।

विख्यात पुरातत्वशस्त्री वी. गॉर्डन चाइल्ड (1892-1957) ने सबसे पहले रेखागणित के जन्म के बारे में प्रचलित मत को चुनौती दी। वे बेबीलोनिया और मिस्र के विद्यमान दस्तावेज़ों की समीक्षा करने के बाद 1936 में निम्नलिखित निष्कर्ष पर पहुंचेः

"हमारे पास जो प्रमाण हैं उनसे इस सिद्धांत का समर्थन नहीं होता कि सटीक रेखागणित मिस्र या बेबीलोनिया में भूमि मापन से उत्पन्न हुई।''

चाइल्ड ने ऐसा क्यों कहा? वे यह अस्वीकार नहीं करते कि ये दस्तावेज़ बुनियादी रेखागणित का ज्ञान प्रदर्शित करते हैं, खासकर खेतों में बोने के लिए लगने वाले बीज और उनसे प्राप्त होने वाले लगान के अनुमान के लिए खेतों के क्षेत्रफल के सिलसिले में। लेकिन वे कहते हैं - "ऐसे अनुमानों के लिए पूरी तरह सटीक होना जरूरी नहीं था; कारिंदा मोटे तौर पर सिर्फ यह जानना चाहता था कि प्रत्येक खेत के लिए कितना उत्पादन माना जाए; कर एकत्र करने वाले अधिकारी को संभावित फसल का एक मोटा अनुमान ही चाहिए था।''

तो फिर सटीक विचारों और पूर्णतः सही मापन की ज़रूरत किसे होगी? चाइल्ड का कहना था, वास्तुकारों और इंजीनियरों को। “अपना काम संपन्न करने के लिए बहुधा उन्हें ही अत्यंत शुद्ध हिसाब की जरूरत थी। पिरामिड का सटीक होना कर्मकांड की दृष्टि से अत्यंत महत्व का था। मिस्र के लिपिकों ने पिरामिड के एक खंड का आयतन जानने के लिए सही सूत्र खोज निकाला और उसका उपयोग किया।'' चाइल्ड अपने मत के समर्थन में मॉस्को पेपीरस में प्राप्त गणित के एक सवाल का उल्लेख करते हैं।

डब्लू डब्लू. सॉयर, अपनी रोचक किताब ‘मेथेमेटिशियन्स डिलाइट' (1943) में भी इसी निष्कर्ष पर स्वतंत्र रूप से पहुंचते हैं, (किसी भी रूप में वे चाइल्ड का उल्लेख नहीं करते)। वे ज़ोर देकर कहते हैं, "शुरुआती गणितज्ञ थे व्यावहारिक लोग यानी सुतार और भवन निर्माता।''

उन्होंने अंग्रेजी भाषा से कुछ रोचक भाषाशास्त्रीय प्रमाण की ओर ध्यान खींचा। उन्होंने कहा, “इस तथ्य ने जियोमिति में प्रयुक्त किए जाते शब्दों पर अपनी छाप छोड़ी है। ‘सीधी रेखा (स्ट्रेट लाइन) क्या है? यदि ‘सीधी' (स्ट्रेट) शब्दकोष में देखें तो आप पाएंगे कि यह ‘स्ट्रेच्ड' (खिंचा हुआ) के लिए पुराने शब्द से आया है; जबकि ‘लाइन' (रेखा) शब्द लिनेन' या ‘लाइन थ्रेड के समान ही है। तो एक स्ट्रेट लाइन यानी स्ट्रेच्ड लिनेन थ्रेड यानी खिंचा हुआ सूती धागा है - जैसा कि कोई भी आलू खोदने वाला या ईट जमाने वाला जानता है।''

इस तरह चाइल्ड द्वारा उल्लेखित वास्तुकारों और इंजीनियरों के अलावा सुतारों को भी रेखागणित को जन्म देने में योगदान करने वाले मान सकते हैं।

एक विख्यात भौतिकशास्त्री और ‘साइंस इन हिस्ट्री' पुस्तक के लेखक जे. डी. बरनाल (1901-71) ने चाइल्ड और सॉयर के मतों का पूरी तरह समर्थन किया है। उन्होंने कहाः

"संभवतः भूमि मापन के पहले ही निर्माण के काम ने रेखागणित की नींव स्थापित होने में योगदान दिया। शुरू में कस्बों की इमारतें सिर्फ गांव के झोपड़ों जैसी ही थीं जो लकड़ी और घास-फूस के बनते थे। नगर की सीमित जगह में आग के बढ़ते खतरे को देखते हुए इनकी जगह मिट्टी का इस्तेमाल एक बड़ा सुधार था। अगला जो कदम उठा वह इससे भी ज्यादा महत्वपूर्ण थाः सांचे में बनाकर, धूप में सुखाई गई ईंट। ईंट संभवतः कोई मौलिक खोज नहीं थी। शायद वह पहाड़ों में घर बनाने के लिए प्राकृतिक रूप से मिलने वाली पत्थर की सिल्लियों का मिट्टी में बना प्रतिरूप था। घाटियों में पत्थर न होने के कारण मिट्टी से काम चलाना पड़ता था।"

ईंटें तभी सुविधा से एक के ऊपर एक जमाई जा सकती हैं जब वे आयताकार हों। और उनके उपयोग से समकोण का विचार और सीधी रेखा का उपयोग शुरू हुआ। यानी स्ट्रेट लाइन -- बुनकर या रस्सी बनाने वाले की खिंची हुई रेखा।''

बरनाल एक चित्र प्रस्तुत करते हैं। जिसमें 1470 ई. पू. के लगभग की रस्सी बनाने, ईंट बनाने, आदि की मिस्र की तकनीकें बताई गई हैं।

गणित का जन्म स्थान कहे जाने वाले मिस्र का यह ऐतिहासिक प्रमाण निष्कर्षतः यह प्रमाणित करता है कि रेखागणित राजगीरों की जरूरतों के कारण आवश्यक हो गई थी, न कि कारिंदों की जरूरतों के कारण। दस्तकारों के नाप में सटीकता की ज़रूरत थी।

ऊपर जो कुछ कहा गया है उसके आधार पर हम यह धारणा त्याग सकते हैं कि ग्रीक शब्द ज्यामेट्रिया की व्युत्पत्ति गणित की इस शाखा के उद्गम की पूरी कहानी बताती है।

बेंजामिन फेरिंग्टन अपनी ‘ग्रीक साइंस' में लिखते हैं कि विज्ञान की हर शाखा का उद्गम लोगों की व्यावहारिक जरूरतों से हुआ है और रेखागणित उसमें अपवाद नहीं है। यूक्लिड ने जिस प्रकार, व्यवहार से अलग करके, राजगीर और सुतार के ज्ञान को व्यवस्थित रूप दिया है, उससे उसके विकास का सही क्रम प्रकट नहीं ।

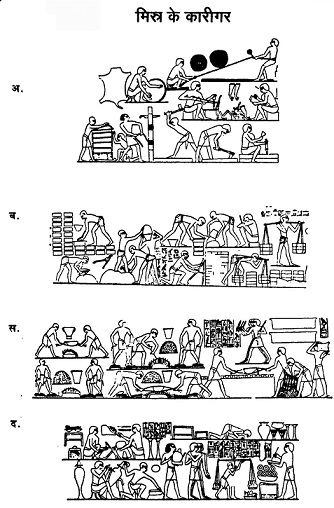
मिस्र के कारीगरः आज से लगभग साढे तीन हजार साल पहले विविध कामों में जुटे हुए मिस्र के कारीगर। अ. रस्सी बटाई तथा बढ़ईगिरी का काम करते कारीगर। इसमें कारीगरों द्वारा इस्तेमाल किए जा रहे औजारों पर गौर करें। ब. ईंटों को बनाने का काम बड़े पैमाने पर किया जा रहा है। साथ ही विविध औजारों की मदद से भवन का निर्माण कार्य भी चल रहा है। स. कांसे को ढाल कर विविध सामान बनाते हुए कारीगर। द. बेशकीमती धातुओं से आभूषण बनाने वाले कारीगर। साथ ही एक तराजू की मदद से तौलने का काम भी चल रहा है। गौर करें कि इन चित्रों में तराजू और ईंटों को ढोने वाले कांवर में काफी समानता है।

होता। दूसरी ओर, समतलीय रेखागणित (यूक्लिड के एलीमेंट्स के मॉडल की तर्ज पर) की पाठ्यपुस्तकें हमें सिर्फ यूनानियों के नतीजों के बारे में बताती हैं - परंतु यह नहीं कि यूनानी ये सब बेबिलोन और मिस्र के कारीगरों की उपलब्धियों के आधार पर कर पाए। गॉर्डन चाइल्ड कहते हैं। कि - "बेबिलोनियाई और मिस्री लोगों ने रेखागणित के नियम प्राप्त कर लिए थे जो एकदम ठीक थे किंतु वे अमूर्त जगह (Space) के गुणधर्मों से अनुभव निरपेक्ष ढंग से नहीं निकाले गए थे, जैसा कि यूक्लिड की रेखागणित में होता है। ऐसे ‘शुद्ध रेखागणित' के लिए कोई साक्ष्य नहीं मिलते।''  

सॉयर शुद्ध तार्किक प्रणाली के रूप में रेखागणित को पढ़ाए जाने के तरीके की आलोचना करते हैं जिसमें बिंदुओं, रेखाओं, आकृतियों की परिभाषा से शुरू करके, स्वयं सिद्ध कथनों से चलते हुए, प्रमेयों और सवालों तक जाते हैं। उनके मत में, “बच्चों से यह उम्मीद करना अन्याय है कि वे उस रूप में रेखागणित का अध्ययन करना शुरू कर दें जैसा हमें यूक्लिड ने दिया था।" रेखागणित ईसा के पहले चौथी सहस्राब्दी में पिरामिड बनाने की कला के साथ शुरू हुई। इस प्रकार मिस्र में महान पिरामिडों के निर्माण (3900 ई. पू.) और यूक्लिड के एलीमेंट्स (300 ई. पू.) के बीच करीब 3600 वर्षों का अंतर है। वे कहते हैं, “हम मानव के प्रयासों के 3600 वर्षों को इतनी आसानी से नहीं लांघ सकते।''

सॉयर कहते हैं, "रेखागणित सीखने

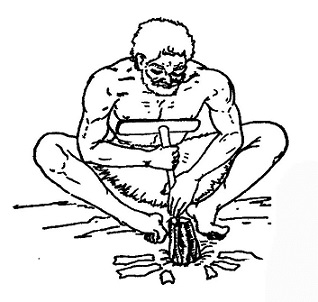पाषाण कालीन कारीगर पत्थर से औज़ार बनाता हुआ।
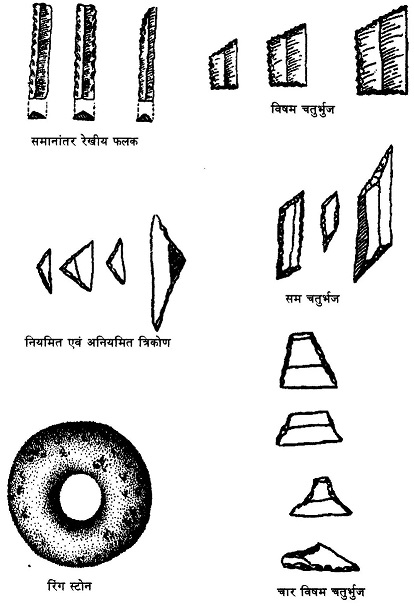
अगले पृष्ठ पर पाषाण कालीन औज़ारों में से कुछ रेखागणितीय आकृतियों को दिखाया गया है।

का सबसे अच्छा तरीका उस रास्ते पर चलना है जिस पर मानव जाति चली - चीजें करो, चीजें बनाओ, चीजों को देखो, चीजें व्यवस्थित करो और फिर चीजों के बारे में तर्क करो।" असल में इसी तरीके से रेखागणित विकसित हुआ। ग्रीक रेखागणित ही संसार में एकमात्र रेखागणित नहीं है। ‘अमूर्त जगह' की अवधारणा बनने के लिए, पत्थर की फर्शियों, ईंटों आदि ठोस चीजों के साथ कुछ प्रयोग की पूर्व पीठिका की जरूरत है। इसलिए शुरुआती श्रेय रेखागणित संभव बनाने वाले विद्वानों से ज्यादा श्रमिकों को दिया जाना चाहिए।

III  हड़प्पा संस्कृति में रेखागणित

हमें इस गलतफहमी को भी दूर करना होगा कि भारत का इतिहास वेदों से शुरू होता है। वैदिक काल (1800 ई. पू. से 500 ई. पू.) के हजारों साल पहले ही इस उपमहाद्वीप में लोग रहते आए हैं। यहां पाषाण काल से लोग रहते आए हैं और संस्कृति को आगे बढ़ाते रहे हैं।

हालांकि ठोस चीजों को देखना, व्यवस्थित करना और बनाने का सिलसिला पुरापाषाण काल से चला आ रहा है, अमूर्त ज्यामितीय आकृतियों का उपयोग उत्तर पाषाणकाल से देखने को मिलता है। उत्तर पाषाण काल के औजारों में समानान्तर रेखाएं, त्रिकोण, ट्रेपिज, समचतुर्भुज, वृत्त आदि आकृतियों का इस्तेमाल है यानी वे लोग इन आकृतियों को पहचानते थे व इनके गुण एवं उपयोग से भी वाकिफ थे। इस काल के शैलचित्रों व अन्य अवशेषों पर बनाई कलाकृतियों में भी ज्यामितीय आकृतियों का काफी इस्तेमाल किया गया है।

इन उदाहरणों से यही निष्कर्ष निकलता है कि रेखागणित की शुरुआत औजार बनाने वालों व चित्रकारों से हुई है। उल्लेखनीय है कि केवल भारत में ही नहीं बल्कि पूरे विश्व में यही क्रम पाया जाता है।

वैदिक बस्तियां बसने के काफी पहले भारत में शहरी सभ्यता के विकसित केन्द्र थे। हमारा मतलब हड़प्पा संस्कृति के लोगों से है। पुरातत्वविद लगभग 2500 ई. पू. की सिन्धु घाटी सभ्यता को हड़प्पा संस्कृति कहते हैं। यह सभ्यता वर्तमान अफगानिस्तान, पाकिस्तान और भारत में दूर-दूर तक फैली थी। यद्यपि हम एक सांस में मोहंजोदड़ो और हड़प्पा का उच्चारण करते हैं, यह याद रखना हितकर होगा कि वे एक-दूसरे से करीब 592 किलोमीटर दूर हैं। इसी प्रकार गुजरात में खम्भात की खाड़ी के उत्तर में स्थित लोथल और हिमालय की तराई में रोपड़ के बीच की सीधी दूरी लगभग 1152 किलोमीटर है।

इतनी सारी खुदाइयों और विस्मयकारी खोजों के बावजूद ये स्थल मूक साक्षी ही हैं। सिंधुलिपि अभी भी संतोषजनक ढंग से नहीं पढ़ी गई है।

वैसे सिंधु लिपि को पढ़ लिया जाए तो भी शायद बहुत ज्यादा मदद नहीं मिलेगी क्योंकि ज्यादातर शब्द सीलों पर अंकित हैं - इनसे रेखागणित के बारे में जानकारी मिलना कठिन है। फिर भी खुदाई में कई औज़ारों के अवशेष मिले हैं जो हमारे काम के हैं। वे हमें एक बहुत रोचक कहानी सुनाते हैं। हमें उसका पुनर्निर्माण करना है।

लोथल में हुई खुदाई में हमें राजगीर के कई औज़ार मिले हैं। पहला औज़ार मिट्टी का बना साहुल (Plum-bob) है। इस तरह के दो औज़ार हैं -- एक में ऊध्र्वाकार (Vertical) छेद है जिससे धागा पिरोकर उसे लटकाया जाता था; और दूसरे में सिरे पर चुंडी में बने क्षैतिज छेद से धागा पिरोकर लटकाया जाता था। घुंडी के ऊपर एक छिद्रयुक्त बेलन (Perforated Terracota Cylinder) रखा जाता था।

इसी प्रकार, शंख की एक पोली बेलनाकार चीज़ मिली है जिसे कम्पास के रूप में पहचाना गया है। उसमें छेद हैं - चार ऊपर और चार नीचे। ऐसा अनुमान लगाया गया है कि यह औज़ार

आधुनिक Cross Staff का काम करता था। यह "45 डिग्री, 90 डिग्री, 180 डिग्री और 360 डिग्री तक के अन्य कोण बनाने के लिए काम में लाया जा सकता था। आमने-सामने के छेदों से दिखने वाले बिंदुओं को जोड़ने से बनी सीधी रेखाएं एक दूसरे को 45 डिग्री पर काटती हैं।"

हाथी दांत का बना एक पैमाना भी मिला है (5 x 0.6 इंच)। उसमें 1.81 इंच को सत्ताइस हिस्सों में बांटा गया है। और इस प्रकार प्रत्येक भाग औसतन 0.0689 (0.67) इंच का है। ऐसे बीस भाग मोहंजोदड़ो में पाए गए शंख पैमाने पर अंकित दो वृत्तों के बीच की दूरी के लगभग बराबर हैं।

मोहंजोदड़ो पैमाना भी उल्लेखनीय है। पांच भागों के बीच की दूरी 1.32 इंच है जो लोथल पैमाने के बीस भागों की बीच की दूरी 1.338 (1.34) इंच के लगभग समान है। मोहंजोदड़ो पैमाने के दस भाग मिलकर 2.64 इंच के हैं, जो शायद सिंधु घाटी में मापने की बुनियादी इकाई रहा होगा। लोथल पैमाने के पहले दस भाग 0.689 इंच की दूरी दिखाते हैं - यानी करीब 0.7 इंच। बाद के समय की परंपरागत नाप ‘अंगुल' है जिसका उल्लेख कौटिल्य के अर्थशास्त्र में भी है। रोचक बात यह है कि यह नाप भी 0.7 इंच के बराबर ही है। इस प्रकार लोथल पैमाना मोहंजोदड़ो पैमाने

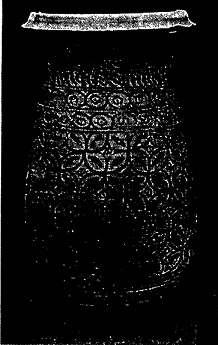
हड़प्पाकालीन एक मिट्टी का बर्तन जिस पर रेखागणितीय आकृतियों से नक्काशी की गई है।

भगवानपुरा से मिले चित्रित धूसर मृद भांड के कुछ टुकड़े। इन पर बनाए गए वृत या वृत के भीतर बनाई गई आकृतियों के बारे में ऐसा माना जाता है। कि इन्हें परकार जैसे किसी उपकरण से बनाया गया होगा।

कालीबंगा - मोहंजोदड़ो-हड़प्पा कालीन सभ्यता का एक नगर। आज से लगभग चार हजार साल पहले के इस शहर में सलीके से बने एक मकान का फर्श और दीवारें आज भी मौजूद हैं।

कालीबंगा--- में खुदाई के दौरान इस मकान के फर्श पर लगाई गई टाइल्स मिलीं। इनके पैटर्न को देखकर लगता है कि पहले टाइल्स को फर्श पर लगाया गया होगा और बाद में इन पर वृत बनाए गए होंगे। इन वृत्तों की सटीकता को देखते हुए यह माना जाता है कि इन्हें ज़रूर परकार जैसे किसी उपकरण से बनाया गया होगा।

की तुलना में परंपरागत भारतीय माप विज्ञान के कहीं ज्यादा नज़दीक है।'' यह भी संभव है कि लोथल में दूरी नापने के लिए दो प्रकार के माप उपयोग में लाए जाते थे - एक सील जैसी छोटी चीजों के लिए और दूसरा इमारतें नापने के लिए।

1934 की खुदाई में कई चित्रांकन मिले जिन्हें देखकर ई. जे. एच. मैके आश्चर्यचकित हुए क्योंकि इनको बनाने के लिए “वस्तुतः एक यंत्र का इस्तेमाल किया गया होगा।''20 कुछ चित्र आयताकार घेरे मे बने हुए हैं, कुछ वृत्त में और कुछ बिना किसी वृत्त के। इनमें लगातार कई चार पंखुडियों वाले डिज़ाइन बने हैं। इनकी सटीकता परकार और पैमाने के उपयोग के बिना संभव नहीं है। ये नमूने 2500 ई. पू. के हैं।

लोथल में निजी मकानों में मिट्टी की ईंटों के चबूतरे पाए गए हैं। चबूतरे योजना और नाप में आयताकार हैं। गोल गड्ढे भी हैं। "चाहे ये यज्ञ से संबंधित थे या नहीं''(जैसा कि एस. आर. राव का विश्वास था)', यह तथ्य साफ है कि वहां के लोग पूर्ण रूप से सही वृत्त और आयत की रेखागणितीय आकृतियों से परिचित थे।

ज्यादा महत्व की बात यह है कि इस सभ्यता के सभी शहरी-केन्द्रों में ईंटें मिली हैं। प्रसिद्ध पुरातत्वशास्त्री के. एस. दीक्षित का मत थाः

"मोहंजोदड़ो और हड़प्पा में मकान बनाने में इस्तेमाल की गई ईंट अच्छी तरह पकाई हुई हैं और उनके अनुपात भी बेहतरीन हैं। पक्की ईंट का सबसे प्रचलित आकार 11 इंच x 5.25 इंच या 5.5 इंच और मोटाई 2.25 इंच से 2.75 इंच है। किसी भी अन्य काल के भवन निर्माताओं की तुलना में हडप्पा के लोगों ने अत्यंत व्यावहारिक आकार का उपयोग किया। और यह उल्लेखनीय है कि ऐतिहासिक काल में ईंटों का विकास अशोक के समय की ईंटों से शुरू होता है जो सिंधु घाटी की ईंटों से दो गुनी लंबी और चौड़ी थीं। ईंट का आकार कुषाण, गुप्त और मध्यकाल में क्रमशः कम होने लगता है पर उन सब में लंबाई, चौड़ाई और मोटाई अनुपात 1:1/2:1/4 कभी नहीं रहा जो जुड़ाई को सर्वाधिक मज़बूती प्रदान करता है?"

सिर्फ दीक्षित ही नहीं अन्य पुरातत्ववेत्ता भी हड़प्पा संस्कृति की ईंटों के अनुपात की तारीफ करते हैं। जॉन मार्शल ने कहा हैः

"दीवारें मिट्टी के गारे से जुड़ी ठोस ईंटों से बनी हैं। उपयोग में लाई गई ईंटों का आकार 11 इंच x 5.5 इंच x 2.75 इंच है यानी कि लंबाई, चौड़ाई और मोटाई का अनुपात 4 : 2 : 1 आता है जो कि मजबूत जुड़ाई के लिए ज्यादा उपयुक्त है।''

दीक्षित एक और रोचक मत देते हैं:

"(ईटों का) आदर्श अनुपात पूरी तरह से भुला नहीं दिया गया था, यह इस बात से प्रकट होता है कि बाद का एक ग्रंथ (कश्यप संहिता) ईंटों के लिए 10 अंगुल लंबाई, 5 अंगुल चौड़ाई और 2.5 अंगुल मोटाई का अनुपात सुझाता है। लेकिन इसमें संदेह है कि ऐतिहासिक काल में राजगीरों ने कभी इसका पालन किया हो। जो भी हो यह स्पष्ट है कि सिंधु सभ्यता की पकी ईंट भारत में अतुलनीय है और रोमन काल के आगमन के पहले सुमेर, मिस्र और अन्य देशों में की गई कोशिशों से भी उसकी तुलना नहीं की जा सकती है।''

इस प्रकार रेखागणित के उद्भव के लिए दो बुनियादी तत्व - राजगीर के औज़ार और ईंट निर्माण - 2500 ई. पू. में भी भारत में विद्यमान थे।

सिंधु घाटी सभ्यता का खात्मा क्यों हुआ यह अभी भी विवाद का विषय बना हुआ है। बहुत-सी परिकल्पनाएं सुझाई गई हैं - हम अभी उनकी चर्चा नहीं करेंगे। परन्तु इतना ज़रूर है कि पुरातात्विक खोजों में एक किस्म की गिरावट दिखती है। हड़प्पा सभ्यता के अंतिम दौर में शहर उतने नियोजित ढंग से बनते नहीं दिखते, घर बनाने के लिए पुरानी ईंटें दोबारा इस्तेमाल की जा रही थीं। शहरी सभ्यता में गिरावट के साथ-साथ कारीगरी और कला का ज्ञान भी खत्म हो गया।

तथापि, काफी समय बीतने के बाद हमारे पास भारत में रेखागणित के पुनर्जन्म के लिखित अभिलेख मिलते हैं। वे हैं शुल्ब या शुल्व सूत्र, जिसका शाब्दिक अर्थ है 'रस्सी से संबंधित सूत्रों का संग्रह'। यह कृति 600 ई. पू. की है।

रामकृष्ण भट्टाचार्यः आनंद मोहन कॉलेज, कलकत्ता के अंग्रेजी विभाग में रीडर तथा कलकत्ता विश्वविद्यालय के स्नातकोत्तर अंग्रेज़ी अध्ययन पाठ्यक्रम में अतिथि लेक्चरर। विज्ञान लेखन में रुचि।
अनुवाद: सुरेश मिश्रः इतिहास के पूर्व प्राध्यापक। भोपाल में रहते हैं।