कई खेल और पहेलियां ऐसी भी हैं जो गणित की पाठ्यपुस्तक का हिस्सा तो नहीं होती लेकिन उन्हें हल करने में मजा आता है। ऐसी बहुत सी पहेलियों का गणित शिक्षण में भी इस्तेमाल किया जा सकता है।
गणित में पहेलियों का अपना महत्व है। पहेलियां विद्यार्थियों को हल खोजने के लिए प्रेरित करती हैं। पहेलियों के साथ एक और अच्छी बात है कि इन्हें सुलझाते समय विद्यार्थियों को हल का तरीका खुद ही खोजना पड़ता है।
पहेलियां हल करने से छात्रों में सोचने का कौशल तो विकसित होता ही है। गणित की कई ऐतिहासिक पहेलियां बहुत मशहूर हैं, इनके जरिए विद्यार्थियों को गणित के इतिहास से भी परिचित कराया जा सकता है।
अक्सर पाठ्य पुस्तकों में दिए सवालों का बच्चों के जीवन से कोई सरोकार नहीं होता है। समस्याओं का समाधान खोजने के दौरान छात्रों में उपयुक्त तरीके चुनने का कौशल भी विकसित होगा।
बुनियादी जोड़ और घटाना
गतिविधिः जादुई वर्ग (Magic Square)
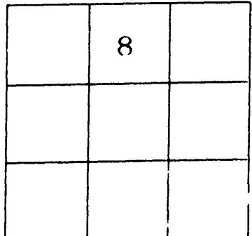
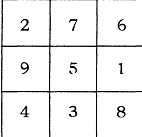
1,2,3,4,5,6,7,8,9 अंकों को सजाकर एक जादुई वर्ग बनाएं। इस जादुई वर्ग में हरेक खड़ी कतार व आड़ी कतार की संख्याओं का जोड़ भी 15 होगा। दोनों विकर्ण की संख्याओं का जोड़ भी 15 होगा। 15 को हम जादुई अंक कहेंगे।
-- 1 से 9 तक के अंकों को 3 x 3 के जादुई वर्ग में सजाने के कितने अलग-अलग तरीके हो सकते है
-- चित्र में दिखाए गए खाने में 8 के अंक को रखें और फिर हल खोजें?
--1 से 16 तक के अंकों को 4 x 4 के जादुई वर्ग में 880 तरीकों से सजाया जा सकता है।
अगर जादुई संख्या 34 हो तो आप इनमें से कितने तरीके खोज सकते हैं?
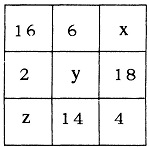
-- दाईं ओर बने जादुई वर्ग में (x, y, z) के मान क्या होंगे? (यहां जादुई संख्या 30 है।)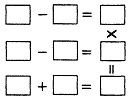 
जोड़-घटाना-गुणा-भाग चारों एक साथ
गतिविधिः खानों में अंक भरना
1 से 9 तक के अंकों को खानों में इस प्रकार भरें कि चारों समीकरण सही हों।
अब इन खानों में कुछ अन्य संख्याएं भरें जिससे चारों समीकरण सही बने रहें।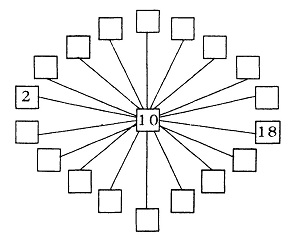 
गतिविधिः जोड़ का गोला
1 से 19 तक की संख्याओं को खानों में इस प्रकार भरें जिससे कि हरेक सीधी रेखा पर स्थित, तीनों अंकों का जोड़ 30 हो
उल्टी संक्रियाएं
-- जोड़, घटाने की उल्टी प्रक्रिया होती है और घटाना, जोड़ने की। इसी तरह गुणा और भाग भी एक-दूसरे के उल्टे होते हैं।
-- अगर आप कोई संक्रिया करें और फिर उसका उल्टा करें, तो
आपने जहां से शुरू किया था आप वहीं लौट आएंगे। उदाहरण के लिए 7+2-2= 7
अगर आप एक से अधिक संक्रियाएं कर रहे हैं, तो आपने जहां से शुरू किया, वहीं पर लौट आएंगे। उदाहरण के लिए: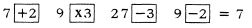
गतिविधिः
छात्रों को नीचे दिए निर्देश दीजिए।
-- मैं एक संख्या सोचता हूं। अगर मैं उसे 5 से गुणा करके उसमें से | 7 घटा दें तो उत्तर 58 आता है। मैंने कौन-सी संग्या सोची होगी?
-- मैं एक संख्या सोचता हूं। उसे 3 से गुणा करता हूं। फिर उसमें से 6 घटाता हूं। अंत में जब मैं उसे 2 से भाग देकर, उसमें 5 जोड़ता हूं तो उत्तर 23 आता है। मैंने कौन-सी संख्या सोची थी?
शुरू में सोची गई संख्या को खोजने के क्या तरीके हो सकते हैं? इस बारे में छात्र आपस में चर्चा करें।
कौशल और चतुराई के खेल
गतिविधि : नाईन मेन्स मॉरिस
यह खेल दो खिलाडियों के लिए है। मिस्र, श्रीलंका और नार्वे में भी इस खेल के बोर्ड पाए गए हैं।
नियम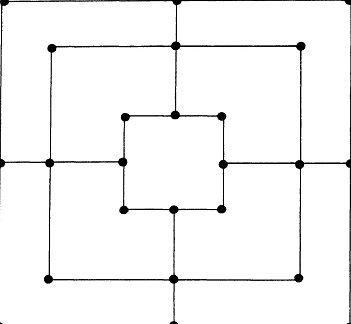 
1. खिलाड़ी बारी-बारी से बोर्ड की काली बिन्दियों पर एक-एक गोटी रखते हैं। इस प्रकार दोनों खिलाड़ी, अलग-अलग रंगों की नौ-नौ गोटियां बोर्ड पर रखेंगे।
इस खेल के बोर्ड को किसी कागज़, गत्ते, स्लेट या फर्श पर बनाकर गोटियों की मदद से अपने साथी के साथ मेल शुरू कीजिए।
2. खिलाड़ी बारी-बारी से बोर्ड पर एक गोटी को खाली बिन्दी पर चलाते हैं। गोटी को, एक रेखा में, किसी भी दिशा में चलाया जा सकता है परंतु जिस बिन्दी पर गोटी रखी हो उस पर से कूदना मना है।
3. जब कोई खिलाड़ी अपनी तीन गोटियां, एक-रेखा में ले आए तब वह दूसरे खिलाड़ी की एक गोटी को बोर्ड पर से हटा सकता है।
4. जिस खिलाड़ी की सिर्फ दो गोटियां ही बचें और वह चाल नहीं चल पाए तो वह हार जाता है।
इस खेल को कई बार खेलें और फिर निम्न प्रश्नों पर चर्चा करें
➔ क्या खेल शुरू करने की कोई सबसे अच्छी चाल है?
➔ दोनों खिलाडियों के एक-एक चाल चलने के बाद कुल कितनी स्थितियां संभव हैं?
➔ तीन गोटियों को एक-रेखा में लाए बिना बोर्ड पर अधिक-से-अधिक कितनी गोटियां रखी जा सकती हैं?
• एक चींटी बोर्ड पर कहीं से भी चलना शुरू करती है और सभी रेखाओं से होकर गुजरती है। उसके लिए सबसे छोटा रास्ता
कौन-सा होगा?
गाय और तेंदुआ
दो लोगों के लिए श्रीलंका से एक खेल।
नियम
➔ खिलाड़ी-1 के पास एक ही रंग के दो काउंटर होंगे। ये तेंदुए हैं।
➔ खिलाडी-2 के पास किसी अन्य रंग के 24 काउंटर होंगे। ये गायें
➔ खिलाड़ी-1 बोर्ड की किसी भी बिन्दी पर, कहीं भी एक तेंदुए को रख सकता है।
गाय और तेंदुए के खेल के लिए इस बोर्ड को किमी गत्ते पर या किसी फर्श पर या स्लेट पर बना लीजिए। अपने साथी के साथ गाय और तेंदुए का बंटवारा कर खेल की शुरुआत कर सकते हैं।
➔ उसके बाद खिलाड़ी-2 बोर्ड की किसी भी बिन्दी पर एक गाय को रख सकता है। -
➔ खिलाडी-1 फिर दूसरे तेंदुए को रखेगा और उसके बाद खिलाडी 2 दुसरी गाय को।
➔ गाय और तेंदुए हर चाल में, किसी भी रेखा और दिशा में केवल एक ही बिन्दी चला सकते हैं।
➔ खिलाड़ी-1 तेंदुए को हरेक चाल में केवल एक बिन्दी ही चला सकता है। खिलाडी-2 हरेक चाल में बोर्ड पर एक और गाय येगा। सभी 21 गायें रखने के बाद ही खिलाडी-2 अपनी गायों को चला सकेगा। वह हर चाल में एक बिन्दी ही चला सकेगा।
तेंदुआ किमी भी सीधी रेखा में गाय पर कूद सकता है और रिक्त स्थान पर जाकर गाय को मार सकता है। सामान्यतः बोर्ड पर सभी गायों के रखने में पहले ही तेंदुए गायों को मारना शुरू कर देते हैं। गायें, तेंदुओं को नहीं मार सकती हैं परन्तु वे तेंदुओं की घेराबंदी करके उन्हें फंसा सकती हैं और उन्हें चलने से रोक सकती हैं।
जीतने के लिए तेंदुओं को, सभी गायों को मारना होगा, या फिर गायों को तेंदुओं की घेराबंदी करके उनकी चाल पर पूरी तरह रोक लगानी होगी।