पी. बी. सुनील कुमार एवं अभिजीत देशपांडे
वैसे तो गैलीलियो का नाम कई प्रयोगों के साथ जुड़ा है। इस बार मामला ऊर्जा परिवर्तन का है। उन्होंने आसानी से मिलने वाली सामग्री से प्रयोग किए और निष्कर्ष निकाले। देखते हैं यह सब इतना सहज कैसे था।
यदि हम किसी नत समतल यानी ढलान के शीर्ष बिन्दु पर कोई वस्तु रखें तो वह नीचे की ओर आती है और इस प्रक्रिया में इसकी गति बढ़ती जाती है। गैलीलियो ने पहली बार सन् 1630 में यह बताया कि नीचे आने वाली वस्तु का वेग इसके किसलना प्रारंभ करने वाले बिन्दु की ऊंचाई पर निर्भर करता है, न कि समतले के झुकाव पर।
नीचे दिए गए चित्र को देखिए। यह हमें बताता है कि 'बी' तथा 'सी' बिन्दुओं पर लुढ़कने वाले पिंड की गति एक समान रहती है। अब हम इस प्रक्रिया में ऊर्जा में होने वाले परिवर्तन को देखेंगे।
जब पिंड नत समतल यानी ढलान के शीर्ष पर अचल रहता है तब इसमें कोई गतिज ऊर्जा नहीं होती क्योंकि इसका कोई वेग नहीं होता। शीर्ष बिन्दु पर ऊंचाई ‘एच' के कारण इसकी स्थितिज ऊर्जा अधिकतम होती है। (समीकरण mgh के अनुसार)। माना कि इस प्रक्रिया में ऊर्जा में किसी प्रकार का क्षय नहीं होता। (क्या आप सोच सकते हैं कि यहां पर ऊर्जा के क्षय के संभावित कारण क्या हो सकते हैं?)
जब वस्तु समतल के आधार पर होती है तब इसकी संपूर्ण स्थितिज ऊर्जा गतिज ऊर्जा में परिवर्तित हो जाती है। चूंकि दोनों चलन पथ के प्रारंभ में ऊर्जा की मात्रा समान थी तो अंत में भी उनमें समान ऊर्जा रहनी चाहिए। अर्थात् उनका वेग समान होना चाहिए। परन्तु इसे सिद्ध कैसे किया जा सकता है? गैलीलियो ने इसे सिद्ध करने के लिए एक प्रयोग किया जिसकी हम आगे चर्चा करेंगे।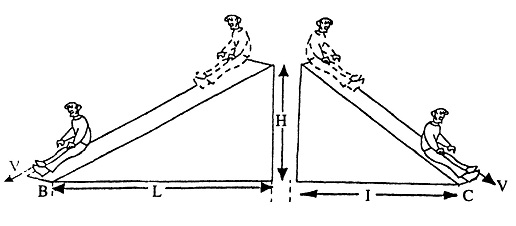
आप कहेंगे कि इसमें मुश्किल क्या है? इसे तो वेग नापकर सिद्ध किया जा सकता है। लेकिन इसे साधारण आधुनिक घड़ियों द्वारा जांचकर देखने पर आप पाएंगे कि यह इतना आसान नहीं है। अब ज़रा सोचिए कि गैलीलियो के काल में जलघड़ियों से यह कैसे संभव हो सकता था! इसलिए इसे सिद्ध करने के लिए गैलीलियो ने साधारण पेंडुलम यानी दोलक का उपयोग किया।
प्रयोग करने के लिए हमें निम्नलिखित सामग्री की आवश्यकता पड़ेगी - दो तीन-इंच लंबी कीलें, हथोड़ी, कुछेक मीटर मज़बूत धागा और हुक लगी हुई धातु की एक गेंद या दोलक या इस जैसा कोई भार।
कील को दीवार में लगभग एक इंच तक गाड़ दें। इसके बाद दोलक को धागे की सहायता से इस कील से लटका दें। ध्यान रहे कि यह दीवार को स्पर्श न करे।
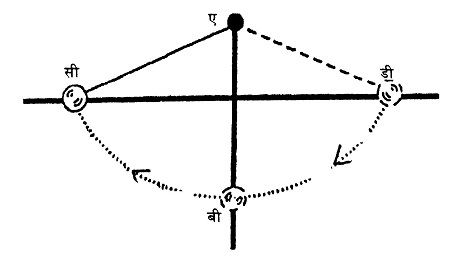
मान लें कि रुकी हुई अवस्था में कील की स्थिति 'ए' है और भार की स्थिति 'बी' है। इस प्रकार हमारे पास ‘एम' द्रव्यमान का एक पेंडुलम है जो ‘ए-बी' लंबाई से लटका हुआ है।
अब चित्र में दिखाए अनुसार दीवार पर एक रेखा ए-बी और इसके लंबवत एक रेखा सी-डी खींचते हैं। तत्पश्चात पेंडुलम की डोरी को तान कर रखते हुए भार को लंबवत रेखा पर 'डी' बिन्दु तक ले जाते हैं। यह स्पष्ट है कि दोनों रेखाओं ए-बी और ए-डी की लंबाई समान है।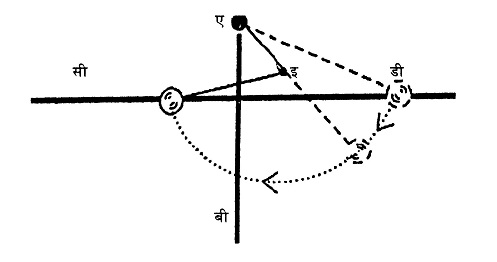
पेंडुलम को 'डी' बिन्दु तक ले जाकर छोड़ देते हैं। यह निम्नतम बिन्दु 'बी' से गुजरता हुआ दूसरी ओर क्षैतिज रेखा सी-डी के बिल्कुल करीब तक पहुंच जाता है और वापस ‘डी’ बिन्दु तक जाने लगता है। यदि हम प्रयोग निर्वात में करें तो यह दूसरी ओर क्षैतिज रेखा को छू लेगा। क्षैतिज । रेखा पर इस बिन्दु को हम 'सी' से चिन्हित कर देते हैं।
अब हम ऊपर दिए गए चित्र में दिखाए अनुसार 'ए' बिन्दु के नीचे और रेखा सी-डी के ऊपर 'ई' बिन्दु पर दुसरी कील गाड़ देते हैं। प्रयोग को दुबारा शुरू करने पर भार नीचे आता है और डोरी दूसरी कील से टकराती है। अब क्या होगा? भार दूसरी ओर आगे बढ़ता जाता है - इस तरह कि मानो अब यह 'ई' बिन्दु से लटका हुआ है! रोचक तथ्य यह है कि इस स्थिति में भी यह गोला रेखा सी-डी तक पहुंच जाता है।
अब दूसरी कील को थोड़ा और नीचे गाड़ देते हैं और प्रयोग को पुनः प्रारंभ करते हैं। यह देखने में आता है। कि जब तक डोरी के कील से टकराने पर दूसरी कील से भार तक की लंबाई कील से रेखा सी-ड़ी तक की लंबाई से अधिक है, तो इसी तरह के परिणाम मिलते हैं - यानी भार दूसरी कील पर दोलन करता हुआ सी-डी रेखा तक पहुंच जाता है।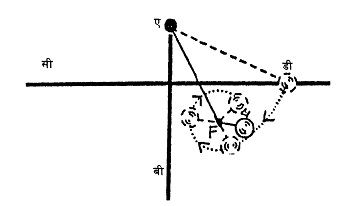 
अब आखिरी चित्र में दिखाए अनुसार दूसरी कील को रेखा सी-डी के इतना नीचे बिन्दु 'एफ' पर गाड़ देते हैं कि ऊपर वाली शर्त पूरी नहीं हो सकती। यानी इस बिन्दु से लटकने पर कील 'एफ' से भार तक की दूरी कील से रेखा सी-डी तक की दूरी से कम हो जाती है। इस प्रकार हम देख सकते हैं कि दूसरी कील से भार को लटकाने वाली डोरी की वर्तमान उपलब्ध लंबाई' इतनी नहीं है कि वह भार को रेखा सी-डी तक ले जा सके। ऐसे में क्या होगा? भार को पुनः दोलन कराने पर अब वह कील के चारों ओर डोरी को लपेट देता है! अब इसकी व्याख्या कैसे करें?
दरअसल हमने इस प्रयोग में जो देखा वह ऊर्जा के संरक्षण का प्रदर्शन और नतीजा है।
उपरोक्त वर्णित प्रयोग में अगर वायु के प्रतिरोध के कारण ऊर्जा का क्षय न हो, तो पेंडुलम के गिरने के दौरान, यानी इसके कील से टकराने तक इसके द्वारा हासिल की गई गतिज ऊर्जा इसे रेखा सी-डी तक वापस पहुंचाने के लिये पर्याप्त होती है। याद रखें कि दोलक में रेखा सीडी तक वापस पहुंचने के लिए हमेशा पर्याप्त ऊर्जा होती है।
यदि डोरी : छोटी हो तो भार कील के चारों घूम जाता है और यहां तक कि कील के ठीक उपर लम्बवत स्थिति पर भी पहुंच सकता है। इस स्थिति में भी इसमें कुछ गतिज ऊर्जा रहती है और यह आगे बढ़ते हुए कील के चारों ओर वृताकार गति करता है। (जब यह रेखा सी-डी तक पहुंचता है तभी इसकी समस्त गतिज ऊर्जा स्थितिज ऊर्जा में परिवर्तित होती है।) कक्षा में अपने साथियों के साथ भी इस प्रयोग को करके देखिए।
पी. बी. मुनील कुमार एवं अभिजीत देशपांडे का यह लेख जंतर-मंतर के जुलाई-अगस्त, 2002 अंक में प्रकाशित हुआ था।
अनुवादः निशांतः शौकिया अनुवादक, फ्रेंच भाषा सीख रहे हैं। फिलहाल भोपाल में रहते हैं।