ज़ीरो बनाम कट्टम

मोहम्मद उमर

कुछ बातें यूँ तो बहुत ही मामूली हुआ करती हैं, इतनी कि उस तरफ हमारा ध्यान भी बहुत कम जा पाता है। लेकिन यदि वे बार-बार हमारेे सामने आती जाएँ तो उनसे मुँह भी नहीं मोड़ा जा सकता। ऐसे में ज़रूरी हो जाता है कि सिलसिलेवार ढंग से उस पर बात की जाए। ऐसा ही एक मुद्दा है ‘ज़ीरो बनाम कट्टम’ का। यानी, गुणा के सवाल करते समय, दूसरी पंक्ति में गुणनफल लिखने से पहले ‘कट्टम लिखा जाना चाहिए या शून्य’?

शिक्षक प्रशिक्षणों के दौरान गुणा के सवालों पर बात शुरू करते ही कोई-न-कोई शिक्षक ज़रूर इस बहस को छेड़ देता है। बस फिर क्या, पूरी की पूरी कक्षा के सहभागी दो गुटों में बँट जाते हैं। एक गुट पुरज़ोर तरीके से कट्टम की वकालत करता है जबकि दूसरा गुट ज़ीरो रखे जाने की सिफारिश। दोनों ही गुट के लोग अपने-अपने तर्क देते हैं और अपने तरीके को न सिर्फ सही ठहराते हैं, बल्कि दूसरे के तरीके को सिरे से खारिज भी करते हैं।

आइए, इस पर आगे बात करने से पहले यह समझने का प्रयास करते हैं कि आखिर माजरा क्या है।
इसके लिए एक बहुत ही सरल-सा गुणा का सवाल ले लेते हैं:
7 x 8 = 56
हम सभी जानते हैं कि यहाँ पर दिख रहा कट्टम का निशान ‘गुणा’ करने का इशारा देने वाला निशान है। अब हम ऊपर तस्वीर में दिखाया गया सवाल जाँचते हैं। इस सवाल में दो कट्टम दिख रहे हैं। पहला वाला बेशक ‘गुणा’ करने का निशान है, जबकि दूसरा कट्टम दिखता तो पहले जैसा ही है लेकिन वह गुणा का निशान नहीं है। तो फिर वह क्या है? और इसे यहाँ पर क्यों लगाया जा रहा है? इस निशान का यहाँ लगाया जाना सही है या गलत?

‘ज़ीरो’ या शून्य के पक्षधर
आइए पहले उन लोगों की कुछ आपत्तियों को समझ लेते हैं, जो इस कट्टम के स्थान पर ‘ज़ीरो’ या शून्य रखने की वकालत करते हैं।
1. एक ही सवाल में एक जैसे निशान दो से ज़्यादा बार आते हैं और उनके मायने अलग-अलग होते हैं जो समस्या पैदा करते हैं।
2. अलग-अलग संख्याओं से प्राप्त गुणनफल को नीचे लिखने के बाद जोड़ किया जाता है। यहाँ 411 में 274 x को जोड़ा जा रहा है। संख्याओं के परम्परागत परिचित ढाँचे के अनुरूप 411 में 274 x को जोड़ने की बात करना कहीं अधिक पेचीदा है। इसकी बजाय 411 में 2740 को जोड़ना ज़्यादा सहज है।
3. 137 को 23 से गुणा करने की प्रक्रिया में हम गुणा के वितरण नियम का पालन कर रहे होते हैं, यानी कि

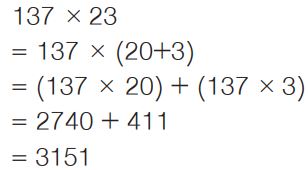
तो, कट्टम के स्थान पर ‘ज़ीरो’ लिखकर हम विधि के प्रयोग में भी इसी सैद्धान्तिक प्रक्रिया का पालन कर रहे होंगे।
4. बच्चों के लिए, जिन्होंने अभी जोड़ करने की विधि को भी ठीक ढंग से आत्मसात नहीं किया है उन्हें हम ऐसी दो संख्याओं का जोड़ करने को कह रहे हैं, जिनमें से एक में कट्टम जैसा निशान है। यह उनकी मुश्किल को और भी बढ़ा देता है। अब ऐसे में 411 और 274 x को जोड़ने के दौरान यदि वे 685 लिख बैठें तो उनका क्या दोष?
इस तरह के और भी कई तर्क निकल कर आते हैं, जो पुरज़ोर तरीके से यह सिफारिश करते हैं कि कट्टम की जगह ज़ीरो का इस्तेमाल किया जाना चाहिए।

कट्टम के पक्षधर
अब दूसरे खेमे के लोगों की बात भी कर ली जाए। हालाँकि इस खेमे में ऐसे बहुत ही कम लोग मिलते हैं जो अपनी बात को मज़बूती से रख सकें। ज़्यादातर तो परम्परावादी किस्म के ही मिलते हैं, जिनका अटूट विश्वास होता है कि जिस तरह हमें सिखाया गया, वैसे ही हम बच्चों को सिखा रहे हैं। कट्टम ही क्यों लगाया जाना चाहिए, इसपर कोई बहुत ठोस तर्क प्रस्तुत नहीं होता। बस, रिवाज़ को बनाए रखने और कोई बड़ी दिक्कत महसूस नहीं करने का भाव ही प्रमुख होता है। इनके तर्क प्रमुखत: इस प्रकार के होते हैं।
1. हमारे गुरूजी ने जैसे सिखाया था, वैसे ही हम भी सिखा रहे हैं। हम-आप सीख गए हैं तो बच्चे भी गुणा करना सीख ही जाएँगे।
2. उत्तर तो सही आ रहा है न, कैसे भी जाँच लो यही उत्तर आएगा।
3. यह जगह खाली छोड़ना है, बिना कुछ लिखे छोड़ देंगे तो बच्चे गलती से वहाँ पर संख्या लिख देंगे। उनका पूरा सवाल ही गलत हो जाएगा। कट्टम का निशान लगाने से जोड़ करने में गलती नहीं होती है।

गणित को लेकर मेरी जो समझ है उसके मुताबिक मैं कतई इस पक्ष में नहीं हूँ कि हमें इन दो मत वाले खेमों में से किसी एक की तरफ झुक जाना चाहिए। हाँ, लेकिन यह बात ज़रूर है कि बच्चों के लिए कब, क्या बेहतर होगा इस बात का ध्यान रखते हुए आगे बढ़ना चाहिए। इसके लिए सबसे पहली ज़रूरी शर्त तो यही हुई कि हम खुद क्या कर रहे हैं और क्यों कर रहे हैं, इसे बेहतर तरीके से समझ सकें। ‘ज़ीरो’ और ‘कट्टम’ का प्रयोग करने पर मेरा जो नज़रिया है उसे मैं विस्तार से रखना चाहता हूँ।

ज़ीरो का प्रयोग
मान लेते हैं कि हमें 137 को 23 से गुणा करना है। स्थानीय-मान की अवधारणा के अनुसार 137 को देखा जाए तो यह 7 इकाइयाँ, 3 दहाइयाँ और 1 सैकड़ा का संयोजन है और हमारी मान्यता है कि किसी भी संख्या को लिखते समय हम दाईं से बाईं तरफ बढ़ते हुए इसका पालन करेंगे। ऐसा ही 23 के लिए भी है कि इसमें 3 इकाइयाँ और 2 दहाइयाँ हैं।
अब आगे जब हम 137 में 23 का गुणा करेंगे तो प्राप्त गुणनफल को भी हमें इसी स्थानीयमान की अवधारणा और अपनी इन्हीं मान्यताओं के अनुरूप रखना होगा। संख्याओं में निहित मात्रा और गुणा करने की समझ को आधार बनाकर हम यह अन्दाज़ा लगा सकते हैं कि 137 में 23 का गुणा करने पर गुणनफल कितना मिलेगा।
137 x 20 = 2740
137 x 30 = 4110
तो, 137 x 23 का मान 2740 से कुछ ज़्यादा होगा, लेकिन 4110 से तो ज़रूर काफी कम ही होगा।
विधि का इस्तेमाल ज़रूरी है, लेकिन कई बार यह हमें गणित की आम समझ से भी महरूम कर देती है। जिन मानक विधियों का आज हम बहुतायत में प्रयोग कर रहे हैं वह समस्या-समाधान के विभिन्न तरीकों में से ही एक तरीका है, लेकिन हमने विधि सिखाने को ही गणित मान लिया है। कक्षाओं में सिखाई जा रही तमाम मानक विधियाँ ‘अन्तिम परिष्कृत स्वरूप’ हैं, जिनके सही इस्तेमाल से हम जल्दी सटीक उत्तर तक पहुँच सकते हैं। जल्दी से सही उत्तर पाने की यही लालसा अवधारणा की समग्र समझ और विधि के पीछे काम कर रहे सिद्धान्त तक पहुँचने में बाधक होती है। अब जैसे इसी सवाल को बारीकी से देखते हैं।

हम अपने बच्चों को क्या सिखाते हैं? 3 से क्रमश: 7, 3 और 1 को गुणा करते जाओ और नीचे लिखते जाओ। अब नीचे जाकर इकाई के स्थान पर कट्टम लगा दो और इसी तरह एक बार फिर 2 से क्रमश: 7, 3 और 1 को गुणा करके लिखते जाओ। इस प्रक्रिया में बस हासिल का सही प्रयोग और संख्याओं को उनके सही स्थान पर लिखते जाना है। लेकिन, एक महत्वपूर्ण बात छूट रही है। 137 को तो ‘एक सौ सैंतीस’ के रूप में देखा ही नहीं गया और न ही 23 को ‘तेईस’ के रूप में देखा गया। विधि का प्रयोग करके हमने 3 का गुणा 7, 3 और 1 में तथा 2 का गुणा 7, 3 और 1 में कर दिया है। इस तरह हमें अन्दाज़ लगाने की थोड़ी-सी ज़हमत भी नहीं उठानी पड़ी, न ही ठहरकर यह सोचने की ज़रूरत पड़ी कि किस संख्या में हम किस संख्या का गुणा करने जा रहे हैं। हाँ, इसके बावजूद हमारा उत्तर सही हो जाने की प्रबल सम्भावना है, बशर्ते विधि के नियमों का उल्लंघन कहीं पर भी न किया गया हो। यही हो रहा है हमारी कक्षाओं में भी।
आइए पहले इसे समझ लेते हैं कि यह कट्टम क्यों लगा रहे हैं।

स्थानीय मान के अनुरूप हम ‘137’ को कुछ समूहों या बण्डलों के रूप में देख रहे हैं। दस आधारित संख्या पद्धति हमें सिर्फ नौ खुली वस्तुएँ रख सकने की इजाज़त देती है। चीज़ों के दस होते ही उन्हें एक नए बण्डल के रूप में देखना होगा। इस तरह 137 में 7 खुली इकाइयाँ हैं, ऐसी 30 खुली इकाइयों से बनी हुई 3 दहाइयाँ हैं और ऐसी ही 10 दहाइयों से मिलकर बना हुआ 1 सैकड़ा है। इसी तरह 23 भी 3 खुली इकाइयों और 2 दहाइयों से मिलकर बना है। अपनी इसी समझ को हम गुणा करने के दौरान इस्तेमाल करने वाले हैं।

कट्टम की परम्परा
सबसे पहले हम प्राप्त होने वाले बण्डलों के लिए स्थान निर्धारित कर रहे हैं। इकाई, दहाई, सैकड़ा और हज़ार...यदि ज़रूरत पड़े तो इसके आगे भी। हमें खयाल रखना होगा कि कोई भी संख्या हो या किन्हीं दो संख्याओं का गुणनफल, उसे स्थानीय-मान और संख्याओं के निर्धारित स्थानों के अनुरूप ही रखना होगा। इसे आगे भी याद रखेंगे, क्योंकि यही वह बात होगी जिसका पालन करते हुए हम या तो ‘कट्टम’ की तरफ बढ़ रहे होंगे या फिर ‘ज़ीरो’ की तरफ।

चित्र में दिए गए हल में देख सकते हैं कि सवाल के ऊपर लिखे इकाई, दहाई और सैकड़ा ने संख्याओं के स्थान निर्धारित कर दिए हैं। आप देख सकते हैं कि 137, 23, 411 और 3151 इसका अनुपालन कर रहे हैं। यूँ तो 274 x भी इस नियम की अनुपालना कर रहा है, लेकिन इस पर और बात करने की ज़रूरत है, ताकि हम समझ सकें कि कट्टम की ज़रूरत क्यों पड़ रही है।
सवाल में प्रदर्शित दोनों कट्टम के निशान एक जैसे दिखते ज़रूर हैं, पर पहला वाला - जो कि 23 के आगे लिखा है - गुणा का निशान है। यह 137 में 23 का गुणा किए जाने का संकेत है।

दूसरा निशान, जो कि नीचे लगा हुआ है, वह भी कट्टम ही है परन्तु यह क्या अभिव्यक्त कर रहा है, इसे समझने के लिए गुणा के इस सवाल को हल करते हुए आगे बढ़ते हैं।
137 का गुणा 23 से करना है। हम जानते हैं कि 20 और 3 का योग 23 होता है। अत: यदि 137 को 3 और 20 से अलग-अलग गुणा करने से प्राप्त होने वाले गुणनफलों को जोड़ दें तो अपेक्षित परिणाम प्राप्त हो जाएगा। ऊपर, हमने देखा है कि कट्टम के स्थान पर ‘ज़ीरो’ रखा जा रहा है। यहाँ भी असल में 137 को पहले 3 से और फिर 20 से गुणा किया जा रहा है। अन्तत: दोनों परिणामों का योगफल किया जा रहा है। इस पूरी प्रक्रिया में प्रत्येक संख्या या प्राप्त हो रहे परिणामों के सभी अंकों को स्थानीय मान के अनुरूप जमाया जा रहा है। ह सै द इ
1 37 x 23
4 1 1 -- 137 में 3 का गुणा करने से प्राप्त परिणाम
2 7 4 0 -- 137 में 20 का गुणा करने से प्राप्त परिणाम
3 1 5 1 -- ऊपर प्राप्त दोनों परिणामों का योगफल

गुणा की प्रक्रिया
अब जानने का प्रयास करते हैं कि ज़ीरो के स्थान पर कट्टम रखे जाने के क्या मायने हैं। यहाँ हम गुणा की प्रक्रिया और उसमें स्थानीयमान की महत्वपूर्ण भूमिका को भी साथ ही साथ समझते चलेंगे।
ह सै द इ

    1 3 7
    x 2 3   
    4 1 1
  2 7 4 x   
 3 1 5 1

यहाँ पर भी 137 में 23 का ही गुणा किया जाना है। फर्क सिर्फ इतना है कि अब हमें 23 को 20 और 3 के रूप में न देखकर 2 दहाइयों और 3 इकाइयों के रूप में देखना होगा। अपने समझने के लिए हम यह मान लेते हैं कि किसी संख्या को इकाई से गुणा किए जाने पर हमें इकाइयाँ ही प्राप्त होंगी, लेकिन क्योंकि संख्या लिखने का ढाँचा ही दस आधारित स्थानीयमान के नियम (कोई भी चीज़ नौ होने तक ही खुली रह सकती है, दस होते ही उसे एक बण्डल/समूह में रखा जाना होगा) से बँधा हुआ है, अत: गुणा करने के फलस्वरूप प्राप्त परिणाम लिखते समय भी स्थानीय-मान के नियमों का पालन किया जाना अनिवार्य है।

तो, एक सौ सैंतीस को तीन इकाइयों से गुणा करने पर हमें कुल ‘चार सौ ग्यारह’ इकाइयाँ प्राप्त हो रही हैं जिसे संख्याओं के रूप में रखने से 411 यानी 4 सैकड़ा, 1 दहाई और 1 इकाई मिल जाती है। अपनी विधि को देखकर गौर करें तो हम पाएँगे कि 411 के तीनों ही अंकों को कहाँ रखा जाना है इसका निर्णय हम 411 प्राप्त कर लेने के बाद नहीं करते हैं, बल्कि अंकों के लिए स्थान निर्धारण 137 के 3 से गुणा करने की प्रक्रिया में स्वत: ही होता जाता है।

हम सबसे पहले 137 के 7 को 3 से गुणा करते हैं। इस तरह सात इकाइयाँ तीन गुना होकर इक्कीस इकाइयाँ बना देती हैं। इन इक्कीस इकाइयोंे से 2 दहाइयाँ और 1 इकाई प्राप्त होती है। दहाइयाँ, यानी जिसके अन्दर दस इकाइयाँ हैं। तो, इस 1 इकाई को तो हम नीचे दर्ज़ कर देते हैं लेकिन 2 दहाइयों को हम अभी इसलिए दर्ज़ नहीं करते क्योंकि कुछ और दहाइयाँ प्राप्त होने की सम्भावना है। अत: दहाइयों का हिसाब अगले चरण में लगाया जाएगा।
अब अगले चरण में तीन दहाइयों का तीन गुना करने से हम 9 दहाइयाँ प्राप्त कर लेंगे। जब हम सभी दहाइयों का हिसाब करते हैं तो अभी की 9 और पहले ही प्राप्त हो चुकी 2 दहाइयों को मिला लेने से कुल 11 दहाइयाँ बन जाती हैं। दस आधारित स्थानीयमान का नियम कहता है कि चीज़ों के दस होते ही एक समूह/बण्डल बना लेना है। अत: 10 दहाइयों को मिलाकर एक समूह/बण्डल बना लेंगे, जो कि सैकड़ा - जिसमें सौ इकाइयाँ हैं - कहलाएगा। इस तरह हमें 1 दहाई और 1 सैकड़ा प्राप्त हो गया है। तो अब नीचे हम सिर्फ 1 दहाई को ही दर्ज़ कर सकते हैं। सैकड़ा का हिसाब आगे करेंगे क्योंकि और भी सैकड़ा प्राप्त होने की सम्भावना है।

अगले चरण में 1 सैकड़ा को 3 गुना करने से हमें तीन सैकड़ा प्राप्त होंगे। ये तीन सैकड़ा और पहले से प्राप्त एक सैकड़ा मिलकर कुल चार सैकड़ा बना देंगे। इसे दर्शाने के लिए हमें नीचे, सैकड़ा के कॉलम में सिर्फ 4 लिखने की ज़रूरत है।
तो हमने देखा कि किस तरह दाएँ से बाईं तरफ बढ़ते हुए हम क्रमश: इकाइयों, दहाइयों और सैकड़ा को तीन गुना करते रहे और प्राप्त इकाइयों, दहाइयों या सैकड़ा को उपयुक्त कॉलमों में रखते हुए उनका सही-सही लेखा-जोखा भी रखते गए। इस तरह हमेंे न सिर्फ 411 प्राप्त हो गया बल्कि उसके सभी अंक भी स्थानीय मान के अनुरूप निर्धारित स्थान पर ही रखे हुए मिले।

स्थानीयमान और कट्टम
और आगे बढ़ें इससे पहले एक खेल, खेल लेते हैं।
किसी 1 चीज़ को 10 गुना करते हैं। दस इकाइयाँ मिलीं जिसे हम 1 दहाई कह सकते हैं।
अब 2 चीज़ को 10 गुना करते हैं। बीस इकाइयाँ मिलीं, जिसे हम 2 दहाई कह सकते हैं।
और यदि 2 चीज़ों को 20 गुना करें तो चालीस इकाइयाँ मिलेंगी, जिसे हम 4 दहाइयाँ कह सकते हैं।

इसी तरह यदि 137 को 20 गुना करें तो दो सौ चौहत्तर दहाइयाँ मिलेंगी, जिसे हम कुछ दहाइयाँ, सैकड़ा और हज़ार में बदल सकते हैं।
इस अनुभव से हम पक्के तौर पर यह नतीजा निकाल सकते हैं कि कुछ चीज़ों को दस, बीस या तीस गुना करने पर हमें दहाई या दहाई से बड़ा जैसे, सैकड़ा, हज़ार या आगे भी लाख, करोड़ जैसी चीज़ें मिलने की सम्भावना तो है, पर समूह बन जाने के बाद कुछ भी खुली इकाइयों के रूप में नहीं बचने वाला। हम यूँ भी कह सकते हैं कि इस तरह अब हमें एक भी खुली इकाई मिल पाने की कोई सम्भावना ही नहीं बचती है। तो, जब हमें इकाइयाँ मिलना ही नही हैं तो अभी के लिए उनको दर्ज़ करने के स्थान पर हम कट्टम का निशान लगा सकते हैं। इस कट्टम के मायने ये होंगे कि ‘यहाँ पर एक भी इकाई आएगी ही नहीं।’

तो वापिस चलते हैं अपने सवाल पर, जहाँ हमें 137 को 20 गुना करना है। यह गुना करने से हमें जो भी मात्रा प्राप्त होगी उसे स्थानीय-मान के अनुरूप रखने पर हमें दहाई या फिर उससे बड़े समूह ही प्राप्त होंगे। अत: इकाई के कॉलम में एक भी इकाई नहीं आने वाली है। इसीलिए कट्टम लगाकर हम उस दरवाज़े को ही बन्द कर देते हैं।
अब जब हम 137 - जो कि 7 इकाइयाँ, 3 दहाइयाँ, और 1 सैकड़ा के रूप में है -- को 20 यानी 2 दहाइयों से गुणा करते हैं, तो उसकी प्रक्रिया क्या होती है?
हम सबसे पहले 7 इकाइयों को 2 दहाई से गुणा करते हैं। इस तरह चौदह दहाइयाँ मिल जाती हैं, जिनमें से 10 दहाइयों से एक सैकड़ा बनाकर हम उसे आगे किए जाने वाले सैकड़ा के हिसाब के लिए अलग रख लेते हैं जबकि बाकी बची रह गई 4 दहाइयों को नीचे दहाई के कॉलम में दर्ज़ कर लेते हैं।

अगले चरण में हम 3 दहाइयों को 2 दहाई से गुणा कर रहे हैं। इस तरह हमें 6 सैकड़ा प्राप्त होते हैं। ये 6 सैकड़ा और पहले का 1 सैकड़ा मिलकर कुल 7 सैकड़ा बनाते हैं। तो इस तरह हम नीचे सैकड़ा के कॉलम में 7 दर्ज़ कर लेते हैं।
अब अगले चरण में 1 सैकड़ा को 2 दहाई से गुणा किया जा रहा है। 1 सैकड़ा को 1 दहाई से गुणा करने पर दस सैकड़ा यानी 1 हज़ार मिलता है। इसी तरह 1 सैकड़ा को 2 दहाई से गुणा करने पर 2 हज़ार मिलता है। इसे दर्ज़ करने के लिए हम हज़ार के कॉलम में 2 लिख देते हैं। अब अन्त में बस दोनों परिणामों का जोड़ कर देना होता है।

   4 1 1
2 7 4 x
3 1 5 1

इस तरह ऊपरी तौर पर देखने पर हमें लगता है कि अपनी विधि का प्रयोग करते हुए हमने 137 को पहले 3 से और फिर 2 से ही गुणा किया है। हालाँकि यह 2 असल में 20 है, जिसे स्थानीयमान के नियम से प्राप्त सहूलियत के चलते हम 2 दहाई मान कर चल रहे हैं। यही 2 दहाइयाँ जब 137 से गुणा हो रही हैं तो परिणाम भी दहाइयों में परिवर्तित होकर ही मिल रहा है। इकाइयाँ कुछ भी नहीं मिल रही हैं और न ही उनके प्राप्त होने की कोई सम्भावना है।

हम कह सकते हैं कि 137 को 2 दहाइयों से गुणा करने पर हमें 274 दहाइयाँ मिल रही हैं। इकाइयाँ तो मिल ही नहीं रही हैं, एक भी नहीं। तो इकाई को दर्ज़ करने के स्थान को खाली भी छोड़ा जा सकता था, लेकिन इस स्थिति में अंकों की सीध थोड़ी भी गड़बड़ाने पर योगफल में गलती की सम्भावना बढ़ जाती है। खास तौर से छोटे बच्चे जो अभी अंकों को स्थानीय-मान के अनुरूप लिख पाने में थोड़ा कच्चे हैं, उनसे कई जगह गलतियाँ होने की सम्भावना और भी बढ़ जाती है। यह कट्टम हम सबको इस तरफ आने से रोकता है।

इस सारी चर्चा में हमने देखा कि ‘ज़्ाीरो’ रखना या ‘कट्टम’ लगाना तकरीबन एक ही बात है। सैद्धान्तिक तौर पर कोई बहुत बड़ा अन्तर नहीं है। दोनों ही तरीके गुणा करने के आधारभूत नियम का पालन करते हुए ही आगे बढ़ रहे हैं। हाँ, लेकिन शिक्षणशास्त्रीय नज़रिए से दोनों में कुछ अन्तर ज़रूर है। यदि हम खुद इस अन्तर को समझ रहे हैं और अपनी कक्षा के बच्चों को भी सवाल हल करने के दौरान ही इन सब बातों से अवगत करा रहे हैं तो कोई दिक्कत नहीं है, लेकिन यदि हम सिर्फ रिवाज़ बनाए रखते हुए ‘कट्टम’ या ‘ज़ीरो’ को रखते रहने की वकालत कर रहे हैं तो यह गणित शिक्षण के लिहाज़ से ठीक नहीं है। तो अन्तत: हम कह सकते हैं कि ‘ज़ीरो’ और ‘कट्टम’ के दरम्यान ‘बनाम’ जैसी कोई बात थी ही नहीं।

मोहम्मद उमर: अज़ीम प्रेमजी फाउंडेशन, चित्तौड़गढ़ में कार्यरत।