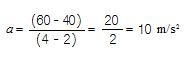दर की दर गति के ग्राफ और लाइनें

विवेक मेहता

अब तक हमने गति के सिर्फ उन मामलों पर ही बात की है जिनमें वस्तु का वेग एकरूप है। ऐसी गतियों में न केवल वस्तु की चाल बल्कि चाल की दिशा भी समय के साथ नहीं बदलती। लेकिन हमारे आसपास की अमूमन सभी गतियाँ इस श्रेणी में नहीं आतीं। आम गतियों में चाल, चाल की दिशा या दोनों ही समय के साथ बदलते रहते हैं। आप याद कर लीजिए किसी ट्रेन या बस के सफर को जो आपने कभी किया हो। बस या ट्रेन अपनी यात्रा कभी एक दिशा में तो कभी दूसरी, कभी तेज़ तो कभी धीमे, तो कभी रुकते हुए पूरी करती हैं; यानी कि उनका वेग सफर के दौरान एकरूप नहीं रहता, उसमें परिवर्तन आता रहता है।

जब भी कहीं परिवर्तन की बात आती है तो स्वभाविक है उस परिवर्तन की दर पर भी बात हो। और यहाँ बात हो रही है समय के साथ वेग में होने वाले परिवर्तन की। अब आप शायद सोच रहे हों कि वेग जो स्वयं ही एक दर है - समय के साथ वस्तु की स्थिति (दूरी) परिवर्तन की दर, क्या उसकी भी कोई दर होगी? तो जवाब है - हाँ। ऐसी कोई भी राशि जिसका मान स्थाई न होकर परिवर्तनीय हो तो हम उसकी दर की बात कर सकते हैं। रोज़मर्रा की गतियों में वस्तु के वेग में समय के साथ परिवर्तन होता रहता है इसलिए हम वेग परिवर्तन की दर की बात कर सकते हैं - एक दर की दर की बात।
वेग परिवर्तन की दर को एक नाम भी  दे  दिया  है  -  ‘त्वरण’ (Æacceleration)। एकरूप वेग के मामलों में चूँकि चाल व चाल की दिशा, दोनों में ही समय के साथ परिवर्तन नहीं होता, इसलिए इन मामलों में वेग परिवर्तन की दर, त्वरण शून्य होगा। वहीं ऐसी किसी भी गति या मामले में जिसमें चाल या चाल की दिशा या फिर दोनों में ही समय के साथ परिवर्तन हो, उसमें त्वरण शून्य नहीं होगा। गुणात्मक रूप से देखें तो वेग परिवर्तन के तीन रूप हो सकते हैं:

* वस्तु की चाल में परिवर्तन, लेकिन चाल की दिशा में नहीं
* चाल की दिशा में परिवर्तन, लेकिन चाल में नहीं
* दोनों में परिवर्तन।
इस लेख में हम पहले मामले यानी कि एक सीधे पथ के सबसे सरल स्वरूप तक ही सीमित रहेंगे। हम इस सीधे पथ पर वस्तु की चाल में होने वाले परिवर्तन के सबसे सरल स्वरूप को वेग-समय ग्राफ व उसकी लाइनों को आधार बनाकर देखेंगे। तो आइए चलें, दर-दर भटकने।

वेग-समय ग्राफ
ढलान के हिसाब से देखें तो किसी भी ग्राफ पर सन्दर्भ अक्षों के सापेक्ष तीन तरह की लाइनें हो सकती हैं -
* लाइनें जिनकी ढलान धनात्मक हो,
* लाइनें जिनकी ढलान ऋणात्मक हो,
* लाइनें जिनकी ढलान शून्य हो।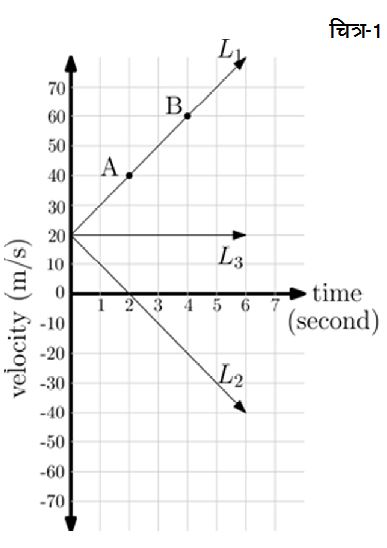

यही बात वेग-समय ग्राफ पर भी लागू होगी। इन तीनों तरह की लाइनों को चित्र-1 में दर्शाया गया है। ग्राफ पर अक्ष- x पर समय व अक्ष-y पर वेग को लिया गया है। साथ ही समय के लिए सेकण्ड की इकाई व वेग के लिए मीटर प्रति सेकण्ड (m/s) की इकाई ली गई है। ध्यान रहे कि हम एक सीधे पथ की गतियों की बात कर रहे हैं। एक सीधे पथ वस्तु के पास बढ़ने की दो दिशाएँ होती हैं: या तो आगे या पीछे1। अगर हम आगे बढ़ने की दिशा को धनात्मक व पीछे की दिशा को ऋणात्मक मानें तो इन दिशाओं में वस्तु के वेग को क्रमश: धनात्मक व ऋणात्मक मान सकते हैं। वेग के अक्ष पर धनात्मक व ऋणात्मक संख्याएँ यही दर्शा रही हैं। ‘लाइनों का नामकरण’ लेख में हमने देखा था कि किसी ग्राफ में खींची लाइनें ग्राफ के अक्षों को दर्शाती चर-राशियों x व y के बीच के सबसे सरल सम्बन्ध को दर्शाती हैं। इस सरल रेखीय सम्बन्ध को लाइन की ढलान ‘m’ व y-अन्त:-खण्ड ‘c’ के लिए समीकरण (1) से दर्शा सकते हैं:
y = mx + c                    (1)
इस सम्बन्ध के मुताबिक एक वेग-समय ग्राफ की अक्ष की लाइन जिसकी ढलान व y-अन्त:-खण्ड को क्रमश: ‘a’ व ‘u’ मान लें तो वेग (‘v’) व समय (‘t’) सरल रेखीय सम्बन्ध होगा:
v = at + u                    (2)
अब एक-एक करके इन तीनों लाइनों के द्वारा दर्शाई गई गतियों को लेते हैं व समीकरण (2) को समझने की कोशिश करते हैं।
(1) लाइन L1: चलिए झट से इस लाइन की y-अन्त:-खण्ड व ढलान2  निकाल लेते हैं। इस लाइन के लिए y-अन्त:-खण्ड होगा 20। लेकिन बस यह बतला देना तो काफी न होगा। यह 20 की संख्या क्या दर्शा रही है ये भी बतलाना होगा और उसके लिए सबसे आसान तरीका है कि इस संख्या को इसकी इकाई के साथ बतलाया जाए जोकि है m/s. तो इस तरह लाइन L1 के लिए y-अन्त:-खण्ड होगा  u = 20 m/s. यानी कि जिस क्षण से हमने वस्तु की गति का अध्ययन शुरू किया उस क्षण वस्तु का वेग 20 m/s था। जिसके मायने हुए कि समय t = 0 सेकण्ड पर वस्तु 20 m/sकी रफ्तार से आगे की ओर बढ़ रही थी। इस शुरुआती क्षण के बाद वस्तु के इस वेग में क्या परिवर्तन हुआ यह वेग-समय ग्राफ की ढलान पर निर्भर करेगा। L1 की ढलान इस लाइन पर किसी भी दो बिन्दुओं को लेकर निकाल सकते हैं। अगर इस दर को a से दर्शाएँ व लाइन L1 पर दो बिन्दु A(2, 40) व B(4, 60) लें तो लाइन की ढलान होगी:

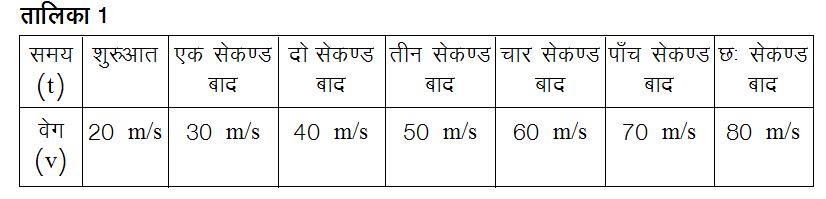
अब सवाल यह उठता है कि इस ढलान a = 10 m/s2 का मतलब क्या हुआ? ध्यान दीजिए इस ढलान की इकाई है m/s2 या फिर (m/s/s), या फिर (m/s) प्रति सेकण्ड। जैसा कि साफ है यह इकाई वेग प्रति समय की है। हमने पहले ही बात की कि वेग परिवर्तन की दर त्वरण कहलाती है। एक वेग-समय ग्राफ की ढलान समय के साथ वेग में आए इसी परिवर्तन की दर को दर्शाती है, यानी कि त्वरण को। इस मामले में a = 10 m/s2 का मतलब हुआ कि हर एक सेकण्ड में वस्तु के वेग में 10 m/s का इज़ाफा होगा। शुरुआती स्थिति, जिस समय वस्तु का वेग 20 m/s था, से हर एक सेकण्ड में वस्तु का वेग 10 m/s बढ़ जाएगा। पहले सेकण्ड बाद वस्तु का वेग 20 + 10 = 30 m/s, दूसरे सेकण्ड बाद 30 + 10 = 40 m/s और इस तरह आगे भी बढ़ता जाएगा (तालिका 1)। गौर दीजिए कि समीकरण (2) में  a=  10  m/s2  व  u = 20 m/s के  लिए  t = 0, 1, 2, 3, 4, 5... सेकण्ड रखने पर हमें वेग (V) के वही मान मिलते जो हमें तालिका 1 में मिले।

(2) लाइन L2: इस लाइन के लिए भी y-अन्त:-खण्ड या शुरुआती वेग 20 m/s है। लेकिन ढलान, जो कि इस लाइन पर कोई भी दो बिन्दु लेकर निकाली जा सकती है, -10 m/s2 है। जिसका मतलब हुआ कि जिस गति को यह लाइन दर्शा रही है, उसके लिए त्वरण a=-10 m/s2 होगा;  यानी कि हर एक सेकण्ड में वस्तु का वेग 10 m/s कम हो जाएगा। आगे की ओर 20 m/s के शुरुआती वेग से बढ़ती हुई वस्तु का वेग एक सेकण्ड बाद घटकर 10 m/s हो जाएगा। क्योंकि वेग अब भी धनात्मक है, इसलिए वस्तु आगे की ओर ही बढ़ रही होगी। अगले एक सेकण्ड बाद वस्तु का वेग 10 m/s से घटकर शून्य हो जाएगा; यानी कि ठीक इस क्षण में वस्तु स्थिर होगी। अगले एक सेकण्ड बाद वस्तु का वेग होगा -10 m/s, यानी कि अब वस्तु उल्टी दिशा में या फिर पीछे की ओर बढ़ रही होगी। चार सेकण्ड बाद वस्तु का मान होगा -20 m/s. इस तरह आने वाले समय में वस्तु का वेग विपरीत दिशा में लगातार बढ़ता जाएगा (तालिका 2)।   समीकरण   (2)   में a = -10 m/s2 व u= 20 m/s रखने से मिलने वाला सम्बन्ध होगा:
v = -10t + 20
इस समीकरण में द्य के अलग-अलग मान रखने पर हमें तालिका 2 में दर्शाए वेग ही मिलते।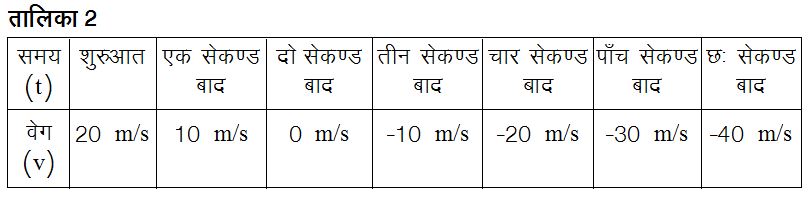
क्या आपने ऐसी किसी गति का अवलोकन किया है जिसमें वस्तु का वेग आगे बढ़ते हुए घटता जाए और फिर किसी क्षण शून्य हो जाए, जिसके बाद वस्तु विपरीत दिशा में गति करने लगे व उसका वेग इस विपरीत दिशा में लगातार बढ़ता जाए? मुझे तो पूरा यकीन है कि आपने ऐसी गतियाँ ज़रूर देखी होंगी। ज़रा सोचिए। पहले व दूसरे, दोनों मामलों में त्वरण पूरी गति के लिए समान है, इसलिए ऐसी गतियाँ एकसमान त्वरित गति का उदाहरण हैं।

(3) लाइन L3: इस लाइन के लिए भी y-अन्त:-खण्ड या शुरुआती वेग 20 m/s है। लेकिन इसकी ढलान a = 0 m/s2 शून्य है जिसके कारण वस्तु के शुरुआती वेग में समय के साथ कोई भी परिवर्तन नहीं आएगा। वस्तु जिस वेग से आगे की ओर बढ़ना शुरु  हुई थी उसी वेग से लगातार आगे बढ़ती जाएगी। समीकरण (2) में a = 0 m/s2 व u = 20 m/s रखने से मिलने वाला सम्बन्ध होगा:
v = 0t + 20
इस सम्बन्ध से साफ ज़ाहिर है, इस गति के दौरान समय के किसी भी मान के लिए वेग ध्, 20 थ्र्/द्म के बराबर होगा यानी कि यह गति एकरूप वेग की गति होगी।

दर की दर तो ठीक लेकिन दूरी का क्या?
इतनी बातचीत के बाद एक जायज़ सवाल बनता है कि वेग और त्वरण तो ठीक है, लेकिन वस्तु ने इन गतियों के दौरान दूरी कितनी तय की या सन्दर्भ बिन्दु से उसकी दूरी कितनी थी? आखिरी मामले के लिए जिसमें त्वरण शून्य यानी कि गति एकरूप वेग की गति है, इन दूरियों को निकालना बहुत आसान होगा। हम इस सीरीज़ के दूसरे भाग (गति के ग्राफ और लाइनें, संदर्भ अंक-105) में देख चुके हैं कि एकरूप वेग से चलने वाली वस्तु एक निश्चित दिशा में बराबर समय अन्तराल या अवधि में समान दूरी तय करती है। यानी कि अगर वस्तु 20 m/s के एकरूप वेग से आगे बढ़ रही है तो हर एक सेकण्ड में वह धनात्मक दिशा में 20 m की दूरी तय करेगी - एक सेकण्ड बाद 20 m, दो सेकण्ड बाद 40 m व इसी तरह द्य सेकण्ड बाद 20 mt की दूरी तय कर चुकी होगी। अगर वस्तु की शुरुआती स्थिति को ही सन्दर्भ-बिन्दु मानें तो द्य सेकण्ड के बाद वस्तु की सन्दर्भ-बिन्दु से दूरी भी धनात्मक दिशा में 20 mt के ही बराबर होगी। साफ ज़ाहिर है कि अगर एकरूप वेग u हो तो द्य समय में वस्तु की सन्दर्भ-बिन्दु से दूरी यानी कि विस्थापन होगा ut. क्या हम इस विस्थापन को वेग-समय ग्राफ पर देख सकते हैं? आइए देखते हैं। 20 m/s के एकरूप वेग से चल रही वस्तु के लिए वेग-समय व विस्थापन-समय ग्राफ चित्र-2 में दिखाए गए हैं।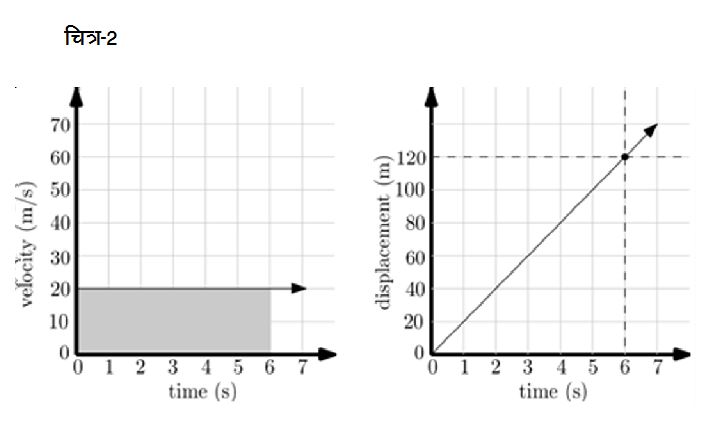
जैसा कि हमने देखा कि 20 m/s के एकरूप वेग से गति कर रही वस्तु सन्दर्भ-बिन्दु से द्य सेकण्ड में 20 mt की दूरी से विस्थापित होगी। इस विस्थापन को हम एक ऐसे आयत के क्षेत्रफल के रुप में भी देख सकते हैं जिसकी चौड़ाई 20 व लम्बाई t है। क्या आप इस आयत को वेग-समय ग्राफ पर देख सकते हैं? t = 6s के लिए चित्र-2 के वेग-समय ग्राफ पर इस आयत को दर्शाया गया है। समय के अक्ष व एकरूप वेग की गति को दर्शा रही लाइन के बीच बने इस आयत के क्षेत्रफल का मान 120 होगा जो 6 s बाद वस्तु के विस्थापन 120 m के बराबर है। क्योंकि इस मामले में वस्तु के चलने की दिशा नहीं बदल रही इसलिए विस्थापन का मान वस्तु के द्वारा तय की गई दूरी के बराबर ही होगा। ऐसे में वस्तु की गति के लिए चाल-समय ग्राफ ठीक वेग-समय ग्राफ जैसा व वस्तु के द्वारा तय किया गया दूरी-समय ग्राफ ठीक विस्थापन-समय ग्राफ के जैसा ही होगा (बनाकर देखिए)।
एकरूप वेग का एक और मामला देखते हैं जिसमें वस्तु पहले तीन सेकण्ड आगे की ओर 20 m/s के एकरूप वेग से चली और फिर बिना वक्त गवाए अगले तीन सेकण्ड 20 m/s के एकरूप वेग से पीछे की ओर चली। साफ तौर पर पहले तीन सेकण्ड वस्तु का वेग होगा +20 m/s व अगले तीन सेकण्ड -20 m/s। चित्र-3 में वेग-समय व चाल-समय ग्राफ पर इस मामले को दर्शाया गया है। इस मामले में पहले तीन सेकण्ड में वस्तु आगे की ओर 60 m की दूरी तय करेगी व फिर अगले तीन सेकण्ड विपरीत दिशा में 60 m. कुल मिलाकर वस्तु के द्वारा तय की गई दूरी इस मामले में भी 120 m ही होगी व वस्तु के द्वारा तय की गई दूरी व समय के बीच का ग्राफ भी चित्र-2 के दूरी-समय ग्राफ जैसा ही होगा। लेकिन इस मामले में 6 s के बाद वापस वस्तु उसी जगह पर होगी जहाँ से उसने शुरुआत की थी। अगर वस्तु की शुरुआती स्थिति पर ही सन्दर्भ-बिन्दु लें तो क्या आप वस्तु की सन्दर्भ-बिन्दु से दूरी (विस्थापन) व समय के बीच का ग्राफ बना सकते हैं? लेख के अन्त में दिए चित्र-7 में इस सवाल का जवाब देखने से पहले कोशिश कीजिए इसे बनाने की।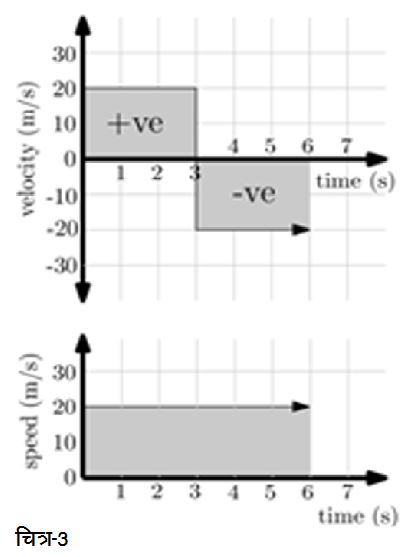

इस चर्चा से जो बात निकलकर आती है वो यह कि एकरूप वेग की किसी गति के वेग-समय ग्राफ व चाल-समय का क्षेत्रफल क्रमश: वस्तु के विस्थापन व तय की गई दूरी के बराबर होता है।
* क्या चित्र-2 की ही तरह दूरी-समय ग्राफ पर हमें एक लाइन मिलेगी?
* अगर हाँ, तो उस लाइन की ढलान क्या होगी?
* अगर नहीं, तो फिर दूरी-समय ग्राफ कैसा होगा?
एक दूरी-समय ग्राफ की लाइन की ढलान वस्तु की एकरूप चाल या वेग को दर्शाती है। लेकिन चित्र-4 की गति के मामले में तो वेग एकरूप नहीं है; बल्कि लगातार बदल रहा है। इसका मतलब हुआ कि दूरी-समय ग्राफ एक लाइन तो नहीं होगा, क्योंकि लाइन की ढलान निश्चित होती है। सवाल अब भी वही कि दूरी-समय ग्राफ कैसा होगा?

क्या इस सवाल का जवाब ढूँढ़ने के लिए हमारे पास कोई संकेत हैं? हाँ - अगर हम यह मान लें कि एकरूप गति के चित्र-2 वाले मामले की ही तरह चित्र-4 के वेग-समय ग्राफ में भी समय के अक्ष व गति को दर्शा रही लाइन के बीच का क्षेत्रफल वस्तु के विस्थापन के बराबर होगा! गैलीलियो ने सत्रहवीं शताब्दी में लगभग ऐसी ही3 अवधारणा मुक्त रूप से एकसमान त्वरण के प्रभाव में गिर रही एक वस्तु की गति की व्याख्या करने के लिए बनाई व अपने प्रयोगों से इसे सही भी पाया। तो हम भी इस अवधारणा को सही मानकर आगे बढ़ते हैं कि वेग-समय ग्राफ का क्षेत्रफल विस्थापन के बराबर होगा। आप चाहें तो गैलीलियो की तरह इस लेख के अन्त में सुझाया गया प्रयोग कर इस अवधारणा की जाँच कर सकते हैं।   
चलिए देखते हैं कि एकसमान त्वरण की गति के लिए वेग-समय ग्राफ का क्षेत्रफल कितना होगा। चित्र-5 में एकसमान त्वरण की गति के लिए वेग-समय ग्राफ दिखलाया गया है। ध्यान दीजिए कि इस ग्राफ में हमने संख्याएँ न लेकर चिन्हों का इस्तेमाल किया है ताकि क्षेत्रफल का एक आम फॉर्मूला निकल सके जो कि शुरुआती वेग (u), एकसमान त्वरण (a) व समय (t) के किसी भी मान के लिए इस्तेमाल किया जा सके।
ग्राफ में वस्तु की दो बिन्दुओं, शुरुआती स्थिति A व t समय बाद की स्थिति ए के बीच के क्षेत्रफल को दर्शाया गया है। इस क्षेत्रफल को दो भागों के क्षेत्रफल के योग के रूप में देख सकते हैं:

क्षेत्रफल (I) = लम्बाई  t व चौड़ाई u के आयत का क्षेत्रफल = t x u
क्षेत्रफल (II) = आधार t व ऊँचाई  at के त्रिभुज का क्षेत्रफल = 1/2 x t x at
इन  दोनों  का  कुल  योग  होगा
            (u x t) + (1/2x t x at)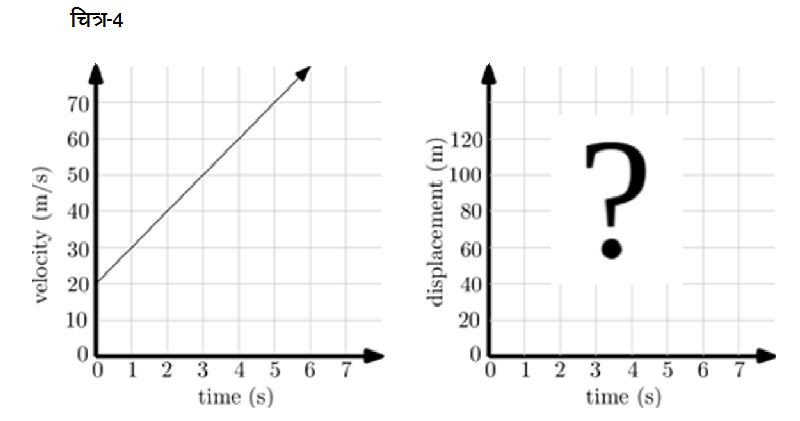
जो हमारी मान्यता के मुताबिक t समय में वस्तु का विस्थापन होगा। अगर इस दूरी को s से दर्शाएँ तो
      s = ut+1/2at2    (3)

समीकरण (3) का पहला भाग शुरुआती वेग के कारण व दूसरा भाग वेग में होने वाले परिवर्तन की दर यानी कि त्वरण के कारण है। अगर त्वरण शून्य हो यानी कि गति एकरूप वेग की हो तो हमें s = ut मिलेगा। इस फॉर्मूले को हम पहले ही देख चुके हैं। अगर शुरुआती वेग शून्य हो तो विस्थापन होगा,
        s=1/2at2     (4)
a = 10 m/s2 व u = 20 m/s के लिए समीकरण (3) से समय t व विस्थापन s के बीच सम्बन्ध होगा:

s = 20t+1/2 10t2

इस फॉर्मूले में t = 0,1, 2, 3, 4, 5... रखकर हम वस्तु के विस्थापन को निकाल सकते हैं। तालिका 3 व चित्र-6 में इन विस्थापनों को दिखलाया गया है।

चूँकि इस मामले में वस्तु एक ही दिशा में बढ़ रही है इसलिए वस्तु के द्वारा तय की गई दूरी व समय के बीच का ग्राफ भी चित्र-6 के जैसा ही होगा।
अच्छा एक बात और। जानते हैं अगर इस विस्थापन-समय ग्राफ के वक्र पर किसी एक बिन्दु पर स्पर्श रेखा खींची जाए तो उस रेखा की ढलान क्या दर्शाएगी? उस बिन्दु के सापेक्ष समय पर वस्तु के वेग को। कैसे और क्यूँ? इनके जवाब आप खुद ढूँढ़िए।
अब वो गैलीलियो का प्रयोग जिसे दोहराकर आप एक समान त्वरण की गति कर रही वस्तु के द्वारा तय की गई दूरी की हमारी अवधारणा की जाँच कर सकते हैं। गैलीलियो ने आनत तल (inclined plane) से धातु के छर्रों को लुढ़काकर अलग-अलग समय-अन्तरालों में छर्रों के द्वारा तय की गई दूरी को मापा था। गैलीलियो का मानना था कि यह गति एक समान त्वरण की गति है जिसमें त्वरण का मान आनत तल की ढलान व गुरुत्वीय त्वरण के मान पर निर्भर करता है। एक ऊँचाई से स्थिरावस्था (शुरुआती वेग शून्य) से छर्रों को एक सीधे पथ पर लुढ़काकर व तय की गई दूरियों को मापकर गैलीलियो इस निष्कर्ष पर पहुँचे कि छर्रे के द्वारा तय की गई दूरी समय के वर्गानुपाती होती है। समीकरण (4) भी यही दर्शाता है। आप भी शायद एक ऐसा ही प्रयोग तैयार कर इस तथ्य को जाँचना चाहें। अगर इस प्रयोग को आप दोहराएँ तो अपने अनुभव हमसे बाँटना मत भूलिएगा।     
और अन्त में वो एक सवाल जो पिछली दफे होशंगाबाद में एकलव्य द्वारा  आयोजित  शिक्षक-प्रशिक्षण कार्यशाला में एक सत्र के संचालन के दौरान हमारे मित्र भौतिकी विशेषज्ञ भास बापट ने अपने हाथ में पकड़ी चॉक को हवा में उछालते हुए सहभागियों से पूछा था। क्या आप ऊपर की ओर उछाली गई चॉक की गति से जुड़े ग्राफ (विस्थापन-समय, दूरी-समय, वेग-समय व चाल-समय ग्राफ) बना सकते हैं? संकेत के लिए बता दूँ कि चित्र-1 के ग्राफ की लाइन L2 इस सवाल का जवाब तैयार करने में आपकी मदद कर सकती है।

विवेक मेहता: आई.आई.टी., कानपुर से मेकेनिकल इंजीनियरिंग में पीएच.डी. की है एवं तेज़पुर विश्वविद्यालय, असम में पढ़ा रहे हैं। एकलव्य के विज्ञान शिक्षण कार्यक्रम के तहत वे हाईस्कूल की कक्षाओं के लिए गतिविधि आधारित मॉड्यूल तैयार कर रहे हैं। यह प्रयास, कनेक्ट्ड लर्निंग इनिशिएटिव, टाटा सामाजिक विज्ञान संस्थान के समर्थन से संचालित है।
आभार: कनेक्ट्ड लर्निंग इनिशिएटिव टीम के सभी साथियों - राजेश, दीपक, भास, उमा व हिमांशु का, जिनके सुझावों के चलते यह लेख अपने वर्तमान रूप में आ पाया।