Select any text and click on the icon to listen!
ByGSpeech

चितियों का निर्माण यानी ईंटों का जोड-घटा

रामकृष्ण भट्टाचार्य

प्राचीन भारत की ज्यामिती                                                                                                                                                        भाग 6 

पिछली बार हमने चिति निर्माण में उपयोगी प्रमेयों को देखा तो यह अहसास होने लगा कि चितियों को बनाने में कितनी ज्यामिति की आवश्यकता होती थी। लेकिन इसके बाद मसला थोड़ा टेढ़ा है क्योंकि चिति का आकार तो महत्वपूर्ण था ही, साथ ही चिति का क्षेत्रफल और उसकी प्रत्येक परत में लगाई जाने वाली ईंटों की संख्या भी निश्चित थी। इन सबका ध्यान रखते हुए भी चितियों को कलात्मक व आकर्षक बनाने की कोशिश लगातार होती रही।
श्येन चिति को प्रकृति या सभी चितियों का मूल कहा गया है, ऐसी क्यों? यदि हम प्रथम प्रकार अर्थात चतुरस्र श्येन चिति को देखें तो इस क्यों का जवाब मिलने लगता है। यह सबसे प्राचीन स्वरूप है जिसे चार प्रकार की वर्गाकार ईटों से बनाया जाता है। इन चार प्रकार की ईंटों को चतुर्थी, पंचमी, षष्ठी व दशमी कहते हैं क्योंकि इनकी भुजाएं क्रमशः एक पुरुष की 1/4, 1/5, 1/6 व 1/10 होती हैं। दूसरे प्रकार की श्येन चिति में वर्गाकार पंचमी और दशमी ईंटों के अलावा दो अलग-अलग किस्म की आयताकार ईंटों का भी उपयोग होता है। उपरोक्त चार प्रकार की 160, 2, 8 व 30 ईटे नीचे चित्र में दर्शाए अनुसार जमाना है। इससे गरूड़ का धड़, डैने और पूंछ बन जाते हैं। (चित्र1, तालिका-1)। यह सही है कि उक्त आकृति हूबहू गरूड़ जैसी तो नहीं है। किन्तु चतुरस्र श्येन चिति की सबसे निचली परत शुरुआत में इसी तरह बनाई गई थी। तीसरी व पांचवीं परत में ईंटों की व्यवस्था समान होती है।

दूसरी व चौथी परतों में इसी तरह की 165, 4, 6 व 25 ईंटें लेकर
          

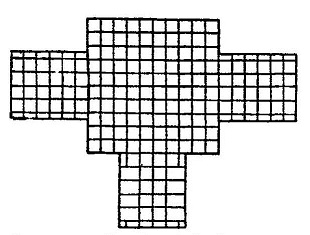
तालिका:1 चतुर्सरा श्येन चिति (प्रकार: 2, परत 1,3,5)
क्र. आकार भुजाएं क्षेत्रफल ईटों की संख्या कुल क्षेत्रफल
1. वर्ग 24 576 160 92160
2. आयात 24,36 864 8 6912
3. आयात 12,24 288 30 8640
4.   वर्ग 12 144  2 288
योग 200 108000
 
तालिका:2 चतुर्सरा श्येन चिति (प्रकार: 2, परत 2,4)
क्र. आकार भुजाएं क्षेत्रफल ईटों की संख्या कुल क्षेत्रफल
1. वर्ग 24 576 165 95040
2. आयात 24,36 864 6 5184
3. आयात 20 288 25 17200
4. वर्ग 12 144 4 576
  योग 200 108000

उन्हें प्रस्तुत चित्र के अनुसार जमाना है। अब अनुष्ठान की समस्त शर्ते पूरी हो गई हैं: प्रत्येक परत में 200 ईंटें हैं अर्थात् पूरी चिति में कुल 1000 ईंटें हुईं और इसका क्षेत्रफल 7.5 पुरुष यानी 1,08,000 वर्ग अंगुल हुआ। (चित्र-2, तालिका-2)
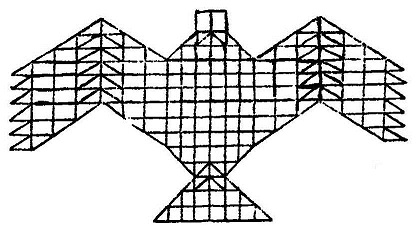यजुर्वेद के मैत्रायणिया मत में आयताकार ईंटों का उपयोग वर्जित है। आयताकार ईंटों का उपयोग धर्म निरपेक्ष इमारतों (जैसे घर आदि) के निर्माण में होता है, धार्मिक अनुष्ठान से संबंधित संरचनाओं में नहीं। अलबत्ता ईंटों के प्रकार में इस परिवर्तन ने पक्षी -आकार की श्येन चिति के निर्माण में परिष्कार व कलात्मकता का मार्ग प्रशस्त किया। यजुर्वेदी ब्राह्मणों ने घोषणा की कि अग्नि का निर्माण पक्षी की प्रतिमा के रूप में होता है। बौधायन में इस विचार की व्याख्या यों की गई है कि 'यह (अग्नि) उड़ते हुए पक्षी की छाया के अनुरूप बनाई जाना चाहिए'; हालांकि चिति में पांच परतें हैं किन्तु महत्व मात्र पांचवी (यानी सबसे ऊपरी) परत का है: ऊपर से देखने पर यह किसी उड़ते हुए पक्षी की छाया समान दिखाई देनी चाहिए। अब स्थिति यह थी कि उड़ते पक्षी या उसकी छाया से साम्य न तो पहले प्रकार की श्येन चिति का था, न दूसरे प्रकार की। यजमान को तो पुरोहित पर विश्वास रखना पड़ता था कि जो संरचना बनी है वह श्येनचिति है।

अब एक कलाकार आया जिसने पक्षी की एक श्येन चिति बनाई जिसमें सिर था (जो दोनों चतुरस्र चितियों में नदारद था), मुड़े हुए डैने थे और फैली हुई पूंछ थी (जो चतुरस्र चितियों



तालिका:3 श्येन चिति (प्रकार: 2, परत 1, 3, 5) पक्षी के आकार की
क्र.  आकार भुजाएं ऊंचाई  क्षेत्रफल ईटों के संख्या कुल क्षेत्रफल 
1.   वर्ग   24   576  54  31104
2.  आयात   24,36   864  40  34860
3.  आयात  24,30   720  2  1440
4. तिकोनी 24,24,24√2 24 288 28  8464
5.  तिकोनी 24,36,12√13   36 432 76 32832
    योग  200   108000

में प्रतीक रूप में ही थे)। पक्षी आकार की यह चिति प्रकृति के ज्यादा अनुरूप थी और दिखने में अधिक लुभावनी थी। चतुरसु श्येन चित का निर्माण तो कोई ज्यामितिकार कर सकता था किन्तु पक्षी आकार की चिति बनाने में कलाकार की जरूरत होती थी। ये चितियां भी दो प्रकार की होती थीं। चित्र-3, तालिका-3 ।
इन्हें बनाने के लिए आयताकार के अलावा त्रिभुजाकार ईंटों की भी जरूरत होती थी। अन्यथा डैनों को इतना प्राकृतिक रूप में दर्शाना संभव नहीं था। अनुष्ठान के निर्देशों से प्रथम विचलन तो तब हुआ जब अग्नि के निर्माण मानुष (यानी आयताकार) ईंटों का प्रयोग शुरू हुआ। और अब तो अन्य आकृतियां रची व उपयोग की जाने लगीं। तो समय के साथ वर्गाकार के अलावा अन्य आकृतियों की ईंटें भी प्रचलन में आती गईं। दरअसल वक्रपक्ष व्यवस्पुच्छ श्येन चिति में तो एक समलम्बक ईंट का उपयोग भी किया जाता है।
पक्षी आकार की इन चितियों के रचियता की अक्लमंदी गौरतलब है। उसे ईंटों की संख्या और चिति के क्षेत्रफल दोनों मर्यादाओं का ध्यान रखना है, चाहे चिति की आकृति कुछ भी हो। इसी प्रकार से किसी भी परत में ईंटों को इस तरह जमाना होगा कि वे अपने से निचली परत की ईंटों के बीच की खाली जगह या जोड़ों को ढंक लें। और किसी भी हालत में वह अग्नि की सममित व्यवस्था के साथ छेड़छाड़ नहीं कर सकता। यदि ऐसे कठोर नियम न होते तो काम बहुत आसान होता। उदाहरण के लिए श्मशान चिति को देखा जा सकता है (जिसका पार्श्व चित्र अंक 31, पृष्ठ 65 पर दिया जा चुका है)।
यह समलम्बक के आकार की चिति होती है। इसकी समान्तर भुजाएं क्रमशः 2 व 3 पुरुष लम्बी होती हैं और ऊंचाई 6 पुरुष होती है। किन्तु यहां पुरुष का अर्थ रेखीय माप (120 अंगुल) से न होकर क्षेत्रफल के माप से है। यह छोटा पुरुष है जो 84 अंगुल 20 तिल के बराबर है। चिति के लिए ईंटों की जमावट निम्नानुसार होगी। देखिए तालिका 4 एवं 5।
यहां तक तो सब ठीक-ठाक है। परन्तु सवाल है कि विभिन्न ईंटों की आकृतियों व आकारों का निर्धारण कैसे होता था? बौधायन इस संबंध में विस्तृत जानकारी प्रदान करता है। यह जानकारी निम्नानुसार हैः 7.5 पुरुष (108,000 वर्ग अंगुल) के वर्ग को 15 बराबर-बराबर वर्गों में बांटिए। प्रत्येक का क्षेत्रफल 108000/15 = 7200 वर्ग अंगुल होगा। अब एक आयत बनाइए जिसकी भुजाएं क्रमशः
 
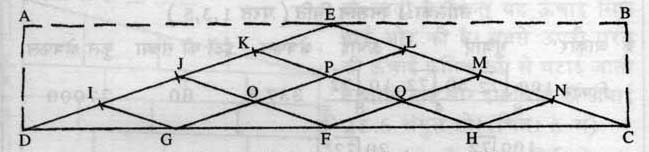√7200/2 यानी 10 /√72/2 तथा √7200/3 यानी 10 /√72/3 हों। (देखिए चित्र-4)
इस आयत (ABCD) में E (AB के मध्य बिन्दु) तथा C और D जोड़कर तीन त्रिभुज बनाइए। रेखा EC व CD को चार बराबर-बराबर भागों में बांटिए और फिर LG, ME, NH, HK, FJ तथा GI को जोड़ दीजिए। त्रिभुज ECD का क्षेत्रफल हैः
1/2x3x10√72 x 10√72 X1/2 = 3/4 (7200 )
= 5400 वर्ग अंगुल
यह पूरे बड़े वर्ग के 1/20 भाग को ढंकेगा।

अब इस तरह विभाजित त्रिभुज से हमारे पास छ: उभयतः प्रउग तथा चार प्रउग आकार की ईंटें हैं। प्रत्येक उभयतः ईंट का क्षेत्रफल 675 वर्ग अंगुल तथा प्रत्येक प्रउग ईंट का क्षेत्रफल 337.5 वर्ग अंगुल है। अतः श्मशान चिति की पहली परत 120 उभयतः प्रउग तथा 80 प्रउग ईंटों से बन जाती है और इनका कुल क्षेत्रफल 7 (1/2)पुरुष होता है।
दूसरी परत को पहले एक आयत व उसके दोनों ओर दो त्रिभुजों में बांट दिया जाता था। प्रत्येक समकोण त्रिभुज को तीन महाचतुस्र और तीन महाप्रउग बृहति ईंटों से ढंक दिया जाता है। आयत को 100 व 88 अर्ध्या ईंटों से ढंका जाता है। (चित्र-5)।
गौरतलब है कि पहली (या तीसरी या पांचवीं) परत को एक समान आकार व आकृति की 320 प्रउग ईंटों से भी ढंका जा सकता है। इसी प्रकार से दूसरी (और चौथी) परत के लिए 6 महाचतुस्र और 6 महाप्रउग के अलावा 144 बृहति ईंटों की जरूरत होगी। किन्तु इनमें से किसी भी विकल्प को अपनाएं, नियम का उल्लंघन होगा। दोनों ही मामलों में ईंटों की संख्या निर्धारित 200 से कम या ज्यादा हो जाएगी। इसलिए उभयतः प्रउग ईंटें (प्रउग को दोहरा

तालिका: 4 श्मशान चिति ( परत 1,3,5 )
क्र.   आकार भुजाएं ऊंचाई क्षेत्रफल ईटों की संख्या कुल क्षेत्रफल
1. तिकोन (100√72)(30√72) (10√72) 337.5 80 27000
2. समलंबक     675 120  81000
योग 200 108000
 
तालिका: 5 श्मशान चिति ( परत 2,4 )
क्र. आकार भुजाएं ऊंचाई क्षेत्रफल ईटों की संख्या कुल क्षेत्रफल
1. आयात (10√72)/4(10√72)/3 (10√72)/4 600 100 60000
2. आयात (10√72)/4 (10√72)/6 (10√72)/4 300 88 26400
3. तिकोन (20√72)  (10√72)/6 (10√290) 1200 6 7200
4. आयात (20√72) (10√72)    2400  6  14000
योग 200 108000

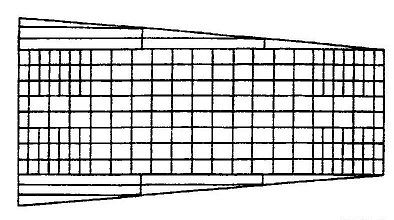चित्र--5 : श्मशान चिति की चौथी परत जिसमें आयात को 188 ईटों से बनाया गया है। शेष 12 ईटें इस आयात के दोनों और बनाए गए समकोण त्रिभुज को बनाने मे इस्तेमाल की गयी है। 

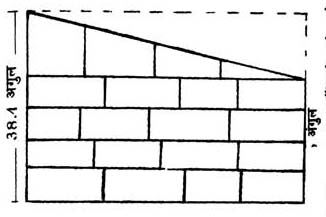चित्र-5 अः श्मशान चिति की पांचवीं परत और अंतिम परत को ढालदार बनाना होता है इसलिए इस परत में कुछ ईंटों की ऊंचाई ज्यादा होती थी और कुछ की कम। एक पूरी बनी चिति में दाईं ओर ऊंचाई 38.4 अंगुल होना चाहिए तथा बाईं ओर 25.6 अंगुल होना चाहिए।

करके) और अध्यबृहति (बृहति की आधी) ईंटें बनाना पड़ती थीं। अन्य चितियों में 200 की जादुई संख्या को पूरा करने के लिए ईंटों को छोटा-बड़ा करना ज़रूरी हो जाता है।
श्मशान चिति में एक और रोचक बात है। इस चिति के अलावा शेष समस्त चितियों में 5 परतों की कुल ऊंचाई घुटने तक (यानी 32 अंगुल) होनी चाहिए और प्रत्येक परत की ऊंचाई 32/5 अंगुल होनी चाहिए। किन्तु श्मशान चिति के मामले में सबसे ऊपरी परत थोड़ी अलग होती है। यहां इसकी ऊंचाई (32/5) x2 = 12.8 अंगुल हो, ऐसा निर्देश है। इस तरह से चिति की कुल ऊंचाई 38.4 अंगुल हो जाती है। किन्तु यह ऊंचाई सिर्फ बाईं ओर की है। सबसे ऊपरी परत की ऊंचाई क्रमिक रूप से घटाई जाती है। ताकि दाईं और इस चिति की ऊंचाई 25.6 अंगुल हो। (चित्रः 5 अ)
किन्तु इससे श्मशान चिति के कुल आयतन में कोई फर्क नहीं पड़ेगा। इसका आयतन तो 34,56,000 घन अंगुल
(108,000 x 25.6) + 108,000 x 12.8 x 1/2) = 108,000 (25.6 + 6.4) = 108000 x 32 अंगुल रहेगा।

हमने पहले ही दिखा दिया है कि यजुर्वेद तथा ब्राह्मणों में स्पष्ट निर्देश न होने की वजह से श्रौत और शुल्व सूत्रों को कुछ चितियां बनाने के वैकल्पिक निर्देश देना पड़े। उदाहरणार्थ बौधायन में द्रोण व कूर्म चिति बनाने के लिए दो अलग-अलग निर्देश दिए। गए हैं। निर्देशों के प्रथम समूह में वर्गाकार (चतुरस्र) चिति तथा दूसरे समूह में वृत्ताकार (परिमण्डल) चिति बनाने का उल्लेख है। इनका अध्ययन करने से पूर्व वृत्ताकार चिति दो प्रकार के रथचक्र पर नज़र डालें। प्रथम किस्म का रथचक्र वह होता है जिसमें प्रधि अर्थात पहिए की परिधि के वर्गाकार खण्ड होते हैं तथा दूसरे किस्म का रथचक्र वह होता है जिसमें अर अर्थात ताड़ियां होती है। (चित्रः 6 एवं 7)
इन चितियों को बनाने के लिए
                              
               
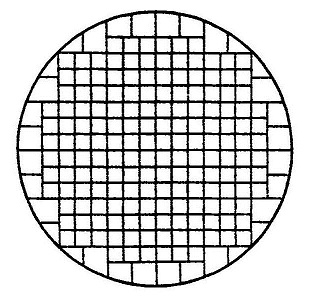
चित्र-6 एवं 7: पहले प्रकार की रथचक्र चिति जिसमें अर या ताड़ियां नहीं होती। बल्कि वृत परिधि के ही वर्गाकार खंड होते हैं।
     
                                         
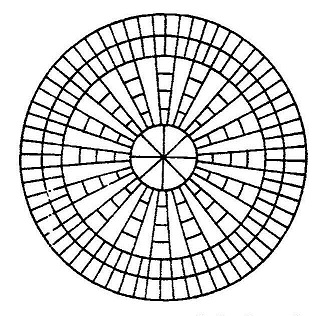
चित्र-8 एवं 9: रथचक्र चिति को बनाने का दूसरा तरीका जिसमें अर या ताड़ियां बनाई जाती हैं। रथचक्र चिति को बनाने के लिए विशेष ईंटों की जरूरत होती जिनका एक फलक वक्राकर होना चाहिए।

विशेष प्रकार की ईंटों की आवश्यकता होती है। इन ईंटों का एक फलक वक्राकार होता है जबकि शेष तीन फलक सपाट होते हैं। चित्रों से बात और स्पष्ट हो जाएगी। (चित्र 8-9)
इसके बाद द्रोण चिति
                                    

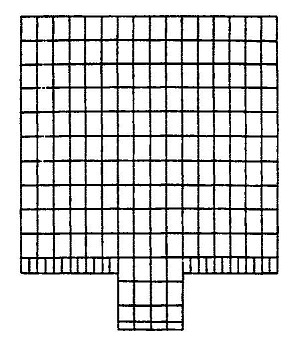
तालिका: 6 द्रोण चिति ( परत 1,3,5) रेक्टिलिनियर 
 क्र.   आकार  भुजाएँ  क्षेत्रफल    ईटों की संख्या  ईटों की संख्या
1. आयात  20,30 600 168 1008000
2. वर्ग 20 400 4 1600
3. आयात 10,20 200  28  5600
    योग  200 108000
 
तालिका: 7 द्रोण चिति ( परत 2,4 ) रेक्टिलिनियर 
क्र.  आकार भुजाएँ   क्षेत्रफल ईटों की संख्या   कुल क्षेत्रफल
1. वर्ग 30 900 22 19800
2. आयात 20,30 600 124 74400
3. वर्ग 20 400 15 6000
4. आयात 10,20 200   39  7800
योग 200 108000

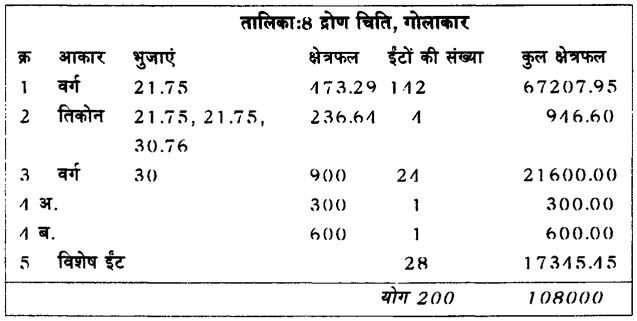(आयताकार) को देखिए। इसमें किसी विशेष हुनर की ज़रूरत नहीं है, सिवाय इसके कि इसकी वर्गाकार काया के साथ इसे कठौती का रूप देने के लिए इसमें एक हैण्डल (टोंटी) लगाना होती है। दिए गए चित्र व तालिका से स्पष्ट हो जाएगा कि यह कैसे किया जाता है। देखिए चित्र 10 एवं 11 तालिका 6 व 7।
अब देखें वृत्ताकार द्रोण चिति को। प्रमेय क्रमांक 13 की मदद से हमें 107,100 वर्ग अंगुल का एक वृत्त खींचना होगा। गुर यह है: यदि हम 108,000 वर्ग अंगुल क्षेत्रफल का वर्ग बनाते, तो हमें 120 बृहति ईंटों की ज़रूरत पड़ती (प्रत्येक बृहति ईंट का क्षेत्रफल 900 वर्ग अंगुल होता है, अर्थात उसकी प्रत्येक भुजा 30 अंगुल होती है, यानी ये समस्त चतुर्थी ईंटें होती)। यदि हम ऐसी एक ईंट हटा दें तो 107100 वर्ग अंगुल का वर्ग बचा रहेगा। जब इस वर्ग को वृत्त में तब्दील करते हैं तो इस बची हुई ईंट को AB के मध्य में रख देते हैं ताकि जब वर्ग को वृत्त में बदला जाए तो यह दो भागों (2/3 व 1/3) में बंट जाए। इन दो भागों को दो अलग-अलग ईंट मानकर चलना होता है।

अब इस वृत्त के अन्दर बन सकने वाला बड़ा-से-बड़ा वर्ग बनाया जाता है और इस वर्ग को 144 छोटे-छोटे वर्गों में बांटा जाता है। वृत्त के आठ खण्डों में से प्रत्येक 7 विशेष ईंटों (जिनका एक फलक वृत्ताकार हो) और छः बृहति ईंटों से ढंका जाता है। (देखिए चित्र-12)। अर्थात हमारे पास वर्ग को भरने के लिए 144 वर्गाकार ईंटें हैं, परिधि बनाने के लिए 28 (7x4) विशेष ईंटें हैं और 24 (4 x 6) ऐसी बृहति ईंटें हैं जो खण्ड के पैंदे
                                    
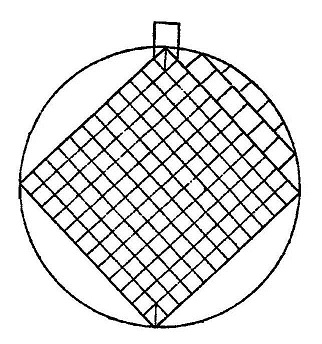
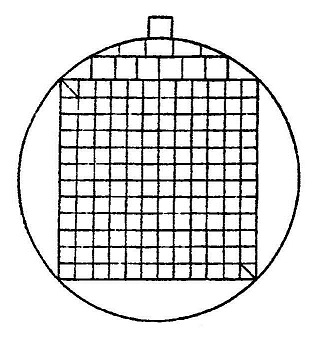
चित्र-12: वृत्ताकार द्रोण चिति की पहली परत में ईंटों की जमावट।
चित्र-13: वृत्ताकार द्रोण चिति की अगली परत बनाने के वर्ग को 45 डिग्री घुमा देते हैं।

में होंगी और वर्ग की भुजाओं को स्पर्श करेंगी।
इस तरह, हमारे पास कुल 144+28+24 = 196 ईंटें हैं। यदि हम इसमें छूटी हुई बृहति ईंट के दो टुकड़े जोड़ दें तो मात्र 198 ईंटे होती हैं। अभी भी आवश्यक संख्या से 2 ईटें कम हैं। अतः बड़े वर्ग की दो छोटी ईंटों को 2-2 भागों में बांटना होगा। इसके फलस्वरूप 4 तिकोनी ईंटें बनेंगी। परिणाम तालिका-8 में दर्शाया गया है।
दूसरी परत में किसी पुनर्व्यवस्था की आवश्यकता नहीं है, सिवाय इसके कि वर्ग को 45 अंश से घुमाकर बनाया जाए। (चित्र-13)
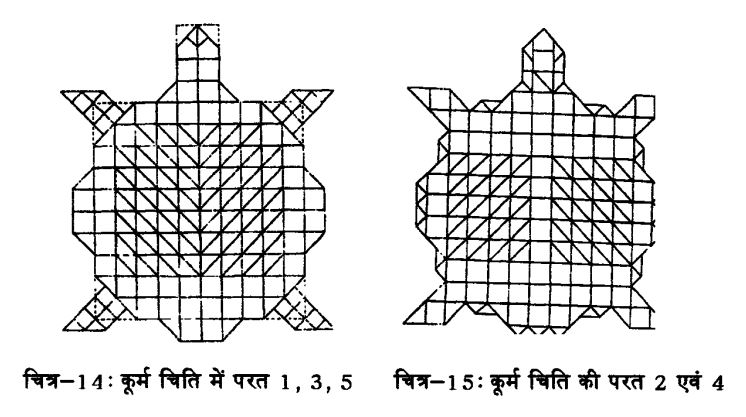
आइए कूर्म चिति को देखें। चतुर्भुजाकर कूर्म चिति तो कला का नमूना होती है। पक्षी आकार चिति की ही तरह इसकी कल्पना भी किसी ज्यामितिविद ने नहीं बल्कि ज्यामितिविद कलाकार ने की होगी। उसने अपने मन की आंखों से देखा होगा कि चतुर्थी ईंटों (30 x 30 वर्ग अंगुल क्षेत्रफल ) व उनके हिस्सों की एक निश्चित संख्या तथा एक हंसमुखी ईंट मिलकर हूबहू कछुए की छवि निर्मित कर सकेंगे। नीचे दिए गए चित्र तालिकाएं स्वयं पूरी कहानी कह देते हैं। चित्र 14 एवं 15 तथा तालिका 9 एवं 10 देखिए।

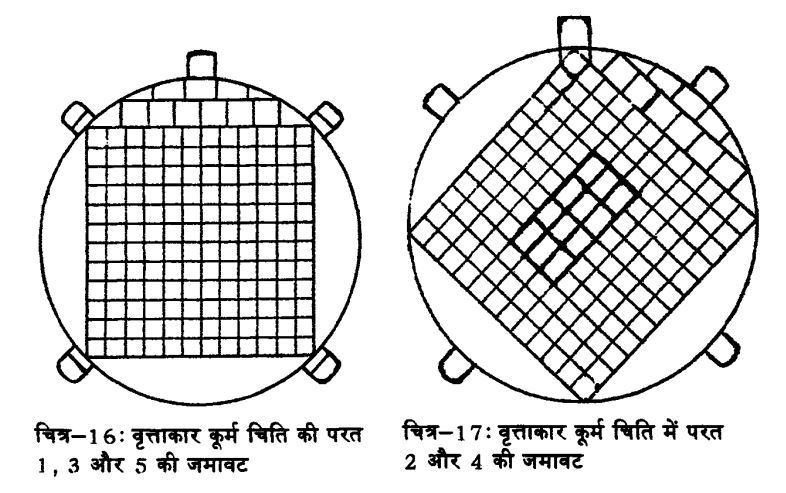
वृत्ताकार कूर्म चिति में इतनी सुन्दरता नहीं होती। किन्तु इसमें भी कुछ हुनर अवश्य लगता है। इसमें भी विधि वही होती है जो वृत्ताकार द्रोण चिति में प्रयुक्त की गई थी। किन्तु एक बृहति (चतुर्थी) ईंट छोड़ने की बजाए हम पांच ऐसी ईंटों को बाहर छोड़ देते हैं और उन्हें 10 (5x2) भागों में बांटते हैं। इन ईंटों को हटाने के बाद जो वर्ग बचता है उसका क्षेत्रफल 103,500 वर्ग अंगुल (108,000-900 x 5 वर्ग अंगुल) होता है। इसे वृत्त में तब्दील किया जाता है। इस वृत्त के अन्दर बन सकने वाला बड़ा-से-बड़ा वर्ग बनाकर उसे 144 बराबर वर्गों में बांटा जाता है। चित्र 16 को देखिए।
वर्ग के बाहर के खण्डों को 28 विशेष ईंटों तथा 24 बृहति ईंटों से भरा जाता है। ऐसा करने पर ईंटों की संख्या 144+28+24+10= 206 हो जाती है जो निर्धारित से 6 ज्यादा हैं।
इन 6 अतिरिक्त ईंटों ने कलाकार को कतई परेशान नहीं किया। कछुए के सिर और पैर का ढाचा बन जाने के बाद कलाकार ने तय किया कि 18 वर्गाकार ईंटों को निकालकर उनके स्थान पर 12 वर्गाकार ईंटें रख दी

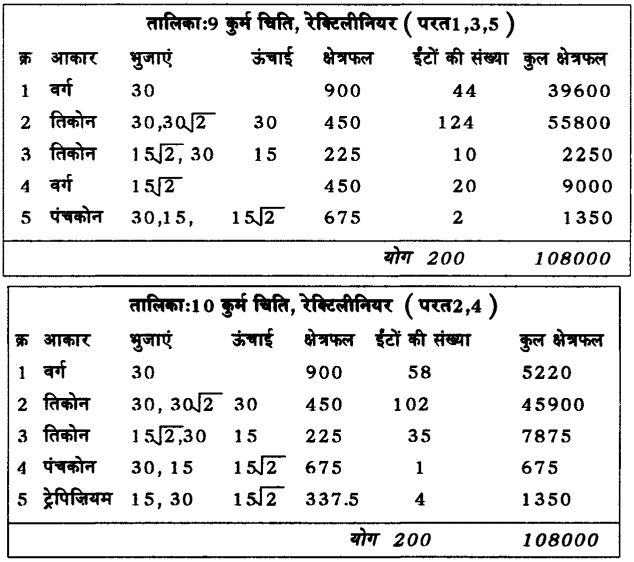
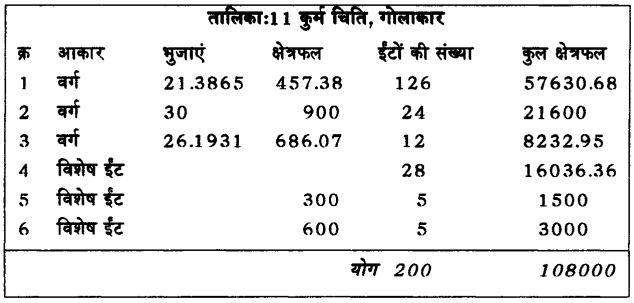जाएं। इन बड़ी ईंटों का क्षेत्रफल 1x (1/2) गुना हो। इस प्रकार से अतिरिक्त ईंटों की समस्या सुलझ जाती है। चित्र 17, तालिका 11 को देखिए।
जो वर्ग बनाया गया था उसे 45 अंश से घुमाना पड़ता है ताकि चार कोने पूर्व, दक्षिण, पश्चिम व उत्तर की ओर रहें। अर्थात कूर्म चिति की दो परतें द्रोण चिति से ठीक उल्टी होती हैं।
चितियों का इतना विवेचन काफी है। आपस्तम्ब व मानव शुल्व सूत्रों में चितियां बनाने की वैकल्पिक विधियां दी गई हैं किन्तु ये बौधायन शुल्ब सूत्र से बहुत अलग नहीं हैं। अब वक्त आ गया है कि हम ईंटों की बात करें।

रामकृष्ण भट्टाचार्यः आनंद मोहन कॉलेज, कलकत्ता के अंग्रेज़ी विभाग में रीडर तथा कलकत्ता विश्वविद्यालय में अंग्रेजी पाठ्यक्रम में अतिथि लेक्चरर। विज्ञान लेखन में रुचि।।
अनुबादः सुशील जोशीः एकलव्य के होशंगाबाद विज्ञान शिक्षण कार्यक्रम से जुड़े हैं। साथ ही स्वतंत्र लेखन एवं अनुवाद करते हैं।

Select and listen
J! InfoRequestSessionProfileQueries143Log
14.295MBMemory Usage218msRequest Duration
Joomla! Version4.4.5
PHP Version8.1.31
Identityguest
Response200
Templatej51_maya
Database
Server
mysql
Version
8.0.40
Collation
utf8mb4_0900_ai_ci
Conn Collation
utf8mb4_0900_ai_ci
$_GET
[]
$_POST
[]
$_SESSION
array:1 [ "joomla" => "***redacted***" ]
$_COOKIE
[]
$_SERVER
array:56 [ "USER" => "eklavyaco" "HOME" => "/home/eklavyaco" "PATH_TRANSLATED" => "/home/eklav...
session
array:3 [ "counter" => 1 "timer" => array:3 [ "start" => 1744127258 "last" => 1744127258...
registry
array:3 [ "data" => [] "initialized" => false "separator" => "." ]
user
array:18 [ "id" => 0 "name" => null "username" => null "email" => null "password" => "***r...
  • afterLoad (542.17KB) (3.63ms)
  • afterInitialise (1.31MB) (28.15ms)
  • afterRoute (3.17MB) (20.09ms)
  • beforeRenderComponent com_content (73.16KB) (3.47ms)
  • Before Access::preloadComponents (all components) (34.2KB) (836μs)
  • After Access::preloadComponents (all components) (119.27KB) (2.93ms)
  • Before Access::preloadPermissions (com_content) (4.16KB) (36μs)
  • After Access::preloadPermissions (com_content) (3.54MB) (16.6ms)
  • Before Access::getAssetRules (id:2851 name:com_content.article.2249) (258.8KB) (236μs)
  • After Access::getAssetRules (id:2851 name:com_content.article.2249) (8.47KB) (127μs)
  • afterRenderComponent com_content (771.66KB) (28.63ms)
  • afterDispatch (2.28KB) (196μs)
  • beforeRenderRawModule mod_menu () (1.99MB) (51.24ms)
  • afterRenderRawModule mod_menu () (1.13MB) (12.09ms)
  • beforeRenderModule mod_menu () (696B) (16μs)
  • afterRenderModule mod_menu () (26.88KB) (173μs)
  • beforeRenderRawModule mod_menu () (24.38KB) (51μs)
  • afterRenderRawModule mod_menu () (26.45KB) (2.68ms)
  • beforeRenderModule mod_menu () (696B) (10μs)
  • afterRenderModule mod_menu () (26.27KB) (122μs)
  • beforeRenderRawModule mod_menu () (24.48KB) (40μs)
  • afterRenderRawModule mod_menu () (65.22KB) (128μs)
  • beforeRenderModule mod_menu () (696B) (3μs)
  • afterRenderModule mod_menu () (1.64KB) (60μs)
  • beforeRenderRawModule mod_menu (More) (19.64KB) (680μs)
  • afterRenderRawModule mod_menu (More) (12.04KB) (475μs)
  • beforeRenderModule mod_menu (More) (704B) (9μs)
  • afterRenderModule mod_menu (More) (12.94KB) (488μs)
  • beforeRenderRawModule mod_menu (Gallery) (16B) (73μs)
  • afterRenderRawModule mod_menu (Gallery) (13.38KB) (337μs)
  • beforeRenderModule mod_menu (Gallery) (704B) (6μs)
  • afterRenderModule mod_menu (Gallery) (2.98KB) (85μs)
  • beforeRenderRawModule mod_menu (Magazine) (32B) (45μs)
  • afterRenderRawModule mod_menu (Magazine) (21.47KB) (259μs)
  • beforeRenderModule mod_menu (Magazine) (704B) (4μs)
  • afterRenderModule mod_menu (Magazine) (12.3KB) (397μs)
  • beforeRenderRawModule mod_menu (Books) (32B) (54μs)
  • afterRenderRawModule mod_menu (Books) (26.94KB) (379μs)
  • beforeRenderModule mod_menu (Books) (704B) (5μs)
  • afterRenderModule mod_menu (Books) (12.18KB) (340μs)
  • beforeRenderRawModule mod_menu (Eklavya) (32B) (72μs)
  • afterRenderRawModule mod_menu (Eklavya) (53.14KB) (449μs)
  • beforeRenderModule mod_menu (Eklavya) (704B) (5μs)
  • afterRenderModule mod_menu (Eklavya) (12.05KB) (324μs)
  • beforeRenderRawModule mod_related_items (Related Articles) (1.89KB) (51μs)
  • afterRenderRawModule mod_related_items (Related Articles) (16.7KB) (952μs)
  • beforeRenderModule mod_related_items (Related Articles) (704B) (6μs)
  • afterRenderModule mod_related_items (Related Articles) (8.75KB) (312μs)
  • beforeRenderRawModule mod_articles_category (Articles) (7.7KB) (45μs)
  • Before Access::getAssetRules (id:8 name:com_content) (54.08KB) (2.73ms)
  • After Access::getAssetRules (id:8 name:com_content) (6.95KB) (61μs)
  • afterRenderRawModule mod_articles_category (Articles) (37.48KB) (13.78ms)
  • beforeRenderModule mod_articles_category (Articles) (704B) (9μs)
  • afterRenderModule mod_articles_category (Articles) (33.92KB) (602μs)
  • beforeRenderRawModule mod_search (Search module) (8.53KB) (72μs)
  • afterRenderRawModule mod_search (Search module) (2.59KB) (95μs)
  • beforeRenderModule mod_search (Search module) (720B) (4μs)
  • afterRenderModule mod_search (Search module) (1.26KB) (65μs)
  • beforeRenderRawModule mod_breadcrumbs (Breadcrumb) (2.41KB) (43μs)
  • afterRenderRawModule mod_breadcrumbs (Breadcrumb) (14.77KB) (915μs)
  • beforeRenderModule mod_breadcrumbs (Breadcrumb) (704B) (7μs)
  • afterRenderModule mod_breadcrumbs (Breadcrumb) (1.21KB) (110μs)
  • beforeRenderRawModule mod_menu (Search test Menu in content top) (1.95KB) (23μs)
  • afterRenderRawModule mod_menu (Search test Menu in content top) (15.65KB) (390μs)
  • beforeRenderModule mod_menu (Search test Menu in content top) (736B) (6μs)
  • afterRenderModule mod_menu (Search test Menu in content top) (12.23KB) (100μs)
  • beforeRenderRawModule mod_finder (search 22) (352B) (19μs)
  • afterRenderRawModule mod_finder (search 22) (241.79KB) (3.48ms)
  • beforeRenderModule mod_finder (search 22) (720B) (10μs)
  • afterRenderModule mod_finder (search 22) (1.23KB) (123μs)
  • beforeRenderRawModule mod_jfilters_filters (JFilters Filters) (672B) (24μs)
  • afterRenderRawModule mod_jfilters_filters (JFilters Filters) (253.09KB) (11.51ms)
  • beforeRenderModule mod_jfilters_filters (JFilters Filters) (736B) (9μs)
  • afterRenderModule mod_jfilters_filters (JFilters Filters) (1.23KB) (134μs)
  • beforeRenderRawModule mod_search (Search (Top)) (56B) (70μs)
  • afterRenderRawModule mod_search (Search (Top)) (944B) (30μs)
  • beforeRenderModule mod_search (Search (Top)) (720B) (3μs)
  • afterRenderModule mod_search (Search (Top)) (1.23KB) (64μs)
  • afterRender (367.45KB) (4.62ms)
  • 1 x beforeRenderRawModule mod_menu () (1.99MB) (23.46%)
    51.24ms
    1 x afterRenderComponent com_content (771.66KB) (13.11%)
    28.63ms
    1 x afterInitialise (1.31MB) (12.89%)
    28.15ms
    1 x afterRoute (3.17MB) (9.2%)
    20.09ms
    1 x After Access::preloadPermissions (com_content) (3.54MB) (7.6%)
    16.60ms
    1 x afterRenderRawModule mod_articles_category (Articles) (37.48KB) (6.31%)
    13.78ms
    1 x afterRenderRawModule mod_menu () (1.13MB) (5.54%)
    12.09ms
    1 x afterRenderRawModule mod_jfilters_filters (JFilters Filters) (253.09KB) (5.27%)
    11.51ms
    1 x afterRender (367.45KB) (2.12%)
    4.62ms
    1 x afterLoad (542.17KB) (1.66%)
    3.63ms
    1 x afterRenderRawModule mod_finder (search 22) (241.79KB) (1.59%)
    3.48ms
    1 x beforeRenderComponent com_content (73.16KB) (1.59%)
    3.47ms
    1 x After Access::preloadComponents (all components) (119.27KB) (1.34%)
    2.93ms
    1 x Before Access::getAssetRules (id:8 name:com_content) (54.08KB) (1.25%)
    2.73ms
    1 x afterRenderRawModule mod_menu () (26.45KB) (1.23%)
    2.68ms
    1 x afterRenderRawModule mod_related_items (Related Articles) (16.7KB) (0.44%)
    952μs
    1 x afterRenderRawModule mod_breadcrumbs (Breadcrumb) (14.77KB) (0.42%)
    915μs
    1 x Before Access::preloadComponents (all components) (34.2KB) (0.38%)
    836μs
    1 x beforeRenderRawModule mod_menu (More) (19.64KB) (0.31%)
    680μs
    1 x afterRenderModule mod_articles_category (Articles) (33.92KB) (0.28%)
    602μs
    1 x afterRenderModule mod_menu (More) (12.94KB) (0.22%)
    488μs
    1 x afterRenderRawModule mod_menu (More) (12.04KB) (0.22%)
    475μs
    1 x afterRenderRawModule mod_menu (Eklavya) (53.14KB) (0.21%)
    449μs
    1 x afterRenderModule mod_menu (Magazine) (12.3KB) (0.18%)
    397μs
    1 x afterRenderRawModule mod_menu (Search test Menu in content top) (15.65KB) (0.18%)
    390μs
    1 x afterRenderRawModule mod_menu (Books) (26.94KB) (0.17%)
    379μs
    1 x afterRenderModule mod_menu (Books) (12.18KB) (0.16%)
    340μs
    1 x afterRenderRawModule mod_menu (Gallery) (13.38KB) (0.15%)
    337μs
    1 x afterRenderModule mod_menu (Eklavya) (12.05KB) (0.15%)
    324μs
    1 x afterRenderModule mod_related_items (Related Articles) (8.75KB) (0.14%)
    312μs
    1 x afterRenderRawModule mod_menu (Magazine) (21.47KB) (0.12%)
    259μs
    1 x Before Access::getAssetRules (id:2851 name:com_content.article.2249) (258.8KB) (0.11%)
    236μs
    1 x afterDispatch (2.28KB) (0.09%)
    196μs
    1 x afterRenderModule mod_menu () (26.88KB) (0.08%)
    173μs
    1 x afterRenderModule mod_jfilters_filters (JFilters Filters) (1.23KB) (0.06%)
    134μs
    1 x afterRenderRawModule mod_menu () (65.22KB) (0.06%)
    128μs
    1 x After Access::getAssetRules (id:2851 name:com_content.article.2249) (8.47KB) (0.06%)
    127μs
    1 x afterRenderModule mod_finder (search 22) (1.23KB) (0.06%)
    123μs
    1 x afterRenderModule mod_menu () (26.27KB) (0.06%)
    122μs
    1 x afterRenderModule mod_breadcrumbs (Breadcrumb) (1.21KB) (0.05%)
    110μs
    1 x afterRenderModule mod_menu (Search test Menu in content top) (12.23KB) (0.05%)
    100μs
    1 x afterRenderRawModule mod_search (Search module) (2.59KB) (0.04%)
    95μs
    1 x afterRenderModule mod_menu (Gallery) (2.98KB) (0.04%)
    85μs
    1 x beforeRenderRawModule mod_menu (Gallery) (16B) (0.03%)
    73μs
    1 x beforeRenderRawModule mod_menu (Eklavya) (32B) (0.03%)
    72μs
    1 x beforeRenderRawModule mod_search (Search module) (8.53KB) (0.03%)
    72μs
    1 x beforeRenderRawModule mod_search (Search (Top)) (56B) (0.03%)
    70μs
    1 x afterRenderModule mod_search (Search module) (1.26KB) (0.03%)
    65μs
    1 x afterRenderModule mod_search (Search (Top)) (1.23KB) (0.03%)
    64μs
    1 x After Access::getAssetRules (id:8 name:com_content) (6.95KB) (0.03%)
    61μs
    1 x afterRenderModule mod_menu () (1.64KB) (0.03%)
    60μs
    1 x beforeRenderRawModule mod_menu (Books) (32B) (0.02%)
    54μs
    1 x beforeRenderRawModule mod_menu () (24.38KB) (0.02%)
    51μs
    1 x beforeRenderRawModule mod_related_items (Related Articles) (1.89KB) (0.02%)
    51μs
    1 x beforeRenderRawModule mod_menu (Magazine) (32B) (0.02%)
    45μs
    1 x beforeRenderRawModule mod_articles_category (Articles) (7.7KB) (0.02%)
    45μs
    1 x beforeRenderRawModule mod_breadcrumbs (Breadcrumb) (2.41KB) (0.02%)
    43μs
    1 x beforeRenderRawModule mod_menu () (24.48KB) (0.02%)
    40μs
    1 x Before Access::preloadPermissions (com_content) (4.16KB) (0.02%)
    36μs
    1 x afterRenderRawModule mod_search (Search (Top)) (944B) (0.01%)
    30μs
    3 x beforeRenderModule mod_menu () (696B) (0.01%)
    29μs
    1 x beforeRenderRawModule mod_jfilters_filters (JFilters Filters) (672B) (0.01%)
    24μs
    1 x beforeRenderRawModule mod_menu (Search test Menu in content top) (1.95KB) (0.01%)
    23μs
    1 x beforeRenderRawModule mod_finder (search 22) (352B) (0.01%)
    19μs
    1 x beforeRenderModule mod_finder (search 22) (720B) (0%)
    10μs
    1 x beforeRenderModule mod_menu (More) (704B) (0%)
    9μs
    1 x beforeRenderModule mod_articles_category (Articles) (704B) (0%)
    9μs
    1 x beforeRenderModule mod_jfilters_filters (JFilters Filters) (736B) (0%)
    9μs
    1 x beforeRenderModule mod_breadcrumbs (Breadcrumb) (704B) (0%)
    7μs
    1 x beforeRenderModule mod_menu (Gallery) (704B) (0%)
    6μs
    1 x beforeRenderModule mod_related_items (Related Articles) (704B) (0%)
    6μs
    1 x beforeRenderModule mod_menu (Search test Menu in content top) (736B) (0%)
    6μs
    1 x beforeRenderModule mod_menu (Books) (704B) (0%)
    5μs
    1 x beforeRenderModule mod_menu (Eklavya) (704B) (0%)
    5μs
    1 x beforeRenderModule mod_menu (Magazine) (704B) (0%)
    4μs
    1 x beforeRenderModule mod_search (Search module) (720B) (0%)
    4μs
    1 x beforeRenderModule mod_search (Search (Top)) (720B) (0%)
    3μs
143 statements were executed, 3 of which were duplicates, 140 unique69.03ms3.68MB
UniquesDuplicates 1
  • SELECT @@SESSION.sql_mode;142μs1.57KB/libraries/vendor/joomla/database/src/Mysqli/MysqliDriver.php:334Copy
  • SELECT `data` FROM `j4_session` WHERE `session_id` = ?178μs1.61KBParams/libraries/vendor/joomla/session/src/Handler/DatabaseHandler.php:261Copy
  • SELECT `session_id` FROM `j4_session` WHERE `session_id` = :session_id LIMIT 1136μs1.61KBParams/libraries/src/Session/MetadataManager.php:187Copy
  • INSERT INTO `j4_session` (`session_id`,`guest`,`time`,`userid`,`username`,`client_id`) VALUES (:session_id, :guest, :time, :user_id, :username, :client_id)217μs944BParams/libraries/src/Session/MetadataManager.php:260Copy
  • SELECT `extension_id` AS `id`,`element` AS `option`,`params`,`enabled` FROM `j4_extensions` WHERE `type` = 'component' AND `state` = 0 AND `enabled` = 1551μs2.36KB/libraries/src/Component/ComponentHelper.php:399Copy
  • SELECT `id`,`rules` FROM `j4_viewlevels`201μs976B/libraries/src/Access/Access.php:955Copy
  • SELECT `b`.`id` FROM `j4_usergroups` AS `a` LEFT JOIN `j4_usergroups` AS `b` ON `b`.`lft` <= `a`.`lft` AND `b`.`rgt` >= `a`.`rgt` WHERE `a`.`id` = :guest270μs1.63KBParams/libraries/src/Access/Access.php:868Copy
  • SELECT `folder` AS `type`,`element` AS `name`,`params` AS `params`,`extension_id` AS `id` FROM `j4_extensions` WHERE `enabled` = 1 AND `type` = 'plugin' AND `state` IN (0,1) AND `access` IN (:preparedArray1) ORDER BY `ordering`3.41ms4.27KBParams/libraries/src/Plugin/PluginHelper.php:294Copy
  • SELECT * FROM j4_rsform_config200μs2.56KB/administrator/components/com_rsform/helpers/config.php:52Copy
  • SELECT `m`.`id`,`m`.`menutype`,`m`.`title`,`m`.`alias`,`m`.`note`,`m`.`link`,`m`.`type`,`m`.`level`,`m`.`language`,`m`.`browserNav`,`m`.`access`,`m`.`params`,`m`.`home`,`m`.`img`,`m`.`template_style_id`,`m`.`component_id`,`m`.`parent_id`,`m`.`path` AS `route`,`e`.`element` AS `component` FROM `j4_menu` AS `m` LEFT JOIN `j4_extensions` AS `e` ON `m`.`component_id` = `e`.`extension_id` WHERE ( (`m`.`published` = 1 AND `m`.`parent_id` > 0 AND `m`.`client_id` = 0) AND (`m`.`publish_up` IS NULL OR `m`.`publish_up` <= :currentDate1)) AND (`m`.`publish_down` IS NULL OR `m`.`publish_down` >= :currentDate2) ORDER BY `m`.`lft`2.24ms167.05KBParams/libraries/src/Menu/SiteMenu.php:166Copy
  • SELECT `c`.`id`,`c`.`asset_id`,`c`.`access`,`c`.`alias`,`c`.`checked_out`,`c`.`checked_out_time`,`c`.`created_time`,`c`.`created_user_id`,`c`.`description`,`c`.`extension`,`c`.`hits`,`c`.`language`,`c`.`level`,`c`.`lft`,`c`.`metadata`,`c`.`metadesc`,`c`.`metakey`,`c`.`modified_time`,`c`.`note`,`c`.`params`,`c`.`parent_id`,`c`.`path`,`c`.`published`,`c`.`rgt`,`c`.`title`,`c`.`modified_user_id`,`c`.`version`, CASE WHEN CHAR_LENGTH(`c`.`alias`) != 0 THEN CONCAT_WS(':', `c`.`id`, `c`.`alias`) ELSE `c`.`id` END as `slug` FROM `j4_categories` AS `s` INNER JOIN `j4_categories` AS `c` ON (`s`.`lft` <= `c`.`lft` AND `c`.`lft` < `s`.`rgt`) OR (`c`.`lft` < `s`.`lft` AND `s`.`rgt` < `c`.`rgt`) WHERE (`c`.`extension` = :extension OR `c`.`extension` = 'system') AND `c`.`published` = 1 AND `s`.`id` = :id ORDER BY `c`.`lft`7.16ms2.15MBParams/libraries/src/Categories/Categories.php:375Copy
  • SELECT * FROM `j4_languages` WHERE `published` = 1 ORDER BY `ordering` ASC314μs2.22KB/libraries/src/Language/LanguageHelper.php:142Copy
  • SELECT `id`,`home`,`template`,`s`.`params`,`inheritable`,`parent` FROM `j4_template_styles` AS `s` LEFT JOIN `j4_extensions` AS `e` ON `e`.`element` = `s`.`template` AND `e`.`type` = 'template' AND `e`.`client_id` = `s`.`client_id` WHERE `s`.`client_id` = 0 AND `e`.`enabled` = 1518μs1.14KB/administrator/components/com_templates/src/Model/StyleModel.php:773Copy
  • SELECT `id`,`name`,`rules`,`parent_id` FROM `j4_assets` WHERE `name` IN (:preparedArray1,:preparedArray2,:preparedArray3,:preparedArray4,:preparedArray5,:preparedArray6,:preparedArray7,:preparedArray8,:preparedArray9,:preparedArray10,:preparedArray11,:preparedArray12,:preparedArray13,:preparedArray14,:preparedArray15,:preparedArray16,:preparedArray17,:preparedArray18,:preparedArray19,:preparedArray20,:preparedArray21,:preparedArray22,:preparedArray23,:preparedArray24,:preparedArray25,:preparedArray26,:preparedArray27,:preparedArray28,:preparedArray29,:preparedArray30,:preparedArray31,:preparedArray32,:preparedArray33,:preparedArray34,:preparedArray35,:preparedArray36,:preparedArray37,:preparedArray38,:preparedArray39,:preparedArray40,:preparedArray41,:preparedArray42,:preparedArray43,:preparedArray44,:preparedArray45,:preparedArray46,:preparedArray47)2.17ms8.12KBParams/libraries/src/Access/Access.php:357Copy
  • SELECT `id`,`name`,`rules`,`parent_id` FROM `j4_assets` WHERE `name` LIKE :asset OR `name` = :extension OR `parent_id` = 07.73ms345.8KBParams/libraries/src/Access/Access.php:301Copy
  • SHOW FULL COLUMNS FROM `j4_content`1.17ms2.39KB/libraries/vendor/joomla/database/src/Mysqli/MysqliDriver.php:625Copy
  • UPDATE `j4_content` SET `hits` = (`hits` + 1) WHERE `id` = '2249'1.65ms2.55KB/libraries/src/Table/Table.php:1325Copy
  • SELECT `a`.`id`,`a`.`asset_id`,`a`.`title`,`a`.`alias`,`a`.`introtext`,`a`.`fulltext`,`a`.`state`,`a`.`catid`,`a`.`created`,`a`.`created_by`,`a`.`created_by_alias`,`a`.`modified`,`a`.`modified_by`,`a`.`checked_out`,`a`.`checked_out_time`,`a`.`publish_up`,`a`.`publish_down`,`a`.`images`,`a`.`urls`,`a`.`attribs`,`a`.`version`,`a`.`ordering`,`a`.`metakey`,`a`.`metadesc`,`a`.`access`,`a`.`hits`,`a`.`metadata`,`a`.`featured`,`a`.`language`,`fp`.`featured_up`,`fp`.`featured_down`,`c`.`title` AS `category_title`,`c`.`alias` AS `category_alias`,`c`.`access` AS `category_access`,`c`.`language` AS `category_language`,`fp`.`ordering`,`u`.`name` AS `author`,`parent`.`title` AS `parent_title`,`parent`.`id` AS `parent_id`,`parent`.`path` AS `parent_route`,`parent`.`alias` AS `parent_alias`,`parent`.`language` AS `parent_language`,ROUND(`v`.`rating_sum` / `v`.`rating_count`, 1) AS `rating`,`v`.`rating_count` AS `rating_count` FROM `j4_content` AS `a` INNER JOIN `j4_categories` AS `c` ON `c`.`id` = `a`.`catid` LEFT JOIN `j4_content_frontpage` AS `fp` ON `fp`.`content_id` = `a`.`id` LEFT JOIN `j4_users` AS `u` ON `u`.`id` = `a`.`created_by` LEFT JOIN `j4_categories` AS `parent` ON `parent`.`id` = `c`.`parent_id` LEFT JOIN `j4_content_rating` AS `v` ON `a`.`id` = `v`.`content_id` WHERE ( (`a`.`id` = :pk AND `c`.`published` > 0) AND (`a`.`publish_up` IS NULL OR `a`.`publish_up` <= :publishUp)) AND (`a`.`publish_down` IS NULL OR `a`.`publish_down` >= :publishDown) AND `a`.`state` IN (:preparedArray1,:preparedArray2)1.41ms120.63KBParams/components/com_content/src/Model/ArticleModel.php:215Copy
  • SELECT `c`.`id`,`c`.`asset_id`,`c`.`access`,`c`.`alias`,`c`.`checked_out`,`c`.`checked_out_time`,`c`.`created_time`,`c`.`created_user_id`,`c`.`description`,`c`.`extension`,`c`.`hits`,`c`.`language`,`c`.`level`,`c`.`lft`,`c`.`metadata`,`c`.`metadesc`,`c`.`metakey`,`c`.`modified_time`,`c`.`note`,`c`.`params`,`c`.`parent_id`,`c`.`path`,`c`.`published`,`c`.`rgt`,`c`.`title`,`c`.`modified_user_id`,`c`.`version`, CASE WHEN CHAR_LENGTH(`c`.`alias`) != 0 THEN CONCAT_WS(':', `c`.`id`, `c`.`alias`) ELSE `c`.`id` END as `slug` FROM `j4_categories` AS `s` INNER JOIN `j4_categories` AS `c` ON (`s`.`lft` <= `c`.`lft` AND `c`.`lft` < `s`.`rgt`) OR (`c`.`lft` < `s`.`lft` AND `s`.`rgt` < `c`.`rgt`) WHERE (`c`.`extension` = :extension OR `c`.`extension` = 'system') AND `c`.`access` IN (:preparedArray1) AND `c`.`published` = 1 AND `s`.`id` = :id ORDER BY `c`.`lft`2.92ms21.19KBParams/libraries/src/Categories/Categories.php:375Copy
  • SELECT `m`.`tag_id`,`t`.* FROM `j4_contentitem_tag_map` AS `m` INNER JOIN `j4_tags` AS `t` ON `m`.`tag_id` = `t`.`id` WHERE `m`.`type_alias` = :contentType AND `m`.`content_item_id` = :id AND `t`.`published` = 1 AND `t`.`access` IN (:preparedArray1)396μs5.2KBParams/libraries/src/Helper/TagsHelper.php:388Copy
  • SELECT `c`.`id`,`c`.`asset_id`,`c`.`access`,`c`.`alias`,`c`.`checked_out`,`c`.`checked_out_time`,`c`.`created_time`,`c`.`created_user_id`,`c`.`description`,`c`.`extension`,`c`.`hits`,`c`.`language`,`c`.`level`,`c`.`lft`,`c`.`metadata`,`c`.`metadesc`,`c`.`metakey`,`c`.`modified_time`,`c`.`note`,`c`.`params`,`c`.`parent_id`,`c`.`path`,`c`.`published`,`c`.`rgt`,`c`.`title`,`c`.`modified_user_id`,`c`.`version`, CASE WHEN CHAR_LENGTH(`c`.`alias`) != 0 THEN CONCAT_WS(':', `c`.`id`, `c`.`alias`) ELSE `c`.`id` END as `slug` FROM `j4_categories` AS `s` INNER JOIN `j4_categories` AS `c` ON (`s`.`lft` <= `c`.`lft` AND `c`.`lft` < `s`.`rgt`) OR (`c`.`lft` < `s`.`lft` AND `s`.`rgt` < `c`.`rgt`) WHERE (`c`.`extension` = :extension OR `c`.`extension` = 'system') AND `c`.`access` IN (:preparedArray1) AND `c`.`published` = 1 AND `s`.`id` = :id ORDER BY `c`.`lft`3.35ms21.19KBParams/libraries/src/Categories/Categories.php:375Copy
  • SELECT DISTINCT a.id, a.title, a.name, a.checked_out, a.checked_out_time, a.note, a.state, a.access, a.created_time, a.created_user_id, a.ordering, a.language, a.fieldparams, a.params, a.type, a.default_value, a.context, a.group_id, a.label, a.description, a.required, a.only_use_in_subform,l.title AS language_title, l.image AS language_image,uc.name AS editor,ag.title AS access_level,ua.name AS author_name,g.title AS group_title, g.access as group_access, g.state AS group_state, g.note as group_note FROM j4_fields AS a LEFT JOIN `j4_languages` AS l ON l.lang_code = a.language LEFT JOIN j4_users AS uc ON uc.id=a.checked_out LEFT JOIN j4_viewlevels AS ag ON ag.id = a.access LEFT JOIN j4_users AS ua ON ua.id = a.created_user_id LEFT JOIN j4_fields_groups AS g ON g.id = a.group_id LEFT JOIN `j4_fields_categories` AS fc ON fc.field_id = a.id WHERE ( (`a`.`context` = :context AND (`fc`.`category_id` IS NULL OR `fc`.`category_id` IN (:preparedArray1,:preparedArray2,:preparedArray3,:preparedArray4,:preparedArray5)) AND `a`.`access` IN (:preparedArray6)) AND (`a`.`group_id` = 0 OR `g`.`access` IN (:preparedArray7)) AND `a`.`state` = :state) AND (`a`.`group_id` = 0 OR `g`.`state` = :gstate) AND `a`.`only_use_in_subform` = :only_use_in_subform ORDER BY a.ordering ASC728μs6.06KBParams/libraries/src/MVC/Model/BaseDatabaseModel.php:166Copy
  • SELECT `c`.`id`,`c`.`asset_id`,`c`.`access`,`c`.`alias`,`c`.`checked_out`,`c`.`checked_out_time`,`c`.`created_time`,`c`.`created_user_id`,`c`.`description`,`c`.`extension`,`c`.`hits`,`c`.`language`,`c`.`level`,`c`.`lft`,`c`.`metadata`,`c`.`metadesc`,`c`.`metakey`,`c`.`modified_time`,`c`.`note`,`c`.`params`,`c`.`parent_id`,`c`.`path`,`c`.`published`,`c`.`rgt`,`c`.`title`,`c`.`modified_user_id`,`c`.`version`, CASE WHEN CHAR_LENGTH(`c`.`alias`) != 0 THEN CONCAT_WS(':', `c`.`id`, `c`.`alias`) ELSE `c`.`id` END as `slug` FROM `j4_categories` AS `s` INNER JOIN `j4_categories` AS `c` ON (`s`.`lft` <= `c`.`lft` AND `c`.`lft` < `s`.`rgt`) OR (`c`.`lft` < `s`.`lft` AND `s`.`rgt` < `c`.`rgt`) WHERE (`c`.`extension` = :extension OR `c`.`extension` = 'system') AND `c`.`access` IN (:preparedArray1) AND `c`.`published` = 1 AND `s`.`id` = :id ORDER BY `c`.`lft`3.06ms21.19KBParams/libraries/src/Categories/Categories.php:375Copy
  • SELECT m.id, m.title, m.module, m.position, m.content, m.showtitle, m.params,am.params AS extra, 0 AS menuid, m.publish_up, m.publish_down FROM j4_modules AS m LEFT JOIN j4_extensions AS e ON e.element = m.module AND e.client_id = m.client_id LEFT JOIN j4_advancedmodules as am ON am.module_id = m.id WHERE m.published = 1 AND e.enabled = 1 AND m.client_id = 0 ORDER BY m.position, m.ordering690μs50.67KB/plugins/system/advancedmodules/src/Helper.php:191Copy
  • SELECT m.condition_id,m.item_id FROM j4_conditions_map as m LEFT JOIN j4_conditions as c ON c.id = m.condition_id WHERE `m`.`extension` = 'com_advancedmodules' AND `c`.`published` = 1323μs1.75KB/administrator/components/com_conditions/src/Model/ItemModel.php:821Copy
  • SHOW FULL COLUMNS FROM `j4_conditions`806μs2.08KB/libraries/vendor/joomla/database/src/Mysqli/MysqliDriver.php:625Copy
  • SELECT * FROM `j4_conditions` WHERE `id` = '14'160μs2.06KB/libraries/src/Table/Table.php:755Copy
  • SELECT * FROM j4_conditions_groups as g WHERE g.condition_id = 14132μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:1034Copy
  • SELECT * FROM j4_conditions_rules as r WHERE r.group_id = 14128μs1.13KB/administrator/components/com_conditions/src/Model/GroupModel.php:108Copy
  • SELECT m.extension,m.item_id,m.table,m.name_column FROM j4_conditions_map as m WHERE m.condition_id = 14 ORDER BY m.extension,m.item_id119μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:907Copy
  • SELECT `id`,`title` AS `value` FROM `j4_modules`162μs3.38KB/administrator/components/com_conditions/src/Helper/Helper.php:184Copy
  • SHOW FULL COLUMNS FROM `j4_modules`841μs2.2KB/libraries/vendor/joomla/database/src/Mysqli/MysqliDriver.php:625Copy
  • SELECT `id`,`published` AS `value` FROM `j4_modules`218μs14.38KB/administrator/components/com_conditions/src/Helper/Helper.php:184Copy
  • SELECT * FROM `j4_conditions` WHERE `id` = '15'148μs2.06KB/libraries/src/Table/Table.php:755Copy
  • SELECT * FROM j4_conditions_groups as g WHERE g.condition_id = 15131μs1008B/administrator/components/com_conditions/src/Model/ItemModel.php:1034Copy
  • SELECT m.extension,m.item_id,m.table,m.name_column FROM j4_conditions_map as m WHERE m.condition_id = 15 ORDER BY m.extension,m.item_id129μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:907Copy
  • SELECT * FROM `j4_conditions` WHERE `id` = '16'126μs2.06KB/libraries/src/Table/Table.php:755Copy
  • SELECT * FROM j4_conditions_groups as g WHERE g.condition_id = 16101μs1008B/administrator/components/com_conditions/src/Model/ItemModel.php:1034Copy
  • SELECT m.extension,m.item_id,m.table,m.name_column FROM j4_conditions_map as m WHERE m.condition_id = 16 ORDER BY m.extension,m.item_id121μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:907Copy
  • SELECT * FROM `j4_conditions` WHERE `id` = '18'105μs2.06KB/libraries/src/Table/Table.php:755Copy
  • SELECT * FROM j4_conditions_groups as g WHERE g.condition_id = 1893μs1008B/administrator/components/com_conditions/src/Model/ItemModel.php:1034Copy
  • SELECT m.extension,m.item_id,m.table,m.name_column FROM j4_conditions_map as m WHERE m.condition_id = 18 ORDER BY m.extension,m.item_id103μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:907Copy
  • SELECT * FROM `j4_conditions` WHERE `id` = '23'113μs2.06KB/libraries/src/Table/Table.php:755Copy
  • SELECT * FROM j4_conditions_groups as g WHERE g.condition_id = 23106μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:1034Copy
  • SELECT * FROM j4_conditions_rules as r WHERE r.group_id = 1999μs1.13KB/administrator/components/com_conditions/src/Model/GroupModel.php:108Copy
  • SELECT m.extension,m.item_id,m.table,m.name_column FROM j4_conditions_map as m WHERE m.condition_id = 23 ORDER BY m.extension,m.item_id104μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:907Copy
  • SELECT * FROM `j4_conditions` WHERE `id` = '24'114μs2.06KB/libraries/src/Table/Table.php:755Copy
  • SELECT * FROM j4_conditions_groups as g WHERE g.condition_id = 24103μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:1034Copy
  • SELECT * FROM j4_conditions_rules as r WHERE r.group_id = 20123μs1.13KB/administrator/components/com_conditions/src/Model/GroupModel.php:108Copy
  • SELECT m.extension,m.item_id,m.table,m.name_column FROM j4_conditions_map as m WHERE m.condition_id = 24 ORDER BY m.extension,m.item_id117μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:907Copy
  • SELECT * FROM `j4_conditions` WHERE `id` = '25'102μs2.06KB/libraries/src/Table/Table.php:755Copy
  • SELECT * FROM j4_conditions_groups as g WHERE g.condition_id = 25114μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:1034Copy
  • SELECT * FROM j4_conditions_rules as r WHERE r.group_id = 2199μs1.13KB/administrator/components/com_conditions/src/Model/GroupModel.php:108Copy
  • SELECT m.extension,m.item_id,m.table,m.name_column FROM j4_conditions_map as m WHERE m.condition_id = 25 ORDER BY m.extension,m.item_id142μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:907Copy
  • SELECT * FROM `j4_conditions` WHERE `id` = '53'119μs2.06KB/libraries/src/Table/Table.php:755Copy
  • SELECT * FROM j4_conditions_groups as g WHERE g.condition_id = 53105μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:1034Copy
  • SELECT * FROM j4_conditions_rules as r WHERE r.group_id = 45100μs1.13KB/administrator/components/com_conditions/src/Model/GroupModel.php:108Copy
  • SELECT m.extension,m.item_id,m.table,m.name_column FROM j4_conditions_map as m WHERE m.condition_id = 53 ORDER BY m.extension,m.item_id103μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:907Copy
  • SELECT * FROM `j4_conditions` WHERE `id` = '29'103μs2.06KB/libraries/src/Table/Table.php:755Copy
  • SELECT * FROM j4_conditions_groups as g WHERE g.condition_id = 29116μs1008B/administrator/components/com_conditions/src/Model/ItemModel.php:1034Copy
  • SELECT m.extension,m.item_id,m.table,m.name_column FROM j4_conditions_map as m WHERE m.condition_id = 29 ORDER BY m.extension,m.item_id128μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:907Copy
  • SELECT * FROM `j4_conditions` WHERE `id` = '31'101μs2.06KB/libraries/src/Table/Table.php:755Copy
  • SELECT * FROM j4_conditions_groups as g WHERE g.condition_id = 31101μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:1034Copy
  • SELECT * FROM j4_conditions_rules as r WHERE r.group_id = 4399μs1.13KB/administrator/components/com_conditions/src/Model/GroupModel.php:108Copy
  • SELECT m.extension,m.item_id,m.table,m.name_column FROM j4_conditions_map as m WHERE m.condition_id = 31 ORDER BY m.extension,m.item_id116μs9.02KB/administrator/components/com_conditions/src/Model/ItemModel.php:907Copy
  • SELECT * FROM `j4_conditions` WHERE `id` = '36'100μs2.06KB/libraries/src/Table/Table.php:755Copy
  • SELECT * FROM j4_conditions_groups as g WHERE g.condition_id = 36115μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:1034Copy
  • SELECT * FROM j4_conditions_rules as r WHERE r.group_id = 31101μs1.14KB/administrator/components/com_conditions/src/Model/GroupModel.php:108Copy
  • SELECT m.extension,m.item_id,m.table,m.name_column FROM j4_conditions_map as m WHERE m.condition_id = 36 ORDER BY m.extension,m.item_id117μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:907Copy
  • SELECT * FROM `j4_conditions` WHERE `id` = '10'117μs2.06KB/libraries/src/Table/Table.php:755Copy
  • SELECT * FROM j4_conditions_groups as g WHERE g.condition_id = 10101μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:1034Copy
  • SELECT * FROM j4_conditions_rules as r WHERE r.group_id = 10102μs1.14KB/administrator/components/com_conditions/src/Model/GroupModel.php:108Copy
  • SELECT m.extension,m.item_id,m.table,m.name_column FROM j4_conditions_map as m WHERE m.condition_id = 10 ORDER BY m.extension,m.item_id105μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:907Copy
  • SELECT * FROM `j4_conditions` WHERE `id` = '37'103μs2.06KB/libraries/src/Table/Table.php:755Copy
  • SELECT * FROM j4_conditions_groups as g WHERE g.condition_id = 37100μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:1034Copy
  • SELECT * FROM j4_conditions_rules as r WHERE r.group_id = 32101μs1.14KB/administrator/components/com_conditions/src/Model/GroupModel.php:108Copy
  • SELECT m.extension,m.item_id,m.table,m.name_column FROM j4_conditions_map as m WHERE m.condition_id = 37 ORDER BY m.extension,m.item_id118μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:907Copy
  • SELECT * FROM `j4_conditions` WHERE `id` = '35'116μs2.06KB/libraries/src/Table/Table.php:755Copy
  • SELECT * FROM j4_conditions_groups as g WHERE g.condition_id = 35120μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:1034Copy
  • SELECT * FROM j4_conditions_rules as r WHERE r.group_id = 30108μs1.14KB/administrator/components/com_conditions/src/Model/GroupModel.php:108Copy
  • SELECT m.extension,m.item_id,m.table,m.name_column FROM j4_conditions_map as m WHERE m.condition_id = 35 ORDER BY m.extension,m.item_id120μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:907Copy
  • SELECT * FROM `j4_conditions` WHERE `id` = '51'118μs2.06KB/libraries/src/Table/Table.php:755Copy
  • SELECT * FROM j4_conditions_groups as g WHERE g.condition_id = 51110μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:1034Copy
  • SELECT * FROM j4_conditions_rules as r WHERE r.group_id = 41104μs1.16KB/administrator/components/com_conditions/src/Model/GroupModel.php:108Copy
  • SELECT m.extension,m.item_id,m.table,m.name_column FROM j4_conditions_map as m WHERE m.condition_id = 51 ORDER BY m.extension,m.item_id118μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:907Copy
  • SELECT * FROM `j4_conditions` WHERE `id` = '54'109μs2.06KB/libraries/src/Table/Table.php:755Copy
  • SELECT * FROM j4_conditions_groups as g WHERE g.condition_id = 54129μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:1034Copy
  • SELECT * FROM j4_conditions_rules as r WHERE r.group_id = 46173μs1.13KB/administrator/components/com_conditions/src/Model/GroupModel.php:108Copy
  • SELECT m.extension,m.item_id,m.table,m.name_column FROM j4_conditions_map as m WHERE m.condition_id = 54 ORDER BY m.extension,m.item_id110μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:907Copy
  • SELECT * FROM `j4_conditions` WHERE `id` = '7'107μs2.06KB/libraries/src/Table/Table.php:755Copy
  • SELECT * FROM j4_conditions_groups as g WHERE g.condition_id = 7102μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:1034Copy
  • SELECT * FROM j4_conditions_rules as r WHERE r.group_id = 7100μs1.14KB/administrator/components/com_conditions/src/Model/GroupModel.php:108Copy
  • SELECT m.extension,m.item_id,m.table,m.name_column FROM j4_conditions_map as m WHERE m.condition_id = 7 ORDER BY m.extension,m.item_id105μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:907Copy
  • SELECT * FROM `j4_conditions` WHERE `id` = '45'111μs2.06KB/libraries/src/Table/Table.php:755Copy
  • SELECT * FROM j4_conditions_groups as g WHERE g.condition_id = 45164μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:1034Copy
  • SELECT * FROM j4_conditions_rules as r WHERE r.group_id = 39123μs1.16KB/administrator/components/com_conditions/src/Model/GroupModel.php:108Copy
  • SELECT m.extension,m.item_id,m.table,m.name_column FROM j4_conditions_map as m WHERE m.condition_id = 45 ORDER BY m.extension,m.item_id119μs1.11KB/administrator/components/com_conditions/src/Model/ItemModel.php:907Copy
  • SELECT * FROM `j4_conditions` WHERE `id` = '50'112μs2.06KB/libraries/src/Table/Table.php:755Copy
  • SELECT * FROM j4_conditions_groups as g WHERE g.condition_id = 50105μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:1034Copy
  • SELECT * FROM j4_conditions_rules as r WHERE r.group_id = 40117μs1.16KB/administrator/components/com_conditions/src/Model/GroupModel.php:108Copy
  • SELECT m.extension,m.item_id,m.table,m.name_column FROM j4_conditions_map as m WHERE m.condition_id = 50 ORDER BY m.extension,m.item_id134μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:907Copy
  • SELECT * FROM `j4_conditions` WHERE `id` = '11'119μs2.06KB/libraries/src/Table/Table.php:755Copy
  • SELECT * FROM j4_conditions_groups as g WHERE g.condition_id = 11125μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:1034Copy
  • SELECT * FROM j4_conditions_rules as r WHERE r.group_id = 11100μs1.13KB/administrator/components/com_conditions/src/Model/GroupModel.php:108Copy
  • SELECT m.extension,m.item_id,m.table,m.name_column FROM j4_conditions_map as m WHERE m.condition_id = 11 ORDER BY m.extension,m.item_id130μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:907Copy
  • SELECT * FROM `j4_conditions` WHERE `id` = '30'121μs2.06KB/libraries/src/Table/Table.php:755Copy
  • SELECT * FROM j4_conditions_groups as g WHERE g.condition_id = 30119μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:1034Copy
  • SELECT * FROM j4_conditions_rules as r WHERE r.group_id = 25103μs1.13KB/administrator/components/com_conditions/src/Model/GroupModel.php:108Copy
  • SELECT m.extension,m.item_id,m.table,m.name_column FROM j4_conditions_map as m WHERE m.condition_id = 30 ORDER BY m.extension,m.item_id122μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:907Copy
  • SELECT * FROM `j4_conditions` WHERE `id` = '5'114μs2.06KB/libraries/src/Table/Table.php:755Copy
  • SELECT * FROM j4_conditions_groups as g WHERE g.condition_id = 5115μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:1034Copy
  • SELECT * FROM j4_conditions_rules as r WHERE r.group_id = 5183μs1.13KB/administrator/components/com_conditions/src/Model/GroupModel.php:108Copy
  • SELECT m.extension,m.item_id,m.table,m.name_column FROM j4_conditions_map as m WHERE m.condition_id = 5 ORDER BY m.extension,m.item_id120μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:907Copy
  • SELECT * FROM `j4_conditions` WHERE `id` = '52'138μs2.06KB/libraries/src/Table/Table.php:755Copy
  • SELECT * FROM j4_conditions_groups as g WHERE g.condition_id = 52109μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:1034Copy
  • SELECT * FROM j4_conditions_rules as r WHERE r.group_id = 42103μs1.13KB/administrator/components/com_conditions/src/Model/GroupModel.php:108Copy
  • SELECT m.extension,m.item_id,m.table,m.name_column FROM j4_conditions_map as m WHERE m.condition_id = 52 ORDER BY m.extension,m.item_id123μs1.02KB/administrator/components/com_conditions/src/Model/ItemModel.php:907Copy
  • SELECT * FROM `j4_conditions` WHERE `id` = '4'105μs2.06KB/libraries/src/Table/Table.php:755Copy
  • SELECT * FROM j4_conditions_groups as g WHERE g.condition_id = 4104μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:1034Copy
  • SELECT * FROM j4_conditions_rules as r WHERE r.group_id = 4100μs1.13KB/administrator/components/com_conditions/src/Model/GroupModel.php:108Copy
  • SELECT m.extension,m.item_id,m.table,m.name_column FROM j4_conditions_map as m WHERE m.condition_id = 4 ORDER BY m.extension,m.item_id147μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:907Copy
  • SELECT * FROM `j4_conditions` WHERE `id` = '1'144μs2.06KB/libraries/src/Table/Table.php:755Copy
  • SELECT * FROM j4_conditions_groups as g WHERE g.condition_id = 1169μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:1034Copy
  • SELECT * FROM j4_conditions_rules as r WHERE r.group_id = 1208μs1.14KB/administrator/components/com_conditions/src/Model/GroupModel.php:108Copy
  • SELECT m.extension,m.item_id,m.table,m.name_column FROM j4_conditions_map as m WHERE m.condition_id = 1 ORDER BY m.extension,m.item_id181μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:907Copy
  • SELECT * FROM `j4_conditions` WHERE `id` = '2'230μs2.06KB/libraries/src/Table/Table.php:755Copy
  • SELECT * FROM j4_conditions_groups as g WHERE g.condition_id = 2166μs1KB/administrator/components/com_conditions/src/Model/ItemModel.php:1034Copy
  • SELECT * FROM j4_conditions_rules as r WHERE r.group_id = 2180μs1.14KB/administrator/components/com_conditions/src/Model/GroupModel.php:108Copy
  • SELECT m.extension,m.item_id,m.table,m.name_column FROM j4_conditions_map as m WHERE m.condition_id = 2 ORDER BY m.extension,m.item_id184μs17KB/administrator/components/com_conditions/src/Model/ItemModel.php:907Copy
  • SELECT a.params FROM j4_advancedmodules AS a WHERE a.module_id = 19183μs840B/plugins/system/advancedmodules/src/Helper.php:151Copy
  • SELECT a.params FROM j4_advancedmodules AS a WHERE a.module_id = 189111μs840B/plugins/system/advancedmodules/src/Helper.php:151Copy
  • SELECT a.params FROM j4_advancedmodules AS a WHERE a.module_id = 18877μs840B/plugins/system/advancedmodules/src/Helper.php:151Copy
  • SELECT a.params FROM j4_advancedmodules AS a WHERE a.module_id = 18576μs840B/plugins/system/advancedmodules/src/Helper.php:151Copy
  • SELECT `metakey` FROM `j4_content` WHERE `id` = :id145μs1.63KBParams/modules/mod_related_items/src/Helper/RelatedItemsHelper.php:88Copy
  • SELECT a.params FROM j4_advancedmodules AS a WHERE a.module_id = 22385μs840B/plugins/system/advancedmodules/src/Helper.php:151Copy
  • SELECT `a`.`id`,`a`.`title`,`a`.`alias`,`a`.`introtext`,`a`.`fulltext`,`a`.`checked_out`,`a`.`checked_out_time`,`a`.`catid`,`a`.`created`,`a`.`created_by`,`a`.`created_by_alias`,`a`.`modified`,`a`.`modified_by`,CASE WHEN `a`.`publish_up` IS NULL THEN `a`.`created` ELSE `a`.`publish_up` END AS `publish_up`,`a`.`publish_down`,`a`.`images`,`a`.`urls`,`a`.`attribs`,`a`.`metadata`,`a`.`metakey`,`a`.`metadesc`,`a`.`access`,`a`.`hits`,`a`.`featured`,`a`.`language`,LENGTH(`a`.`fulltext`) AS `readmore`,`a`.`ordering`,`fp`.`featured_up`,`fp`.`featured_down`,CASE WHEN `c`.`published` = 2 AND `a`.`state` > 0 THEN 2 WHEN `c`.`published` != 1 THEN 0 ELSE `a`.`state` END AS `state`,`c`.`title` AS `category_title`,`c`.`path` AS `category_route`,`c`.`access` AS `category_access`,`c`.`alias` AS `category_alias`,`c`.`language` AS `category_language`,`c`.`published`,`c`.`published` AS `parents_published`,`c`.`lft`,CASE WHEN `a`.`created_by_alias` > ' ' THEN `a`.`created_by_alias` ELSE `ua`.`name` END AS `author`,`ua`.`email` AS `author_email`,`uam`.`name` AS `modified_by_name`,`parent`.`title` AS `parent_title`,`parent`.`id` AS `parent_id`,`parent`.`path` AS `parent_route`,`parent`.`alias` AS `parent_alias`,`parent`.`language` AS `parent_language`,COALESCE(NULLIF(ROUND(`v`.`rating_sum` / `v`.`rating_count`, 1), 0), 0) AS `rating`,COALESCE(NULLIF(`v`.`rating_count`, 0), 0) AS `rating_count` FROM `j4_content` AS `a` LEFT JOIN `j4_categories` AS `c` ON `c`.`id` = `a`.`catid` LEFT JOIN `j4_users` AS `ua` ON `ua`.`id` = `a`.`created_by` LEFT JOIN `j4_users` AS `uam` ON `uam`.`id` = `a`.`modified_by` LEFT JOIN `j4_categories` AS `parent` ON `parent`.`id` = `c`.`parent_id` LEFT JOIN `j4_content_frontpage` AS `fp` ON `fp`.`content_id` = `a`.`id` LEFT JOIN `j4_content_rating` AS `v` ON `a`.`id` = `v`.`content_id` WHERE `a`.`access` IN (:preparedArray1) AND `c`.`access` IN (:preparedArray2) AND `c`.`published` = 1 AND `a`.`state` = :condition AND `a`.`catid` IN (:preparedArray3) AND (`a`.`publish_up` IS NULL OR `a`.`publish_up` <= :publishUp) AND (`a`.`publish_down` IS NULL OR `a`.`publish_down` >= :publishDown) ORDER BY a.ordering ASC11.4ms576.97KBParams/libraries/src/MVC/Model/BaseDatabaseModel.php:166Copy
  • SELECT a.params FROM j4_advancedmodules AS a WHERE a.module_id = 224135μs840B/plugins/system/advancedmodules/src/Helper.php:151Copy
  • SELECT `name`,`element` FROM `j4_extensions` WHERE `type` = 'plugin' AND `folder` = 'finder' AND `enabled` = 1305μs1KB/administrator/components/com_finder/src/Helper/LanguageHelper.php:135Copy
  • SELECT `title` FROM `j4_finder_taxonomy` WHERE `parent_id` = 1 AND `state` = 1 AND `access` IN (1)259μs936B/administrator/components/com_finder/src/Indexer/Taxonomy.php:314Copy
  • SELECT a.id, a.parent_id, a.config_name, a.name, a.context, a.label, a.alias, a.display, a.state, a.access, a.root, a.ordering, a.checked_out, a.checked_out_time, a.created_time, a.updated_time, a.language,`a`.`attribs` AS `attributes` FROM `j4_jfilters_filters` AS `a` WHERE `a`.`access` IN (:preparedArray1) AND `a`.`state` IN (:preparedArray2,:preparedArray3) ORDER BY a.ordering ASC470μs4.52KBParams/libraries/src/MVC/Model/BaseDatabaseModel.php:166Copy
  • SELECT SUM(CASE WHEN `a`.`next_execution` <= :now THEN 1 ELSE 0 END) AS due_count,SUM(CASE WHEN `a`.`locked` IS NULL THEN 0 ELSE 1 END) AS locked_count FROM `j4_scheduler_tasks` AS `a` WHERE `a`.`state` = 1267μs1.68KBParams/administrator/components/com_scheduler/src/Model/TasksModel.php:466Copy
  • SELECT `session_id` FROM `j4_session` WHERE `session_id` = ?137μs1.63KBParams/libraries/vendor/joomla/session/src/Handler/DatabaseHandler.php:291Copy
  • UPDATE `j4_session` SET `data` = ? , `time` = ? WHERE `session_id` = ?206μs912BParams/libraries/vendor/joomla/session/src/Handler/DatabaseHandler.php:318Copy